Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирский Государственный Университет Телекоммуникаций и Информатики

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Механика.Методика решения задач

.pdf

Скачиваний:

Добавлен:

11.04.2015

Размер:

4.96 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 374 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Ƚɥɚɜɚ 1. Ʉɢɧɟɦɚɬɢɤɚ ɦɚɬɟɪɢɚɥɶɧɨɣ ɬɨɱɤɢ ɢ ɩɪɨɫɬɟɣɲɢɯ ɫɢɫɬɟɦ

Ⱦɥɹ ɪɟɲɟɧɢɹ ɡɚɞɚɱɢ ɡɚɩɢɫɚɧɧɵɟ ɭɪɚɜɧɟɧɢɹ ɧɟɨɛɯɨɞɢɦɨ ɞɨɩɨɥɧɢɬɶ ɨɩɪɟɞɟɥɟɧɢɹɦɢ (1.24) ɢ ɜɵɪɚɠɟɧɢɹɦɢ (1.25) ɞɥɹ ɢɧɬɟɪɟɫɭɸɳɢɯ ɧɚɫ ɜɟɥɢɱɢɧ, ɩɪɢɜɟɞɟɧɧɵɦɢ ɜ ɩ. 1.1.

III. ɇɚɣɞɟɦ ɡɚɤɨɧɵ ɢɡɦɟɧɟɧɢɹ ɫɤɨɪɨɫɬɢ ɝɪɭɡɚ ɢ ɟɝɨ ɭɫɤɨɪɟɧɢɹ ɜ ɩɪɨɟɤɰɢɹɯ ɧɚ ɨɫɢ ɞɟɤɚɪɬɨɜɨɣ ɫɢɫɬɟɦɵ ɤɨɨɪɞɢɧɚɬ, ɢɫɩɨɥɶɡɭɹ

ɨɩɪɟɞɟɥɟɧɢɹ (1.6) ɢ (1.12):
Xx	dx	2bt , Xy	0 ;	(1.82)
	dt

ax	dX	2b , ay	0 .	(1.83)
	d t

Ɍɨɱɤɢ ɨɛɨɞɚ ɜɚɥɚ ɫɨɜɟɪɲɚɸɬ ɧɟɪɚɜɧɨɦɟɪɧɨɟ ɞɜɢɠɟɧɢɟ ɩɨ ɨɤɪɭɠɧɨɫɬɢ, ɩɪɢɱɟɦ ɦɨɞɭɥɶ ɢɯ ɫɤɨɪɨɫɬɢ (ɩɨɫɤɨɥɶɤɭ ɧɢɬɶ ɧɟɪɚɫɬɹɠɢɦɚ ɢ ɧɟ ɩɪɨɫɤɚɥɶɡɵɜɚɟɬ ɩɨ ɩɨɜɟɪɯɧɨɫɬɢ ɨɛɨɞɚ) ɜ ɤɚɠɞɵɣ ɦɨɦɟɧɬ ɜɪɟɦɟɧɢ ɪɚɜɟɧ ɦɨɞɭɥɸ ɫɤɨɪɨɫɬɢ ɝɪɭɡɚ, ɩɨɷɬɨɦɭ, ɢɫɩɨɥɶɡɭɹ (1.22) ɞɥɹ ɭɝɥɨɜɨɣ ɫɤɨɪɨɫɬɢ Z ɢ ɭɝɥɨɜɨɝɨ ɭɫɤɨɪɟɧɢɹ E, ɩɨɥɭɱɚɟɦ:

Z	Xx	2bt		,		(1.84)
	R		R

E	d Z		2b		.	(1.85)
	d t
			R

ɉɨɫɤɨɥɶɤɭ ɩɪɨɟɤɰɢɹ ɭɫɤɨɪɟɧɢɹ ɝɪɭɡɚ ɧɚ ɨɫɶ X ɪɚɜɧɚ ɬɚɧɝɟɧɰɢɚɥɶɧɨɣ ɩɪɨɟɤɰɢɢ ɭɫɤɨɪɟɧɢɹ ɬɨɱɟɤ ɨɛɨɞɚ, ɬɨ:

aW	2b .									(1.86)
ɇɨɪɦɚɥɶɧɭɸ ɩɪɨɟɤɰɢɸ ɭɫɤɨɪɟɧɢɹ ɨɩɪɟɞɟɥɢɦ, ɢɫɩɨɥɶɡɭɹ
(1.22):
an	X2	4b2t		2	.					(1.87)
an	R		R		.					(1.87)
	R		R
Ɇɨɞɭɥɶ ɩɨɥɧɨɝɨ ɭɫɤɨɪɟɧɢɹ ɩɪɨɢɡɜɨɥɶɧɨɣ ɬɨɱɤɢ A ɧɚ ɨɛɨɞɟ
ɤɨɥɟɫɚ ɧɚɣɞɟɦ ɢɡ ɫɨɨɬɧɨɲɟɧɢɹ (1.20):
a	a2 a2			2b		4b2t 4		1 .		(1.88)
a	a2 a2			2b				1 .		(1.88)
	n		W			R2
						R2
Ɂɚɤɨɧ ɞɜɢɠɟɧɢɹ ɩɪɨɢɡɜɨɥɶɧɨɣ ɬɨɱɤɢ A ɧɚ ɨɛɨɞɟ ɜɚɥɚ ɡɚɩɢ-
ɲɟɦ ɜ ɩɨɥɹɪɧɨɣ ɫɢɫɬɟɦɟ ɤɨɨɪɞɢɧɚɬ:
M(t)	M0		E t 2		M0		bt 2		,	(1.89)
M(t)	M0		2		M0		R		,	(1.89)
			2				R

ɝɞɟ M0 – ɧɚɱɚɥɶɧɨɟ ɡɧɚɱɟɧɢɟ ɭɝɥɨɜɨɣ ɤɨɨɪɞɢɧɚɬɵ ɬɨɱɤɢ A ɜ ɜɵɛɪɚɧɧɨɣ ɩɨɥɹɪɧɨɣ ɫɢɫɬɟɦɟ ɤɨɨɪɞɢɧɚɬ.

32 ɆȿɏȺɇɂɄȺ. ɆȿɌɈȾɂɄȺ Ɋȿɒȿɇɂə ɁȺȾȺɑ

Ɂɚɞɚɱɚ 1.9

(ɇɚ ɤɢɧɟɦɚɬɢɤɭ ɦɚɬɟɪɢɚɥɶɧɨɣ ɬɨɱɤɢ)

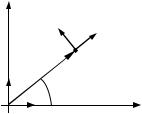
Ɂɚɤɨɧ ɞɜɢɠɟɧɢɹ ɞɜɢɠɭɳɟɣɫɹ ɜ ɩɥɨɫɤɨɫɬɢ ɦɚɬɟɪɢɚɥɶɧɨɣ ɬɨɱɤɢ, ɡɚɞɚɧɧɵɣ ɜ ɩɨɥɹɪɧɨɣ ɫɢɫɬɟɦɟ ɤɨɨɪɞɢɧɚɬ, ɢɦɟɟɬ ɫɥɟɞɭɸɳɢɣ

ɜɢɞ: r = r(t), ĳ = ĳ(t). Ɉɩɪɟɞɟɥɢɬɶ ɡɚ-
ɤɨɧɵ ɢɡɦɟɧɟɧɢɹ ɩɪɨɟɤɰɢɣ ɫɤɨɪɨɫɬɢ ɢ	Y
ɭɫɤɨɪɟɧɢɹ ɦɚɬɟɪɢɚɥɶɧɨɣ ɬɨɱɤɢ ɧɚ		eM	er
ɧɚɩɪɚɜɥɟɧɢɹ, ɡɚɞɚɜɚɟɦɵɟ ɨɪɬɚɦɢ ɞɟ-		eM	er
ɤɚɪɬɨɜɨɣ ɢ ɩɨɥɹɪɧɨɣ ɫɢɫɬɟɦ ɤɨɨɪɞɢ-		r	M
ɧɚɬ, ɠɟɫɬɤɨ ɫɜɹɡɚɧɧɵɯ ɫ ɬɟɥɨɦ ɨɬɫɱɟ-		r	M
ɧɚɬ, ɠɟɫɬɤɨ ɫɜɹɡɚɧɧɵɯ ɫ ɬɟɥɨɦ ɨɬɫɱɟ-	j
ɬɚ. ɇɚɱɚɥɨ ɞɟɤɚɪɬɨɜɨɣ ɫɢɫɬɟɦɵ ɤɨɨɪ-	j	M
ɞɢɧɚɬ ɫɨɜɩɚɞɚɟɬ ɫ ɩɨɥɸɫɨɦ ɩɨɥɹɪɧɨɣ		M
ɞɢɧɚɬ ɫɨɜɩɚɞɚɟɬ ɫ ɩɨɥɸɫɨɦ ɩɨɥɹɪɧɨɣ
ɫɢɫɬɟɦɵ, ɚ ɨɫɶ X ɞɟɤɚɪɬɨɜɨɣ ɫɢɫɬɟɦɵ	O	i	X
ɧɚɩɪɚɜɥɟɧɚ ɜɞɨɥɶ ɩɨɥɹɪɧɨɣ ɨɫɢ (ɫɦ.		Ɋɢɫ. 1.14
ɪɢɫ. 1.14).		Ɋɢɫ. 1.14
Ɋɟɲɟɧɢɟ

I. ȼɵɛɟɪɟɦ ɨɫɶ Y ɞɟɤɚɪɬɨɜɨɣ ɫɢɫɬɟɦɵ ɤɨɨɪɞɢɧɚɬ ɬɚɤ, ɱɬɨɛɵ ɩɥɨɫɤɨɫɬɶ XY ɫɨɜɩɚɞɚɥɚ ɫ ɩɥɨɫɤɨɫɬɶɸ, ɜ ɤɨɬɨɪɨɣ ɞɜɢɠɟɬɫɹ ɦɚɬɟɪɢɚɥɶɧɚɹ ɬɨɱɤɚ M (ɪɢɫ. 1.14). Ⱦɥɹ ɪɟɲɟɧɢɹ ɡɚɞɚɱɢ ɢɫɩɨɥɶɡɭɟɦ ɞɜɟ ɫɢɫɬɟɦɵ ɤɨɨɪɞɢɧɚɬ – ɞɟɤɚɪɬɨɜɭ ɫɢɫɬɟɦɭ ɤɨɨɪɞɢɧɚɬ XOY c ɨɪɬɚɦɢ i ɢ j , ɢ ɩɨɥɹɪɧɭɸ, ɨɪɬɵ ɤɨɬɨɪɨɣ er ɢ eM ɢɡɨɛɪɚɠɟɧɵ ɧɚ ɪɢɫ. 1.14.

Ɂɚɦɟɬɢɦ, ɱɬɨ ɩɪɢ ɞɜɢɠɟɧɢɢ ɦɚɬɟɪɢɚɥɶɧɨɣ ɬɨɱɤɢ ɩɪɨɢɫɯɨɞɢɬ ɢɡɦɟɧɟɧɢɟ ɨɪɢɟɧɬɚɰɢɢ ɨɪɬɨɜ ɩɨɥɹɪɧɨɣ ɫɢɫɬɟɦɵ er ɢ eM , ɜ ɬɨ ɜɪɟɦɹ ɤɚɤ

ɨɪɬɵ ɞɟɤɚɪɬɨɜɨɣ ɫɢɫɬɟɦɵ ɤɨɨɪɞɢɧɚɬ i ɢ j ɧɟ ɢɡɦɟɧɹɸɬ ɫɜɨɟɝɨ ɧɚ-

ɩɪɚɜɥɟɧɢɹ.

II, III. Ɂɚɤɨɧ ɞɜɢɠɟɧɢɹ ɦɚɬɟɪɢɚɥɶɧɨɣ ɬɨɱɤɢ, ɡɚɞɚɧɧɵɣ ɜ ɩɨɥɹɪɧɨɣ ɫɢɫɬɟɦɟ, ɡɚɩɢɲɟɦ ɜ ɞɟɤɚɪɬɨɜɨɣ ɫɢɫɬɟɦɟ ɤɨɨɪɞɢɧɚɬ XOY:

x(t) r(t) cosM(t),

(1.90)

y(t) r(t)sinM(t).

Ⱦɢɮɮɟɪɟɧɰɢɪɭɹ ɡɚɤɨɧ ɞɜɢɠɟɧɢɹ (1.90) ɩɨ ɜɪɟɦɟɧɢ, ɩɨɥɭɱɚɟɦ ɢɫɤɨɦɵɟ ɡɚɤɨɧɵ ɢɡɦɟɧɟɧɢɹ ɩɪɨɟɤɰɢɣ ɫɤɨɪɨɫɬɢ ɦɚɬɟɪɢɚɥɶɧɨɣ ɬɨɱɤɢ

ɢ ɟɟ ɭɫɤɨɪɟɧɢɹ ɜ ɞɟɤɚɪɬɨɜɨɣ ɫɢɫɬɟɦɟ ɤɨɨɪɞɢɧɚɬ:
Xx
	x	r cosM rM sinM,	(1.91)
X y
	y	r sinM rM cosM;

Ƚɥɚɜɚ 1. Ʉɢɧɟɦɚɬɢɤɚ ɦɚɬɟɪɢɚɥɶɧɨɣ ɬɨɱɤɢ ɢ ɩɪɨɫɬɟɣɲɢɯ ɫɢɫɬɟɦ						33
ax			2
ax	Xx	(r	rM	) cosM (2rM	rM) sinM,	(1.92)
a y			2			(1.92)
			2
	X y	(r	rM	) sinM (2rM	rM) cosM.

ȼ ɮɨɪɦɭɥɚɯ (1.92), (1.92) ɢ ɞɚɥɟɟ ɞɥɹ ɤɪɚɬɤɨɫɬɢ ɨɩɭɫɬɢɦ ɡɚɩɢɫɶ ɡɚɜɢɫɢɦɨɫɬɢ ɤɢɧɟɦɚɬɢɱɟɫɤɢɯ ɜɟɥɢɱɢɧ ɨɬ ɜɪɟɦɟɧɢ.

ɉɪɨɟɤɰɢɢ ɫɤɨɪɨɫɬɢ ɢ ɭɫɤɨɪɟɧɢɹ ɦɚɬɟɪɢɚɥɶɧɨɣ ɬɨɱɤɢ ɜ ɩɨɥɹɪɧɨɣ ɫɢɫɬɟɦɟ ɤɨɨɪɞɢɧɚɬ ɧɚɯɨɞɢɦ ɞɜɭɦɹ ɫɩɨɫɨɛɚɦɢ.

1 ɫɩɨɫɨɛ. ɋɤɨɪɨɫɬɶ ɢ ɭɫɤɨɪɟɧɢɟ ɦɚɬɟɪɢɚɥɶɧɨɣ ɬɨɱɤɢ ɜ ɩɨɥɹɪ-

ɧɨɣ ɫɢɫɬɟɦɟ ɤɨɨɪɞɢɧɚɬ ɡɚɩɢɫɵɜɚɸɬɫɹ ɜ ɜɢɞɟ:
ȣ	Xr er XMeM ,	(1.93)
a	ar er aMeM .	(1.94)

ɋɥɟɞɨɜɚɬɟɥɶɧɨ, ɩɪɨɟɤɰɢɢ ɫɤɨɪɨɫɬɢ ɢ ɭɫɤɨɪɟɧɢɹ ɦɚɬɟɪɢɚɥɶɧɨɣ ɬɨɱɤɢ ɧɚ ɧɚɩɪɚɜɥɟɧɢɹ, ɡɚɞɚɜɚɟɦɵɟ ɨɪɬɚɦɢ ɪɚɫɫɦɚɬɪɢɜɚɟɦɵɯ ɫɢɫɬɟɦ ɤɨɨɪɞɢɧɚɬ, ɫɜɹɡɚɧɵ ɫɨɨɬɧɨɲɟɧɢɹɦɢ:

Xx	ȣ i	Xr er i XM eM i	Xr cosM XM sin M,	(1.95)
Xy	ȣ j	Xr er j XM eM j	Xr sin M XM cosM;

ax	a i	ar er i aM eM i	ar cosM aM sinM,	(1.96)
ay	a j	ar er j aMeM j	ar sin M aM cosM.

ɋɪɚɜɧɢɜɚɹ ɫɨɨɬɧɨɲɟɧɢɹ (1.90) ɢ (1.95), ɚ ɬɚɤɠɟ (1.91) ɢ (1.96), ɩɨɥɭɱɢɦ ɢɫɤɨɦɵɟ ɩɪɨɟɤɰɢɢ ɫɤɨɪɨɫɬɢ ɢ ɭɫɤɨɪɟɧɢɹ ɦɚɬɟɪɢɚɥɶɧɨɣ ɬɨɱɤɢ ɜ ɩɨɥɹɪɧɨɣ ɫɢɫɬɟɦɟ ɤɨɨɪɞɢɧɚɬ:

Xr
Xr	r,			(1.97)
XM				(1.97)
XM	rM;
ar		2	,
ar	r rM		,	(1.98)
aM				(1.98)
aM	2rM	rM.

2 ɫɩɨɫɨɛ. Ɂɚɩɢɲɟɦ ɪɚɞɢɭɫ-ɜɟɤɬɨɪ ɦɚɬɟɪɢɚɥɶɧɨɣ ɬɨɱɤɢ ɜ ɩɨɥɹɪɧɨɣ ɫɢɫɬɟɦɟ ɤɨɨɪɞɢɧɚɬ:

r rer .

(1.99)

ɉɨɫɤɨɥɶɤɭ ɩɪɢ ɞɜɢɠɟɧɢɢ ɦɚɬɟɪɢɚɥɶɧɨɣ ɬɨɱɤɢ ɩɪɨɢɫɯɨɞɢɬ ɢɡɦɟɧɟɧɢɟ ɨɪɢɟɧɬɚɰɢɢ ɨɪɬɨɜ ɩɨɥɹɪɧɨɣ ɫɢɫɬɟɦɵ er ɢ eM , ɧɚɣɞɟɦ

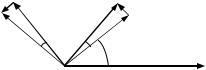
ɫɤɨɪɨɫɬɶ ɢɯ ɢɡɦɟɧɟɧɢɹ (ɫɦ. ɪɢɫ. 1.15):


er	MeM ,	(1.100)
		(1.100)
eM	Mer.

34 ɆȿɏȺɇɂɄȺ. ɆȿɌɈȾɂɄȺ Ɋȿɒȿɇɂə ɁȺȾȺɑ

deM	e	der
	e	der
	dM	r
	dM
	dM
	O	X
		Ɋɢɫ. 1.15

Ɍɟɩɟɪɶ ɞɥɹ ɧɚɯɨɠɞɟɧɢɹ ɫɤɨɪɨɫɬɢ ɢ ɭɫɤɨɪɟɧɢɹ ɬɨɱɤɢ ɜ ɬɨɣ ɠɟ ɫɢɫɬɟɦɟ ɤɨɨɪɞɢɧɚɬ ɧɟɨɛɯɨɞɢɦɨ ɩɪɨɞɢɮɮɟɪɟɧɰɢɪɨɜɚɬɶ ɪɚɞɢɭɫɜɟɤɬɨɪ (1.99) ɩɨ ɜɪɟɦɟɧɢ ɫ ɭɱɟɬɨɦ (1.100):

							,	(1.101)
ȣ r	rer	rer		rer	rMeM		,	(1.101)

a ȣ	rer	rer		rMeM rMeM rMeM
	2		)er					(1.102)
(r	rM		)er	(2rM		rM)eM .		(1.102)

ȼ ɫɨɨɬɜɟɬɫɬɜɢɢ ɫ (1.101) ɢ (1.102) ɢɫɤɨɦɵɟ ɩɪɨɟɤɰɢɢ ɫɤɨɪɨɫɬɢ ɢ ɭɫɤɨɪɟɧɢɹ ɦɚɬɟɪɢɚɥɶɧɨɣ ɬɨɱɤɢ ɜ ɩɨɥɹɪɧɨɣ ɫɢɫɬɟɦɟ ɤɨɨɪɞɢɧɚɬ ɪɚɜɧɵ:

Xr
	r,			(1.103)
XM		;
	rM
ar		2
	r rM		,	(1.104)
aM
	2rM rM.

Ʉɚɤ ɜɢɞɢɦ, ɨɛɚ ɫɩɨɫɨɛɚ ɪɟɲɟɧɢɹ ɞɚɸɬ ɨɞɢɧɚɤɨɜɵɣ ɪɟɡɭɥɶɬɚɬ.

Ɂɚɞɚɱɚ 1.10

(ɇɚ ɤɢɧɟɦɚɬɢɤɭ ɦɚɬɟɪɢɚɥɶɧɨɣ ɬɨɱɤɢ)

Ⱦɜɢɠɟɧɢɟ ɦɚɬɟɪɢɚɥɶɧɨɣ ɬɨɱɤɢ ɜ ɩɨɥɹɪɧɨɣ ɫɢɫɬɟɦɟ ɤɨɨɪɞɢɧɚɬ ɡɚɞɚɟɬɫɹ ɜɡɚɢɦɨɫɜɹɡɶɸ ɩɨɥɹɪɧɵɯ ɤɨɨɪɞɢɧɚɬ r(M) 2a(1 cosM) , ɩɪɢ ɷɬɨɦ ɩɨɥɹɪɧɵɣ ɭɝɨɥ ɜɨɡɪɚɫɬɚɟɬ ɥɢɧɟɣɧɨ ɜɨ

ɜɪɟɦɟɧɢ M(t) bt . Ɉɩɪɟɞɟɥɢɬɶ ɡɚɜɢɫɢɦɨɫɬɶ ɦɨɞɭɥɹ ɫɤɨɪɨɫɬɢ ɢ ɦɨɞɭɥɹ ɭɫɤɨɪɟɧɢɹ ɦɚɬɟɪɢɚɥɶɧɨɣ ɬɨɱɤɢ ɨɬ ɜɪɟɦɟɧɢ.

Ɋɟɲɟɧɢɟ

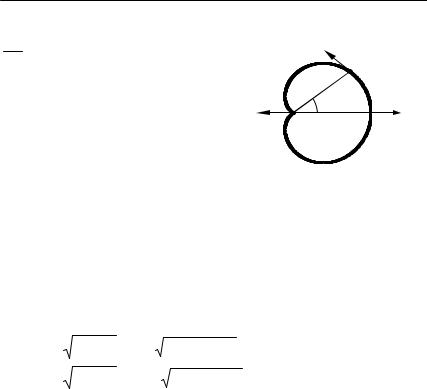
I. Ɋɟɲɚɟɦ ɡɚɞɚɱɭ ɜ ɡɚɞɚɧɧɨɣ ɩɨɥɹɪɧɨɣ ɫɢɫɬɟɦɟ ɤɨɨɪɞɢɧɚɬ. Ɂɚɦɟɬɢɦ, ɱɬɨ ɦɚɬɟɪɢɚɥɶɧɚɹ ɬɨɱɤɚ M ɞɜɢɠɟɬɫɹ ɩɨ ɡɚɦɤɧɭɬɨɣ ɬɪɚɟɤ-

Ƚɥɚɜɚ 1. Ʉɢɧɟɦɚɬɢɤɚ ɦɚɬɟɪɢɚɥɶɧɨɣ ɬɨɱɤɢ ɢ ɩɪɨɫɬɟɣɲɢɯ ɫɢɫɬɟɦ										35
ɬɨɪɢɢ, ɩɟɪɢɨɞɢɱɟɫɤɢ, ɫ ɩɟɪɢɨɞɨɦ
2S									ȣ(t)
b , ɜɨɡɜɪɚɳɚɹɫɶ ɜ ɬɭ				ɠɟ			ɬɨɱɤɭ
									M
ɩɪɨɫɬɪɚɧɫɬɜɚ (ɫɦ. ɪɢɫ. 1.16).								a(tk )	r(t)
II. Ɉɩɪɟɞɟɥɢɦ ɡɚɤɨɧ ɢɡɦɟɧɟ-									M(t)
ɧɢɹ ɩɪɨɟɤɰɢɣ ɫɤɨɪɨɫɬɢ ɢ ɭɫɤɨɪɟ-									O	X
ɧɢɹ ɦɚɬɟɪɢɚɥɶɧɨɣ ɬɨɱɤɢ ɜ ɩɨɥɹɪ-
ɧɨɣ ɫɢɫɬɟɦɟ ɤɨɨɪɞɢɧɚɬ, ɜɨɫɩɨɥɶ-
ɡɨɜɚɜɲɢɫɶ	ɮɨɪɦɭɥɚɦɢ			(1.103) ɢ
(1.104), ɩɨɥɭɱɟɧɧɵɦɢ ɜ ɩɪɟɞɵɞɭ-									Ɋɢɫ. 1.16
ɳɟɣ ɡɚɞɚɱɟ:		2a sinMM			2ab sinM,
Xr	r
										(1.105)
XM		2a(1 cosM)b;
	rM
ar		2	2ab	2	(2 cosM 1),
	r rM									(1.106)
aM			4ab			2	sinM.

	2rM rM

Ɍɨɝɞɚ ɢɫɤɨɦɵɟ ɦɨɞɭɥɢ ɫɤɨɪɨɫɬɢ ɢ ɭɫɤɨɪɟɧɢɹ ɦɚɬɟɪɢɚɥɶɧɨɣ ɬɨɱɤɢ ɪɚɜɧɵ:

X	X2	X2	2ab	2 2 cos(bt) ,	(1.107)
	r	M
a	a2	a2	2ab2	5 4 cos(bt).	(1.108)
	r	M

	Ɂɚɦɟɬɢɦ, ɱɬɨ ɦɚɬɟɪɢɚɥɶɧɚɹ ɬɨɱɤɚ ɜ ɦɨɦɟɧɬɵ ɜɪɟɦɟɧɢ
tk	(2k 1) S	(ɝɞɟ k = 0, 1, 2, ...) ɧɚɯɨɞɢɬɫɹ ɜ ɧɚɱɚɥɟ (ɩɨɥɸɫɟ) ɩɨ-
	b

ɥɹɪɧɨɣ ɫɢɫɬɟɦɵ ɤɨɨɪɞɢɧɚɬ, ɢɦɟɟɬ ɧɭɥɟɜɭɸ ɫɤɨɪɨɫɬɶ, ɚ ɭɫɤɨɪɟɧɢɟ, ɩɨ ɦɨɞɭɥɸ ɪɚɜɧɨɟ a(tk ) 2ab2 , ɧɚɩɪɚɜɥɟɧɨ ɩɪɨɬɢɜɨɩɨɥɨɠɧɨ ɩɨɥɹɪɧɨɣ ɨɫɢ.

Ɂɚɞɚɱɚ 1.11

(ɇɚ ɤɢɧɟɦɚɬɢɤɭ ɦɚɬɟɪɢɚɥɶɧɨɣ ɬɨɱɤɢ)

ɉɥɚɧɟɬɚ ɞɜɢɠɟɬɫɹ ɜɨɤɪɭɝ ɋɨɥɧɰɚ ɜ ɫɨɨɬɜɟɬɫɬɜɢɢ ɫ ɡɚɤɨɧɚɦɢ Ʉɟɩɥɟɪɚ ɩɨ ɷɥɥɢɩɬɢɱɟɫɤɨɣ ɬɪɚɟɤɬɨɪɢɢ r(1 e cosM) p . ɉɚɪɚɦɟɬɪ

ɷɥɥɢɩɫɚ p , ɷɤɫɰɟɧɬɪɢɫɢɬɟɬ e ɢ ɫɟɤɬɨɪɧɭɸ ɫɤɨɪɨɫɬɶ V ɫɱɢɬɚɬɶ ɡɚ-

ɞɚɧɧɵɦɢ. Ɉɩɪɟɞɟɥɢɬɶ ɩɪɨɟɤɰɢɢ ɭɫɤɨɪɟɧɢɹ ɩɥɚɧɟɬɵ ɜ ɡɚɜɢɫɢɦɨɫɬɢ ɨɬ ɤɨɨɪɞɢɧɚɬ r ɢ M ɩɨɥɹɪɧɨɣ ɫɢɫɬɟɦɵ.

36	ɆȿɏȺɇɂɄȺ. ɆȿɌɈȾɂɄȺ Ɋȿɒȿɇɂə ɁȺȾȺɑ

Ɋɟɲɟɧɢɟ

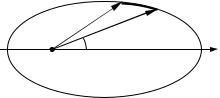
I. ɉɪɢ ɪɟɲɟɧɢɢ ɡɚɞɚɱɢ ɛɭɞɟɦ ɫɱɢɬɚɬɶ ɩɥɚɧɟɬɭ ɢ ɋɨɥɧɰɟ ɦɚɬɟɪɢɚɥɶɧɵɦɢ ɬɨɱɤɚɦɢ. ɋɨɝɥɚɫɧɨ ɩɟɪɜɨɦɭ ɡɚɤɨɧɭ Ʉɟɩɥɟɪɚ ɜɫɟ ɩɥɚɧɟɬɵ ɞɜɢɠɭɬɫɹ ɩɨ ɷɥɥɢɩɬɢɱɟɫɤɢɦ ɨɪɛɢɬɚɦ, ɩɪɢɱɟɦ ɋɨɥɧɰɟ ɧɚɯɨɞɢɬɫɹ ɜ ɨɞɧɨɦ ɢɡ ɮɨɤɭɫɨɜ ɷɥɥɢɩɫɚ O (ɫɦ. ɪɢɫ. 1.17).

		rM't

	r(t+ǻt)	r(t)
	M(t)	r(t)
	M(t)
	O	X
	Ɋɢɫ. 1.17

ȼ ɫɨɨɬɜɟɬɫɬɜɢɢ ɫ ɭɫɥɨɜɢɟɦ ɡɚɞɚɱɢ ɜɜɟɞɟɦ ɩɨɥɹɪɧɭɸ ɫɢɫɬɟɦɭ ɤɨɨɪɞɢɧɚɬ ɜ ɩɥɨɫɤɨɫɬɢ ɞɜɢɠɟɧɢɹ ɩɥɚɧɟɬɵ, ɩɨɥɸɫ ɤɨɬɨɪɨɣ ɫɨɜɩɚɞɚɟɬ ɫ ɋɨɥɧɰɟɦ, ɚ ɩɨɥɹɪɧɚɹ ɨɫɶ ɫɨɜɩɚɞɚɟɬ ɫ ɨɞɧɨɣ ɢɡ ɨɫɟɣ ɷɥɥɢɩɫɚ.

ɋɨɝɥɚɫɧɨ ɜɬɨɪɨɦɭ ɡɚɤɨɧɭ Ʉɟɩɥɟɪɚ ɫɟɤɬɨɪɧɚɹ ɫɤɨɪɨɫɬɶ V ɩɥɚɧɟɬɵ, ɪɚɜɧɚɹ ɫɤɨɪɨɫɬɢ ɢɡɦɟɧɟɧɢɹ ɩɥɨɳɚɞɢ, ɨɩɢɫɵɜɚɟɦɨɣ ɪɚɞɢ- ɭɫ-ɜɟɤɬɨɪɨɦ ɦɚɬɟɪɢɚɥɶɧɨɣ ɬɨɱɤɢ, ɩɪɟɞɫɬɚɜɥɹɸɳɢɦ ɩɥɚɧɟɬɭ, ɩɨɫɬɨɹɧɧɚ ɩɪɢ ɞɜɢɠɟɧɢɢ ɩɥɚɧɟɬɵ ɜɨɤɪɭɝ ɋɨɥɧɰɚ.

II. Ⱦɥɹ ɧɚɯɨɠɞɟɧɢɹ ɩɪɨɟɤɰɢɣ ɭɫɤɨɪɟɧɢɹ ɩɥɚɧɟɬɵ ɜ ɩɨɥɹɪɧɨɣ

ɫɢɫɬɟɦɟ ɤɨɨɪɞɢɧɚɬ ɜɨɫɩɨɥɶɡɭɟɦɫɹ ɮɨɪɦɭɥɚɦɢ (1.104):
ar		2	,
	r rM			(1.109)
aM
	2rM	rM.

ɉɨɫɤɨɥɶɤɭ ɜ ɭɪɚɜɧɟɧɢɹ (1.109) ɜɯɨɞɹɬ ɩɪɨɢɡɜɨɞɧɵɟ ɩɨɥɹɪɧɵɯ ɤɨɨɪɞɢɧɚɬ ɩɨ ɜɪɟɦɟɧɢ, ɞɨɩɨɥɧɢɦ ɷɬɭ ɫɢɫɬɟɦɭ ɭɪɚɜɧɟɧɢɟɦ ɬɪɚɟɤɬɨɪɢɢ ɩɥɚɧɟɬɵ ɢ ɜɵɪɚɠɟɧɢɟɦ ɞɥɹ ɟɟ ɫɟɤɬɨɪɧɨɣ ɫɤɨɪɨɫɬɢ V :

r(1 e cosM) p ,			(1.110)
V	1	2	(1.111)

	2 r M .

III. ȼ ɫɨɨɬɜɟɬɫɬɜɢɢ ɫ ɭɫɥɨɜɢɟɦ ɡɚɞɚɱɢ ɫɟɤɬɨɪɧɚɹ ɫɤɨɪɨɫɬɶ V ɩɨɫɬɨɹɧɧɚ ɩɪɢ ɞɜɢɠɟɧɢɢ ɩɥɚɧɟɬɵ ɩɨ ɷɥɥɢɩɬɢɱɟɫɤɨɣ ɬɪɚɟɤɬɨɪɢɢ, ɩɨɷɬɨɦɭ ɟɟ ɩɪɨɢɡɜɨɞɧɚɹ ɩɨ ɜɪɟɦɟɧɢ ɪɚɜɧɚ ɧɭɥɸ:

Ƚɥɚɜɚ 1. Ʉɢɧɟɦɚɬɢɤɚ ɦɚɬɟɪɢɚɥɶɧɨɣ ɬɨɱɤɢ ɢ ɩɪɨɫɬɟɣɲɢɯ ɫɢɫɬɟɦ						37
		1	2
		2 r		0 .		(1.112)
V	rM		M
ɋɪɚɜɧɢɜɚɹ (1.112) ɫ ɜɵɪɚɠɟɧɢɟɦ (1.109)					ɞɥɹ ɩɪɨɟɤɰɢɢ ɭɫɤɨ-
ɪɟɧɢɹ aM ,	ɜɢɞɢɦ,		ɱɬɨ	aM 0 . ɋɥɟɞɨɜɚɬɟɥɶɧɨ,	ɭɫɤɨɪɟɧɢɟ ɜ ɥɸɛɨɣ

ɦɨɦɟɧɬ ɜɪɟɦɟɧɢ ɢɦɟɟɬ ɬɨɥɶɤɨ ɩɪɨɟɤɰɢɸ ar , ɤɨɬɨɪɚɹ ɜ ɫɨɨɬɜɟɬɫɬ-

ɜɢɢ ɫ (1.109) ɹɜɥɹɟɬɫɹ ɮɭɧɤɰɢɟɣ ɩɪɨɢɡɜɨɞɧɵɯ ɩɨɥɹɪɧɵɯ ɤɨɨɪɞɢɧɚɬ ɩɨ ɜɪɟɦɟɧɢ.

ɉɪɨɞɢɮɮɟɪɟɧɰɢɪɭɟɦ ɨɛɟ ɱɚɫɬɢ ɭɪɚɜɧɟɧɢɹ ɬɪɚɟɤɬɨɪɢɢ (1.110)

ɩɨ ɜɪɟɦɟɧɢ:				(1.113)

r(1	e cosM) re sinM M		0 .
ɂɫɩɨɥɶɡɭɹ ɭɪɚɜɧɟɧɢɟ ɬɪɚɟɤɬɨɪɢɢ (1.110) ɢ ɜɵɪɚɠɟɧɢɟ ɞɥɹ
ɫɟɤɬɨɪɧɨɣ ɫɤɨɪɨɫɬɢ (1.111), ɩɪɟɨɛɪɚɡɭɟɦ (1.113) ɤ ɜɢɞɭ:
		0 .		(1.114)
rp 2Ve sinM
ɉɪɨɞɢɮɮɟɪɟɧɰɢɪɭɟɦ ɬɟɩɟɪɶ ɨɛɟ ɱɚɫɬɢ ɭɪɚɜɧɟɧɢɹ (1.114) ɩɨ
ɜɪɟɦɟɧɢ		0 .		(1.115)

r p 2Ve cosM M

Ɉɩɹɬɶ ɜɨɫɩɨɥɶɡɭɟɦɫɹ ɭɪɚɜɧɟɧɢɟɦ ɬɪɚɟɤɬɨɪɢɢ (1.110) ɢ ɜɵɪɚɠɟɧɢɟɦ ɞɥɹ ɫɟɤɬɨɪɧɨɣ ɫɤɨɪɨɫɬɢ (1.111) ɞɥɹ ɢɫɤɥɸɱɟɧɢɹ cosM ɢ M

ɢɡ (1.115):	r p		2V		2 r p


	er	r 2				r3	0 .	(1.116)
rp 2Ve				rp 4V

ȼ ɪɟɡɭɥɶɬɚɬɟ ɧɚɯɨɞɢɦ:

r 4V 2 r p . (1.117) r3 p

Ⱦɥɹ ɧɚɯɨɠɞɟɧɢɹ ɢɫɤɨɦɨɣ ɩɪɨɟɤɰɢɢ ɭɫɤɨɪɟɧɢɹ ɩɥɚɧɟɬɵ ar , ɤɚɤ ɮɭɧɤɰɢɢ ɬɨɥɶɤɨ ɤɨɨɪɞɢɧɚɬ ɩɨɥɹɪɧɨɣ ɫɢɫɬɟɦɵ, ɩɨɞɫɬɚɜɢɦ r

(ɫɦ. (1.111)) ɜ ɜɵɪɚɠɟɧɢɟ (1.109):

r 2

(1.116) ɢ M

2 r p

4V 2

r3 p

r 4

r 2 p .

(1.118)

ar r

Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɭɫɤɨɪɟɧɢɟ ɩɥɚɧɟɬɵ, ɞɜɢɠɭɳɟɣɫɹ ɩɨ ɷɥɥɢɩɬɢɱɟɫɤɨɣ ɬɪɚɟɤɬɨɪɢɢ, ɧɚɩɪɚɜɥɟɧɨ ɤ ɋɨɥɧɰɭ, ɧɟ ɡɚɜɢɫɢɬ ɨɬ ɩɨɥɹɪɧɨɝɨ ɭɝɥɚ M ɢ ɨɛɪɚɬɧɨ ɩɪɨɩɨɪɰɢɨɧɚɥɶɧɨ ɤɜɚɞɪɚɬɭ ɪɚɫɫɬɨɹɧɢɹ ɞɨ ɋɨɥɧ-

ɰɚ:

38				ɆȿɏȺɇɂɄȺ. ɆȿɌɈȾɂɄȺ Ɋȿɒȿɇɂə ɁȺȾȺɑ
ar		4V 2		,
		r	2p
				(1.119)
aM	0.

Ɂɚɞɚɱɚ 1.12

(ɇɚ ɤɢɧɟɦɚɬɢɤɭ ɦɚɬɟɪɢɚɥɶɧɨɣ ɬɨɱɤɢ)

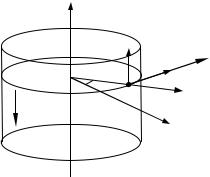
ɇɟɛɨɥɶɲɨɟ ɬɟɥɨ ɞɜɢɠɟɬɫɹ ɩɨ ɝɥɚɞɤɨɣ ɜɧɭɬɪɟɧɧɟɣ ɩɨɜɟɪɯɧɨɫɬɢ ɩɨɥɨɝɨ ɜɟɪɬɢɤɚɥɶɧɨɝɨ ɰɢɥɢɧɞɪɚ ɪɚɞɢɭɫɚ R. ȼ ɧɚɱɚɥɶɧɵɣ ɦɨɦɟɧɬ ɜɪɟɦɟɧɢ ɫɤɨɪɨɫɬɶ ɬɟɥɚ ɧɚɩɪɚɜɥɟɧɚ ɩɟɪɩɟɧɞɢɤɭɥɹɪɧɨ ɨɫɢ ɰɢɥɢɧɞɪɚ ɢ ɪɚɜɧɚ ȣ0 . Ɉɩɪɟɞɟɥɢɬɶ ɡɚɤɨɧɵ ɢɡɦɟɧɟɧɢɹ ɫɤɨɪɨɫɬɢ ɢ ɭɫɤɨ-

ɪɟɧɢɹ ɦɚɬɟɪɢɚɥɶɧɨɣ ɬɨɱɤɢ ɜ ɰɢɥɢɧɞɪɢɱɟɫɤɨɣ ɫɢɫɬɟɦɟ ɤɨɨɪɞɢɧɚɬ, ɚ ɬɚɤɠɟ ɭɝɨɥ D(t) ɦɟɠɞɭ ɫɤɨɪɨɫɬɶɸ ɢ ɭɫɤɨɪɟɧɢɟɦ.

Ɋɟɲɟɧɢɟ

I. Ȼɭɞɟɦ ɫɱɢɬɚɬɶ ɬɟɥɨ ɦɚɬɟɪɢɚɥɶɧɨɣ ɬɨɱɤɨɣ, ɤɨɬɨɪɚɹ ɞɜɢɠɟɬɫɹ ɩɨ ɰɢɥɢɧɞɪɢɱɟɫɤɨɣ ɩɨɜɟɪɯɧɨɫɬɢ ɫ ɩɨɫɬɨɹɧɧɨɣ ɜɟɪɬɢɤɚɥɶɧɨɣ ɫɨɫɬɚɜɥɹɸɳɟɣ ɭɫɤɨɪɟɧɢɹ, ɪɚɜɧɨɣ ɭɫɤɨɪɟɧɢɸ ɫɜɨɛɨɞɧɨɝɨ ɩɚɞɟɧɢɹ g .

Ⱦɥɹ ɪɟɲɟɧɢɹ ɡɚɞɚɱɢ ɜɵɛɟɪɟɦ ɰɢɥɢɧɞɪɢɱɟɫɤɭɸ ɫɢɫɬɟɦɭ ɤɨɨɪɞɢɧɚɬ, ɨɫɶ Z ɤɨɬɨɪɨɣ ɫɨɜɩɚɞɚɟɬ ɫ ɨɫɶɸ ɰɢɥɢɧɞɪɚ, ɤɚɤ ɩɨɤɚɡɚɧɨ ɧɚ ɪɢɫ. 1.18. ɇɚ ɬɨɦ ɠɟ ɪɢɫɭɧɤɟ ɢɡɨɛɪɚɠɟɧɵ ɨɪɬɵ er, eM ɢ ez ɰɢɥɢɧɞɪɢɱɟɫɤɨɣ ɫɢɫɬɟɦɵ. Ɉɫɶ, ɨɬ ɤɨɬɨɪɨɣ ɨɬɫɱɢɬɵɜɚɟɬɫɹ ɭɝɨɥ M ɫɢɫɬɟɦɵ

ɤɨɨɪɞɢɧɚɬ, ɧɚɩɪɚɜɢɦ ɧɚ ɩɨɥɨɠɟɧɢɟ ɬɟɥɚ ɜ ɧɚɱɚɥɶɧɵɣ ɦɨɦɟɧɬ ɜɪɟɦɟɧɢ.

Z
	ez	eM
O	M	eM	ȣ0
	M		ȣ0

g		r
		X
Ɋɢɫ. 1.18

Ƚɥɚɜɚ 1. Ʉɢɧɟɦɚɬɢɤɚ ɦɚɬɟɪɢɚɥɶɧɨɣ ɬɨɱɤɢ ɢ ɩɪɨɫɬɟɣɲɢɯ ɫɢɫɬɟɦ

II. ȼ ɫɨɨɬɜɟɬɫɬɜɢɢ ɫ ɭɫɥɨɜɢɹɦɢ ɡɚɞɚɱɢ ɢ ɜɵɛɪɚɧɧɨɣ ɫɢɫɬɟɦɨɣ ɤɨɨɪɞɢɧɚɬ ɡɚɩɢɲɟɦ ɧɚɱɚɥɶɧɵɟ ɡɧɚɱɟɧɢɹ ɩɪɨɟɤɰɢɣ ɫɤɨɪɨɫɬɢ ɞɥɹ

ɪɚɫɫɦɚɬɪɢɜɚɟɦɨɝɨ ɬɟɥɚ:
Xr (0) 0 , XM (0) X0 , Xz (0) 0 .	(1.120)

ȼɨɫɩɨɥɶɡɭɟɦɫɹ ɮɨɪɦɭɥɚɦɢ (1.103) ɢ (1.104) ɞɥɹ ɩɪɨɟɤɰɢɣ ɫɤɨɪɨɫɬɢ ɢ ɭɫɤɨɪɟɧɢɹ ɬɟɥɚ ɧɚ ɧɚɩɪɚɜɥɟɧɢɹ, ɡɚɞɚɜɚɟɦɵɟ ɨɪɬɚɦɢ ɰɢ-

ɥɢɧɞɪɢɱɟɫɤɨɣ ɫɢɫɬɟɦɵ:
ȣr			ȣM			ȣz					(1.121)
		r ,			rM ,		z ,
ar				2	, aM						(1.122)
		r rM				2rM rM , az				z .
Ʉɪɨɦɟ ɬɨɝɨ, ɜ ɫɨɨɬɜɟɬɫɬɜɢɢ ɫ ɭɫɥɨɜɢɹɦɢ ɡɚɞɚɱɢ, ɡɚɩɢɲɟɦ:
r(t) R ,				aM (t)		0 , az (t)			g .		(1.123)
III. ɂɫɩɨɥɶɡɭɹ (1.121) – (1.123),										ɩɨɥɭɱɢɦ ɡɚɤɨɧɵ ɢɡɦɟɧɟɧɢɹ
ɩɪɨɟɤɰɢɣ ɫɤɨɪɨɫɬɢ ɢ ɭɫɤɨɪɟɧɢɹ:
Xr (t)			0 , XM (t)			X0 , Xz (t) gt ;					(1.124)
a		(t)		X2	, a	(t)	0 , a		(t) g .		(1.125)
	r			0				z
				R	M

Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɢɫɤɨɦɵɣ ɡɚɤɨɧ ɢɡɦɟɧɟɧɢɹ ɫɤɨɪɨɫɬɢ ɢ ɭɫɤɨɪɟɧɢɹ ɜ ɰɢɥɢɧɞɪɢɱɟɫɤɨɣ ɫɢɫɬɟɦɟ ɤɨɨɪɞɢɧɚɬ ɢɦɟɟɬ ɫɥɟɞɭɸɳɢɣ ɜɢɞ:

ȣ	X0eM gtez ,			(1.126)
a		X2	er gez .	(1.127)
		0
		R

Ɉɩɪɟɞɟɥɢɦ ɬɚɤɠɟ ɢɫɤɨɦɵɣ ɭɝɨɥ D ɦɟɠɞɭ ɫɤɨɪɨɫɬɶɸ ɢ ɭɫɤɨɪɟɧɢɟɦ ɬɟɥɚ:

cosD

ȣ a

g 2t

(1.128)

2 ¨

§X0

2 ¸

1.4. Ɂɚɞɚɱɢ ɞɥɹ ɫɚɦɨɫɬɨɹɬɟɥɶɧɨɝɨ ɪɟɲɟɧɢɹ

Ɂɚɞɚɱɚ 1

ɂɡ ɩɭɲɤɢ, ɧɚɯɨɞɹɳɟɣɫɹ ɧɚ ɫɚɦɨɥɟɬɟ, ɥɟɬɹɳɟɦ ɝɨɪɢɡɨɧɬɚɥɶɧɨ ɫɨ ɫɤɨɪɨɫɬɶɸ Xɫɚɦ , ɜɵɩɭɳɟɧ ɫɧɚɪɹɞ ɜ ɧɚɩɪɚɜɥɟɧɢɢ ɞɜɢɠɟɧɢɹ ɫɚɦɨ-

40	ɆȿɏȺɇɂɄȺ. ɆȿɌɈȾɂɄȺ Ɋȿɒȿɇɂə ɁȺȾȺɑ

ɥɟɬɚ. ɋɤɨɪɨɫɬɶ ɫɧɚɪɹɞɚ ɨɬɧɨɫɢɬɟɥɶɧɨ ɫɚɦɨɥɟɬɚ ɪɚɜɧɚ Xɫɧ . ɉɪɟɧɟɛ-

ɪɟɝɚɹ ɫɨɩɪɨɬɢɜɥɟɧɢɟɦ ɜɨɡɞɭɯɚ, ɧɚɣɬɢ:

1) ɭɪɚɜɧɟɧɢɟ ɬɪɚɟɤɬɨɪɢɢ ɫɧɚɪɹɞɚ ɨɬɧɨɫɢɬɟɥɶɧɨ Ɂɟɦɥɢ y( x) ;

2) ɭɪɚɜɧɟɧɢɟ

ɬɪɚɟɤɬɨɪɢɢ

ɫɧɚɪɹɞɚ

ɨɬɧɨɫɢɬɟɥɶɧɨ

ɫɚɦɨɥɟɬɚ

y ( x ) ;

3) ɭɪɚɜɧɟɧɢɟ

ɬɪɚɟɤɬɨɪɢɢ

ɫɚɦɨɥɟɬɚ

ɨɬɧɨɫɢɬɟɥɶɧɨ

ɫɧɚɪɹɞɚ

y ( x

) .

Ɉɬɜɟɬ: 1)

2 Xɫɚɦ Xɫɧ 2

, 2) y

2Xɫɧ2

(x )

cc 2

2Xɫɧ2

(x )

, x

0 . Ɉɫɢ X, X' ɢ X'' ɞɟɤɚɪɬɨɜɨɣ ɫɢɫɬɟɦɵ ɤɨɨɪ-

ɞɢɧɚɬ ɧɚɩɪɚɜɥɟɧɵ ɝɨɪɢɡɨɧɬɚɥɶɧɨ ɜɞɨɥɶ ɫɤɨɪɨɫɬɢ ɫɚɦɨɥɟɬɚ, ɚ ɨɫɢ Y, Y' ɢ Y'' – ɜɟɪɬɢɤɚɥɶɧɨ ɜɜɟɪɯ, ɩɪɢ ɷɬɨɦ ɧɚɱɚɥɨ ɤɨɨɪɞɢɧɚɬ ɫɢɫɬɟɦɵ XY ɫɨɜɩɚɞɚɟɬ ɫ ɩɨɥɨɠɟɧɢɟɦ ɫɚɦɨɥɟɬɚ ɜ ɦɨɦɟɧɬ ɜɵɫɬɪɟɥɚ ɩɭɲɤɢ.

Ɂɚɞɚɱɚ 2

Ʌɨɞɤɚ ɩɟɪɟɫɟɤɚɟɬ ɪɟɤɭ ɲɢɪɢɧɨɣ d ɫ ɩɨɫɬɨɹɧɧɨɣ ɨɬɧɨɫɢɬɟɥɶɧɨ ɜɨɞɵ ɫɤɨɪɨɫɬɶɸ ȣ , ɩɟɪɩɟɧɞɢɤɭɥɹɪɧɨɣ ɫɤɨɪɨɫɬɢ ɬɟɱɟɧɢɹ ɪɟɤɢ, ɦɨɞɭɥɶ ɤɨɬɨɪɨɣ ɧɚɪɚɫɬɚɟɬ ɨɬ ɛɟɪɟɝɨɜ ɤ ɫɟɪɟɞɢɧɟ ɪɟɤɢ ɩɨ ɥɢɧɟɣɧɨɦɭ ɡɚɤɨɧɭ, ɦɟɧɹɹɫɶ ɨɬ 0 ɞɨ u. ɇɚɣɬɢ ɬɪɚɟɤɬɨɪɢɸ ɥɨɞɤɢ, ɚ ɬɚɤɠɟ ɫɧɨɫ ɥɨɞɤɢ l ɜɧɢɡ ɩɨ ɬɟɱɟɧɢɸ ɨɬ ɦɟɫɬɚ ɟɟ ɨɬɩɥɵɬɢɹ ɞɨ ɦɟɫɬɚ ɩɪɢɱɚɥɢɜɚɧɢɹ ɧɚ ɩɪɨɬɢɜɨɩɨɥɨɠɧɨɦ ɛɟɪɟɝɭ ɪɟɤɢ.

Ɉɬɜɟɬ:	y	Xd	x , ɩɪɢ y < d/2;	y d	d 2	Xd	x , ɩɪɢ y > d/2;
		u			2	u

l 2X . Ɉɫɶ X ɞɟɤɚɪɬɨɜɨɣ ɫɢɫɬɟɦɵ ɤɨɨɪɞɢɧɚɬ XY ɧɚɩɪɚɜɥɟɧɚ ɜɞɨɥɶ

ɛɟɪɟɝɚ ɪɟɤɢ, ɚ ɨɫɶ Y – ɩɨɩɟɪɟɤ ɪɟɤɢ. ɇɚɱɚɥɨ ɫɢɫɬɟɦɵ ɤɨɨɪɞɢɧɚɬ, ɠɟɫɬɤɨ ɫɜɹɡɚɧɧɨɣ ɫ ɛɟɪɟɝɨɦ ɪɟɤɢ, ɫɨɜɩɚɞɚɟɬ ɫ ɦɟɫɬɨɦ ɨɬɩɥɵɬɢɹ ɥɨɞɤɢ.

Ɂɚɞɚɱɚ 3

ɉɨ ɞɜɢɠɭɳɟɦɭɫɹ ɜɧɢɡ ɷɫɤɚɥɚɬɨɪɭ ɫɩɭɫɤɚɟɬɫɹ ɩɚɫɫɚɠɢɪ ɫɨ ɫɤɨɪɨɫɬɶɸ X ɨɬɧɨɫɢɬɟɥɶɧɨ ɷɫɤɚɥɚɬɨɪɚ. ɋɤɨɪɨɫɬɶ ɷɫɤɚɥɚɬɨɪɚ ɪɚɜɧɚ u. ɋɩɭɫɤɚɹɫɶ ɩɨ ɧɟɩɨɞɜɢɠɧɨɦɭ ɷɫɤɚɥɚɬɨɪɭ ɩɚɫɫɚɠɢɪ ɩɪɨɯɨɞɢɬ N ɫɬɭɩɟɧɟɣ. ɋɤɨɥɶɤɨ ɫɬɭɩɟɧɟɣ N' ɩɪɨɣɞɟɬ ɩɚɫɫɚɠɢɪ, ɫɩɭɫɤɚɹɫɶ ɩɨ ɞɜɢɠɭɳɟɦɭɫɹ ɷɫɤɚɥɚɬɨɪɭ?

<<< < Предыдущая 1 2 34 / 374 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
11.04.2015166.91 Кб61Методичка_Компьютеры.doc
#
16.11.20182.99 Mб37Методичка_КП_IP-тлф-ДО.doc
#
18.11.20192.83 Mб11Методичка_КП_IP-тлф-ДО2012.doc
#
05.05.2019610.3 Кб14Методы логического кодирования (11.01.12).doc
#
05.05.20191.11 Mб36Методы физического кодирования (7.02.2011).doc
#
11.04.20154.96 Mб16Механика.Методика решения задач.pdf
#
11.04.201547.1 Кб11микроэкономика.doc
#
11.04.20151.36 Mб329Млта2008.doc
#
13.07.201945.84 Кб1Многообразие форм собственности.docx
#
11.04.201557.86 Кб43МО ЦОС.контрольная.doc
#
11.04.2015236.54 Кб24МО ЦОС.курсовик.doc