
- •Лекции по курсу
- •4 Видеосигналы 44
- •1 Цифровые фильтры
- •1.1 Сущность явления Гиббса
- •1.2 Весовые функции
- •1.3 Разностное уравнение
- •1.4 Нерекурсивные фильтры
- •1.5 Рекурсивные фильтры
- •1.6 Структурные схемы цифровых фильтров
- •1.7 Импульсная характеристика фильтров
- •1.7.1 Свертка входного сигнала с импульсной характеристикой цифрового фильтра
- •2 Аналого-цифровое преобразование
- •2.1 Цифровая обработка звуковых сигналов
- •2.2 Основные понятия и определения
- •2.3 Структура и алгоритм работы цап
- •2.4 Структура и алгоритм работы ацп
- •2.4.1 Параллельные ацп
- •2.4.2 Ацп с поразрядным уравновешиванием
- •2.4.3 Ацп с плавающей точкой
- •3.1 Методы и стандарты передачи речи по трактам связи, применяемые в современном оборудовании (7 кГц)
- •3.1.1 Импульсно-кодовая модуляция (pcm — Pulse-Code Modulation)
- •3.1.3 Методы эффективного кодирования речи
- •3.1.4 Кодирование речи в стандарте cdma
- •3.1.5 Речевые кодеки для ip-телефонии
- •3.1.6 Оценка качества кодирования речи
- •3.2 Основные понятия цифровой звукозаписи
- •3.2.1 Натуральное цифровое представление данных
- •3.2.2 Кодирование рсм
- •3.3 Формат mp3
- •3.3.1 Сжатие звуковых данных
- •3.3.2 Кратко об истории и характеристиках стандартов mpeg.
- •3.3.3 Каковы отличия режимов cbr, vbr и abr?
- •3.3.4 Какие методы кодирования стерео информации используются в алгоритмах mpeg (и других)?
- •3.3.5 Какие альтернативные mpeg-1 Layer III (mp3) алгоритмы компрессии существуют?
- •3.4 OggVorbis
- •3.6 Flac
- •4 Видеосигналы
- •4.1 Общие положения алгоритмов сжатия изображений
- •4.2 Алгоритмы сжатия
- •4.2.1 Gif (CompuServe Graphics Interchange Format)
- •4.2.3 Jpeg
- •4.2.5 Метод Хаффмана
- •4.2.6 Png (Portable Network Graphics)
- •4.2.7 Tiff (Tagged Image File Format)
- •4.2.8 Pdf (Portable Document Format)
- •4.2.9 Adobe Photoshop Document
- •4.2.10 CorelDraw Document
- •4.2.11 Wmf (Windows Metafile)
- •4.2.12 Bmp (Windows Device Independent Bitmap)
- •4.2.13 Rtf (Microsoft Rich Text Format)
- •4.3 Вейвлет-преобразования
- •4.4 Jpeg2000
- •4.4.1 Общая характеристика стандарта и основные принципы сжатия
- •4.4.2 Информационные потери в jpeg2000 на разных этапах обработки
- •4.5 Видеостандарт mpeg-1
- •4.6 Mpeg-2
- •4.6.1 Стандарт кодирования mpeg-2
- •4.7 Стандарт mpeg-4
- •4.7.1 Особенности стандарта mpeg-4
- •4.7.2 Профайлы в mpeg-4
- •4.8 Стандарт hdtv
- •5 Принципы построения и особенности внедрения систем цифрового тв вещания
- •5.1 Глобальная модель систем цифрового вещания
- •5.2 Определение и классификация систем доставки
- •Приложение п1 Ортогональные разложения функций
- •П2 Дискретизация функций рядами Фурье
- •П4 Частота дискретизации
- •П5 Разрядность
1 Цифровые фильтры
Под фильтрацией будем понимать любое преобразование информации (сигналов, результатов наблюдений), при котором во входной последовательности обрабатываемых данных целенаправленно изменяются определенные соотношения (динамические или частотные) между различными компонентами этих данных.
К основным операциям фильтрации информации относят операции сглаживания, прогнозирования, дифференцирования, интегрирования и разделения сигналов, а также выделение информационных (полезных) сигналов и подавление шумов (помех).
Как известно, преобразование динамики сигналов (и данных, которые несут эти сигналы) осуществляется в системах. Соответственно, фильтры с любым целевым назначением являются частным случаем систем преобразования сигналов, в рамках теории которых они и будут рассматриваться.
.
1.1 Сущность явления Гиббса
Большинство методов анализа и обработки данных представляют собой или имеют в своем составе операцию свертки множества данных s(k) с функцией оператора свертки h(n) (отсчеты импульсной переходной характеристики). Практика цифровой обработки имеет дело только с ограниченными множествами данных (k = 0,1,2,…,K) и коэффициентов оператора (n = 0,1,2,…,N или n = -N,…,1,0,1,…,N для двусторонних операторов). В общем случае, эти ограниченные множества "вырезаются" из бесконечных множеств s(k) и h(n), что равносильно умножению этих множеств на прямоугольную функцию с единичным амплитудным значением, которую называют естественным временным окном или естественной весовой функцией. Учитывая, что произведение функций отображается в спектральной области сверткой их фурье-образов, это может весьма существенно сказаться как на спектральных характеристиках функций, так и на результатах их последующих преобразований и обработки. Основное назначение рассматриваемых в данной теме весовых функций – сведение к минимуму нежелательных эффектов усечения функций.
Чаще всего с изменением частотных характеристик функций приходится сталкиваться при усечении операторов фильтров.
При расчетах фильтров, как правило, задается определенная передаточная характеристика H() фильтра и по ней производится расчет оператора фильтра h(n), количество членов которого может оказаться очень большим даже только по значимым значениям. Усечение может рассматриваться, как результат умножения функции оператора фильтра на селектирующее весовое окно длиной 2N+1. В простейшем случае это окно представляет собой П-образную селектирующую функцию:
hn = h(n)·ПN(n), ПN(n) = 1 при |n| N,
ПN(n) = 0 при |n| > N.
Функция h(n) оператора фильтра, в пределе бесконечная, обуславливает определенную частотную передаточную характеристику фильтра H(). Полному оператору h(n) соответствует исходная частотная характеристика H():
H()
=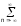 h(n)
exp(-jn).
(1.1)
h(n)
exp(-jn).
(1.1)
Функции во временном окне селекции ПN(n) в частотном пространстве соответствует спектральная функция, которая в определенной степени должна отличаться от функции H(Очевидно, что при усечении оператора h(n), а значит и ряда Фурье (1.1), до конечного числа членов N мы будем иметь усеченный ряд Фурье:
HN()
=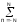 h(n)
exp(-jn),
(1.2)
h(n)
exp(-jn),
(1.2)
при этом сходимость суммы остающихся членов ряда HN() к исходной передаточной функции H() ухудшается и происходит отклонение частотной характеристики фильтра от первоначальной в тем большей степени, чем меньше значение N. Особенно ярко это проявляется на крутых перепадах (разрывах, скачках) в передаточных функциях:
- крутизна перепадов "размывается", т.к. она не может быть больше, чем крутизна (в нулевой точке) последней сохраненной гармоники ряда (1.2);
- по обе стороны "размытых" перепадов появляются выбросы и затухающие осцилляции с частотой, равной частоте последнего сохраненного или первого отброшенного члена ряда (1.2).
Эти эффекты при усечении рядов Фурье получили название явления Гиббса. Рассмотрим явление Гиббса более подробно на примере разложения в ряд Фурье частотной функции единичного скачка G(), которая является Фурье-образом какой-то дискретной временной функции bn. Уравнение функции единичного скачка:
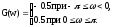 (1.3)
(1.3)
Функция
(1.3) имеет разрыв величиной 1 в точке
=
0 и,
в силу дискретности временной функции
и периодичности ее спектра, в точках
 ,
,
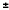 2
и
т.д. Поскольку функция
G()
является
нечетной, ее ряд Фурье не содержит
косинусных членов, и коэффициенты ряда
определяются выражением:
2
и
т.д. Поскольку функция
G()
является
нечетной, ее ряд Фурье не содержит
косинусных членов, и коэффициенты ряда
определяются выражением:
bn
=
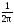
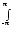 G()
sin(n)
d
=
G()
sin(n)
d
=
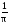
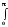 sin(n)
d.
sin(n)
d.
bn = 2/(n·), n- нечетное,
bn = 0, n- четное.

Рисунок 1.1 Значения коэффициентов bn.
Как видно на рис 1.1, ряд коэффициентов bn затухает очень медленно. Соответственно, медленно будет затухать и ряд Фурье функции G():
G() = (2/)[sin + (1/3)·sin 3+ (1/5)·sin 5+....].
G()
=
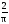
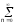 sin[(2n+1)]/(2n+1).
(1.4)
sin[(2n+1)]/(2n+1).
(1.4)
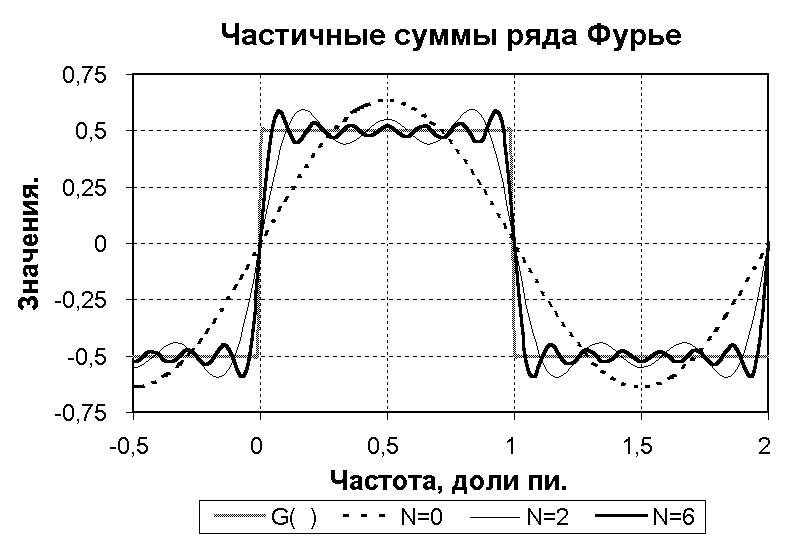
Рисунок 1.2 Явление Гиббса.
Если мы будем ограничивать количество коэффициентов bn, т.е. ограничивать значение N ряда Фурье функции G(), то суммирование в (1.4) будет осуществляться не до ∞, а до значения N. Графики частичных сумм ряда (1.4) в сопоставлении с исходной функцией приведены на рис 1.2. Они наглядно показывают сущность явления Гиббса.
