2 Новые быстрые версии старых алгоритмов

2.1. Сортировки массивов

Справка. Пусть дан массив A = (a₁, a₂, …, a_n), состоящий из n элементов. Для всех элементов определены отношения <, >, =. Тогда сортировка – это процесс, в ходе которого элементы массива переставляются таким образом, что выполняется одно из следующих неравенств:

a₁ ≤ a₂ ≤ … ≤ a_n – массив отсортирован по возрастанию (в прямом порядке) или

a₁ ≥ a₂ ≥ … ≥ a_n – массив отсортирован по убыванию (в обратном порядке).

2.1.1 Метод прямого выбора (SelectSort)

Метод прямого выбора – пример простейшего метода сортировки, обладающего квадратичной трудоёмкостью.

Алгоритм. Просматриваем весь массив, находим минимальный элемент, ставим его на первое место. Потребуется n-1 сравнений и одна перестановка. При втором проходе просматриваем массив, начиная со второго элемента, находим минимум среди просматриваемой (не отсортированной) части и ставим его на второе место, и т.д. Потребуется n – 2 сравнений и одна перестановка. Для полного упорядочивания придется совершить n-1­ проходов не отсортированной части.

Трудоемкость алгоритма:

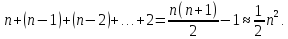
2.1.2 Быстрая сортировка методом двоичных вставок (MergeSort)

Рассмотрим случай, когда количество элементов массива равно степени двойки n =2^k

Алгоритм. 1. Разобьем массив на пары и упорядочим каждую. Получаем серии длины 2.

2. При втором проходе сливаем полученные на первом этапе пары в упорядоченные четвертки. Получаем серии длины 4.

3. При третьем проходе получаем упорядоченные восьмерки, и т.д., пока длина серии не станет равно количеству элементов массива (на k-том проходе).

Оценим трудоемкость алгоритма.

Сначала оценим трудоемкость слияния двух упорядоченных массивов из k и l элементов (считаем только сравнения):

k:

2

3

8

10

14

l:

3

5

6

10

11

Минимальная трудоемкость – меньшее из k и l – min(k,l).

Максимальная трудоемкость: k + l – 1 (единицу вычитаем потому, что сравниваем все элементы, а самый последний просто дописываем к упорядоченной группе).

В MergeSort при получении упорядоченных пар потребуется 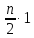действий.

При получении упорядоченных четверок 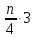действий. Здесь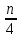есть количество четверок в массиве, а 3 – это максимальная трудоемкость получения упорядоченных четверок (считая только сравнения). Таким образом суммарная трудоемкость сортировки составит:

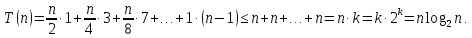
таким образом, трудоемкость MergeSort составляет T(n) = n log₂n .

Теорема. Сортировка на порядок быстрее, чем n log₂n невозможна.

Доказательство. Заметим, что сортировка с помощью некоторого алгоритма эквивалентна блужданию по двоичному дереву, где в узлах этого дерева находятся операторы сравнения. После операции сравнения маршрут двоится. Напомним, что двоичное дерево – граф, у которого ветвление в каждой вершине не больше, чем на две ветви:

Тогда развилками дерева будут сравнения двух элементов массива; а листьями – все возможные варианты перестановки элементов массива (у массива длины n их будет n!).

В этом случае трудоемкость алгоритма – высота дерева, другими словами, максимальный путь от вершины до листа дерева.

Дерево с k листьями имеется высоту не меньше, чем log₂k (т.к. дерево высоты h имеет не более, чем 2^k листьев). Итак, трудоемкость произвольной сортировки будет не меньше, чем log₂(n!).

T(n) ≥ log₂(n!)

Воспользовавшись формулой Стирлинга, имеем:

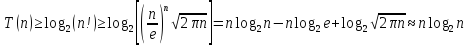
данные величины пренебрежимо малы по сравнению с nlog₂n,

поэтому их во внимание не принимаем

Теорема доказана.