5.4 Иерархия по сложности. Труднорешаемые задачи.
Рассмотрим следующие классы задач:
P (P-time) – класс задач, решаемых за полиномиальное время на ДМТ.
NP (NP-time) – класс задач, решаемых за полиномиальное время на НДМТ.
P-space – класс задач, которые решаются на обычной машине Тьюринга с использованием не более, чем полиномиальной памяти.
NP-space – класс задач, которые могут быть решены на НДМТ с полиномиальной памятью.
Теорема 5.8 P-time P-space
NP-time NP-space
Доказательство. Ясно, что, работая полиномиальное время, мы используем не более, чем полиномиальную память.
Теорема 5.9 P-space=NP-space
Доказательство. Что P-space NP-space очевидно, так как детерминированная машина всегда может рассматриваться как недетерминированная.
Докажем обратное вхождение .
Пусть Т – некоторая задача, которую мы умеем решать на НДМТ М с использованием полиномиальной памяти. Научимся ее решать также с использованием не более, чем полиномиальной памяти на обычной машине Тьюринга М1.
Наша М1 перебирает все возможные варианты в работе исходной НДМТ М и после окончания разбора очередного варианта освобождает память. Поэтому нам потребуется столько же памяти, сколько требуется для работы исходной машины М, но при этом надо вводить дополнительную память для кодирования номера рассматриваемого варианта. Для этого потребуется не более, чем P(n) ячеек(при двоичной кодировке).
Таким образом, теорема доказана, так как работу любой НДМТ с неполиномиальной памятью мы смогли промоделировать на ДМТ с полиномиальной памятью.
Теорема доказана.
Классы сложности.
1? – означает: выполняется ли равенство NP-time = P-time или нет. Ответ на этот вопрос неизвестен и стоит $1000000.
2? – означает: выполняется ли равенство NP-space= Np-time или нет (то есть существуют ли задачи, которым хватает полиномиальной памяти, но за полиномиальное время даже на НДМТ их решить нельзя). Ответ на этот вопрос так же неизвестен.
3?- означает: существуют ли задачи, которые нельзя решить, используя только полиномиальную память. Ответ на этот вопрос дается
Теоремой 5.10
Существует задача( задача непустоты дополнения полурасширенного выражения), которая решаема. Но для ее решения требуется больше чем
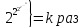
памяти,
где
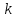- константа, сколь угодно большая. Тем
более эта задача не решаема за
полиномиальное время с использованием
полиномиальной памяти.
Без доказательства.
4? – означает: существуют ли неразрешаемые задачи? Ответ на данный вопрос дается в Разделе 6.
6 Неразрешимые задачи
6.1 Новая модель алгоритма вычислений.
Новая модель алгоритма вычислений представляет собой машину с неограниченными регистрами (МНР).
Определение. МНР – машина с бесконечной лентой ячеек, которые пронумерованы от 1 до ∞, причем в каждой ячейке содержится некоторое натуральное число.
Машина работает по программе, написанной на языке МНР. Язык МНР состоит из команд 4 типов
|
Тип |
Команда |
Действие МНР |
|
Обнуление |
Z(n) |
Xn=0,обнуление n-ой ячейки |
|
Прибавление 1 |
S(n) |
Inc(xn) |
|
Переадресация |
T(m,n) |
xn:=xm |
|
Условный переход |
J(m,n,q) |
If (xn=xm) then goto q?где q – номер строки программы |
В программе на каждой строке находится по одной программе.
Теорема 6.1 Все что можно вычислить, можно вычислить на МНР.
Доказательство. Научимся моделировать на МНР работу машины Тьюринга ( а все что можно вычислить – можно вычислить на машине Тьюринга(тезис Черча)).
Теорема доказана.
Замечание о трудоемкости вычисления на МНР.
С одной стороны на МНР более быстрый доступ к памяти по сравнению с МТ( при работе на МТ мы за один шаг смещаемся только в соседнюю ячейку, а при работе на МНР за один шаг можем переместиться в любую), другой стороны, на МНР значение переменной за одно действие изменяется всего на 1, так что некоторые программы будут быстрее выполнятся на машине Тьюринга, некоторые на МНР.
В данном случае нас интересует не трудоемкость, а только то, разрешима ли данная задача или нет, а классы разрешимых задач у нас совпадают.
Пример. Программа сложения двух чисел:
Вход:
1 2 3 4 5
|
X |
Y |
* |
* |
* |
*… |
Выход:
1 2 3 4
|
* |
* |
X+Y |
* |
*… |
Рисунок 6.1 Иллюстрация работы программы
Программа
1: T(1,3)
2: Z(4)
3: S(3)
4: S(4)
5: J(2,4,7)
6: J(1,1,3) – фактический оператор безусловного перехода
7: -------- - пустой оператор (выход), т. е . любой оператор, ничего не меняющий в третьей ячейке