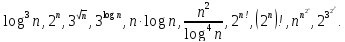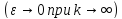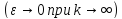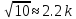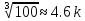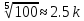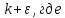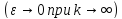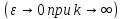1. Основные понятия. Справочный материал

   1. Основные понятия

Центральным понятием курса будет трудоемкость алгоритма. Рассмотрим это понятие подробнее.

Пусть на входе некоторого алгоритма имеется информация объема n (например, n – длина массива, размер матрицы СЛАУ, длина перемножаемых чисел и т.п.), а на выходе ответ – результат обработки входной информации.

Определение. Трудоемкость алгоритма T(n) – максимально возможное количество действия для решения данной задачи среди всех возможных входов длины n.

Замечание. Иногда под сложностью алгоритма подразумевают не максимальное количество операций, а среднюю трудоемкость. Порядок средней и максимальной трудоемкостей, как правило, одинаков.

Характеристики алгоритма:

T(n) – (от англ. Time) – количество операций, необходимых для обработки информации объема n.

S(n) – (от англ. Space) – объём необходимой памяти для обработки информации.

Алгоритмы решения задачи могут быть написаны на разных языках:

• машинные:

  • высокого уровня;

  • низкого уровня;

  • машинные коды;

• математические:

  • математические реализации (машины Тьюринга);

  • конечные автоматы;

  • рекурсивные функции;

Все эти языки эквивалентны с точки зрения набора решаемых задач (любая задача, реализованная на одном языке, может быть переписана на другой), но они неэквивалентны с точки зрения трудоемкости. Трудоемкость алгоритма, реализованного на одном языке, может существенно отличаться от того же алгоритма, записанного на другом языке.

Существуют некоторые договорённости о том, какие именно функции считаются эквивалентными.

Договоренности.

Определение. Функция f(n) и g(n) называются эквивалентными и обозначаются, как f(n) g(n), если выполняется хотя бы одно из двух условий:

либо

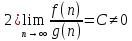
Мы будем пользоваться вторым определением выполнения эквивалентности как наиболее общим.

Пример: эквивалентны по условиям 1) и 2);

по 1) условию не эквивалентны, но эквивалентны по 2) условию.

Определение. Функции f(n) пренебрежимо мала по сравнению с функцией и g(n) обозначается f(n)<<g(n) или f(n) = o(g(n)), если выполняется условие .

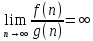2ⁿ >> n² (показательная функция растет быстрее, чем степенная).

n! >> aⁿ >> n^a >> log₂n, где n > 1, a > 0.

Теорема: n! >> aⁿ >> n^a , (a > 0) >> log₂n

Без доказательства.

Договоренность. В дальнейшем под log n будем подразумевать log₂n.

1.2. Справочный материал. Сравнение скорости роста основных функций

Формула Стирлинга:

.

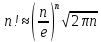Пример. Сравним скорости роста функци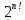й и

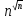
Решение. 1) Прологарифмируем обе функции по основанию 2, получим:

n! и .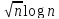

2) Используя формулу Стирлинга: 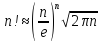, получим:

и

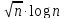
Сократим на :

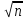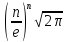и

3) Так как значение некоторых частей выражений много меньше значения других, то их можно не рассматривать:

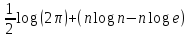и log n.

т.к. nloge << nlogn.

Получаем: nlogn >> logn

n >> 1

Следовательно, 2^n! >>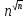

Функция 2^n! растет быстрее, чем

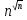
Определение. Будем говорить, что задача решаема за полиномиальное время, если для неё существует некоторый алгоритм с трудоёмкостью T(n) ≤ p(n), где p – некоторый многочлен.

Примерами задач, решаемых за полиномиальное время, являются:

1. сортировки;

2. решение СЛАУ (метод Гаусса).

Чем же хороши задачи, решаемые за полиномиальное время?

Для ответа на этот вопрос рассмотрим две таблицы:

Таблица 1.1. – Время, необходимое для вычисления на машине

с быстродействием 10⁶ опер/сек

n T(n)	10	20	30	50	100
n	10-5 сек	2·10-5 сек	3·10-5 сек	5·10-5 сек	10-4 сек
n logn	3·10-5 сек	8·10-5 сек	15·10-5 сек	3·10-4 сек	7·10-4 сек
n2	10-4 сек	4·10-5 сек	9·10-5 сек	2·5·10-3 сек	10-2 сек
n5	10-1 сек	3·2 сек	10-5 сек	5.2 мин	≈ 3 часа
2n	10-3 сек	1 сек	18 мин	36 лет	3·1016 лет

Таблица 1.2. – Объем доступной решаемой задачи за одно

и то же время (таблица прогресса)

машины T(n)	Современные	В 10 раз быстрее современных	30
n	k	10k	100k
n logn	k
n2	k		10k
n3	k
n5	k
Неполиномиальные алгоритмы
2n	k	3.3 + k	6.6 + k
n!	k

Комментарии к таблице прогресса. При повышении производительности машины в несколько раз для алгоритма с полиномиальной производительностью объем доступной решаемой задачи повышается в разы, а у неполиномиальных алгоритмов увеличивается «на сколько-то», то есть НЕ в разы.

Домашнее задание №1

Отсортировать по скорости роста, начиная с наименьшей: