2. Комбинаторика

Комбинаторика – раздел математики, посвященный решению задач выбора и разложения элементов некоторого множества в соответствии с заданными правилами. Каждое правило определяет способ построения некоторой конструкции из элементов исходного множества. Простейшими примерами комбинаторных конструкций являются перестановки, размещения и сочетания, рассматриваемые ниже.

1. Перестановки, размещения и сочетания без повторений

Пусть дано множество M={a₁, a₂, a₃, ..., a_n}. Набор элементов из множестваМ называется выборкой объема m из n элементов. Выборка называется упорядоченной, если в ней задан порядок следования. Если порядок следования не является существенным, то выборка называется неупорядоченной.

Размещениями без повторений из n элементов по m называются упорядоченные выборки без повторений элементов множества, которые отличаются одна от другой либо составом элементов, либо порядком их расположения. Число размещений из n элементов по m будем обозначать .

Пример 2.1. Сколько различных трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5 при условии, что ни одна цифра не повторяется?

Составить разные числа можно способами.

Перестановками без повторений из n элементов называются размещения из n элементов по n. Обозначим число перестановок объема n как P_n.

Пример 2.2.Сколькими способами можно расставить на полке 6 томов книг?

Это можно осуществить способами.

Сочетаниями без повторений из n элементов по m называются любые подмножества из m элементов исходного множества. Число сочетаний без повторений будем обозначать .

Пример 2.3. На тренировках занимаются 8 баскетболистов. Сколько разных стартовых пятерок может быть образовано тренером?

Т.к. при образовании пятерки важен только ее состав, то достаточно определить пятерок.

Число обладает следующими свойствами:

1. ;

2. ;

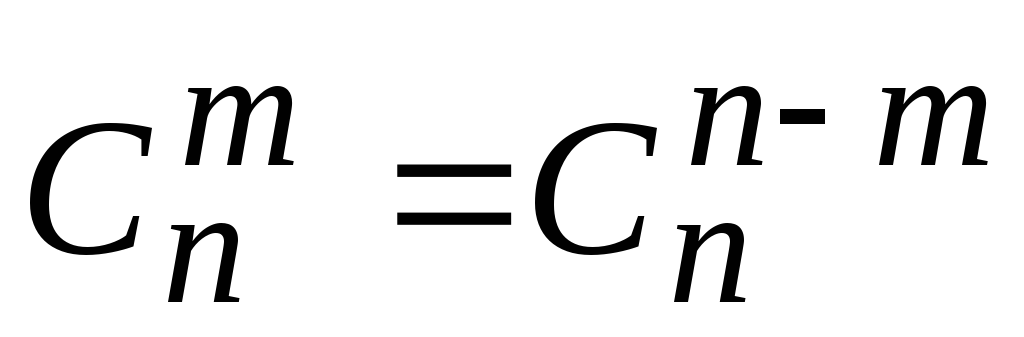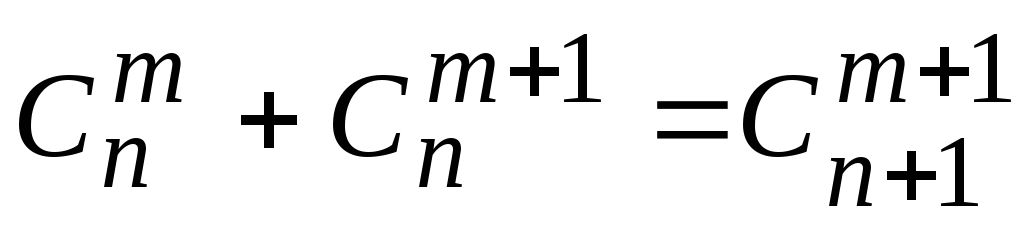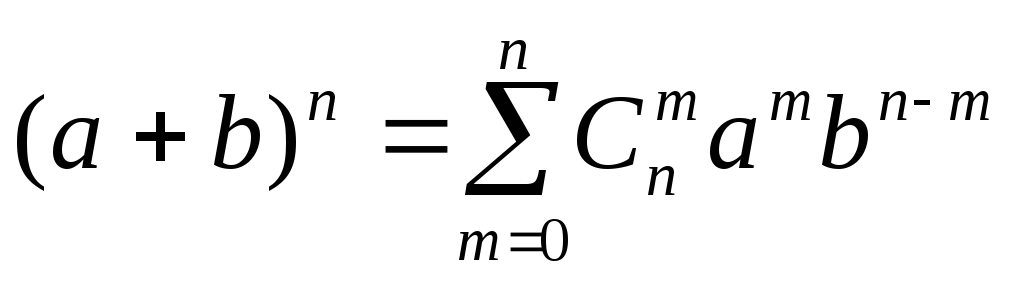3. при любых a, b  R (бином Ньютона).

В силу свойства 3, числа называют биномиальными коэффициентами.

2. Выборки с повторениями

Размещениями с повторениями из n элементов по m называются упорядоченные выборки из m элементов множества, в которых элементы множества могут повторяться. Количество всех размещений с повторениями обозначим .

Пример 2.4. Сколько всего трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5?

.

Сочетаниями с повторениями из n элементов по m называются неупорядоченные выборки из m элементов множества, в которых элементы множества могут повторяться. Число всех сочетаний с повторениями обозначим .

Пример 2.5. Сколько различных вариантов количества очков может выпасть при бросании двух кубиков?

.

Перестановками с повторениями из n элементов по k называется упорядоченная выборка из k элементов множества, в которой каждый элемент множества встречается k_i раз (причем, k₁+k₂+...+k_n=k). Число перестановок с повторениями обозначается

Пример 2.6.Сколько разных слов можно образовать при перестановке букв слова «математика»?

В слове «математика» буква «м» встречается 2 раза, «а» – 3 раза, «т» – 2 раза, «е» – 1 раз, «и» – 1 раз, «к» – 1 раз. Поэтому число различных слов равно

При подсчете числа комбинаций используют два правила: правило суммы и правило произведения.

Правило суммы. Если объект А можно выбрать m способами, а объект B – k способами, то объект «либо А, либо В» можно выбрать m+k способами.

Правило произведения. Если объект А можно выбрать m способами, а после каждого такого выбора объект В можно выбрать k способами, то пару объектов А и В можно выбрать mk способами.

Пример 2.7. Сколько разных четырехзначных чисел можно составить из цифр 0, 1, 2?

Из цифр 0, 1, 2 можно составить число, но сюда входят числа, у которых первая цифра нуль, которые не являются четырехзначными. Таких чисел будет. Поэтому ответ 81 – 27 = 54.

Пример 2.8 Сколько различных пятизначных чисел можно составить из цифр числа 1111222345600?

Разделим все составленные числа на группы по первой цифре в числе. Таких групп будет три.

1-я группа. У чисел из этой группы на первом месте стоит «единица». Эти числа имеют вид 1****, где на место **** выбираются 4 цифры из набора 111222345600. Перечислим все возможные случаи. Это могут быть либо 3 «единицы» и любая цифра из множества {2,3,4,5,6,0}, либо 2 «единицы» и 2 «двойки», либо 2 «единицы» и 2 «нуля», либо 2 «единицы» и 2 любые цифры из множества {2,3,4,5,6,0}, либо 3 «двойки» и любая цифра из множества {1,3,4,5,6,0}, либо 2 «двойки» и 2 «нуля», либо 2 «двойки» и 2 любые цифры из множества {1,3,4,5,6,0}, либо 2 «нуля» и 2 любые цифры из множества {1,2,3,4,5,6}, либо 4 любые цифры из множества {1,2,3,4,5,6,0}. Всего таких чисел будет:

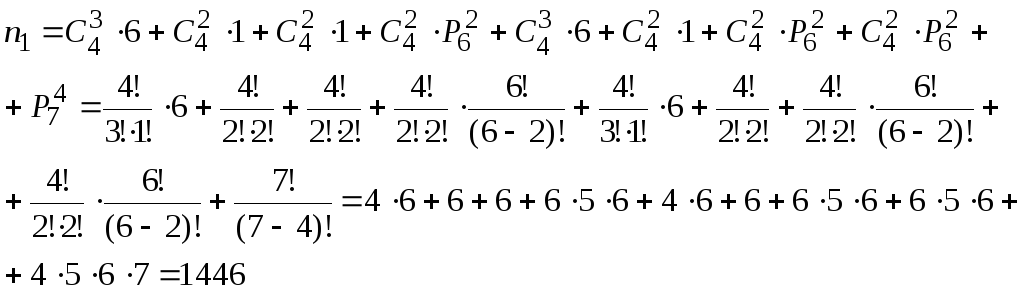2-я группа. У чисел из этой группы на первом месте стоит «двойка». Эти числа имеют вид 2****, где на место **** выбираются 4 цифры из набора 111122345600. Перечислим все возможные случаи. Это могут быть либо 4 «единицы», либо 3 «единицы» и любая цифра из множества {2,3,4,5,6,0}, либо 2 «единицы» и 2 «нуля», либо 2 «единицы» и 2 «двойки», либо 2 «единицы» и 2 любые цифры из множества {2,3,4,5,6,0}, либо 2 «двойки» и 2 «нуля», либо 2 «двойки» и 2 любые цифры из множества {1,3,4,5,6,0}, либо 2 «нуля» и 2 любые цифры из множества {1,2,3,4,5,6}, либо 4 любые цифры из множества {1,2,3,4,5,6,0}. Всего таких чисел будет:

3-я группа. У чисел из этой группы на первом месте стоит ни «единица», ни «двойка», ни «нуль», т.е. одна из цифр множества {3,4,5,6}. Первую цифру можно выбрать 4 способами. Оставшиеся 4 цифры выбираются из набора 1111222345600 с учетом того, что одна из цифр множества {3,4,5,6} уже выбрана. Перечислим все возможные случаи. Это могут быть либо 4 «единицы», либо 3 «единицы» и любая цифра из множества {2,3,4,5,6,0}, либо 2 «единицы» и 2 «двойки», либо 2 «единицы» и 2 «нуля», либо 2 «единицы» и 2 любые цифры из множества {2,3,4,5,6,0}, либо 3 «двойки» и любая цифра из множества {1,3,4,5,6,0}, либо 2 «двойки» и 2 «нуля», либо 2 «двойки» и 2 любые цифры из множества {1,3,4,5,6,0}, либо 2 «нуля» и 2 любые цифры из множества {1,2,3,4,5,6}, либо 4 любые цифры из множества {1,2,3,4,5,6,0}. Всего таких чисел будет:

Всего пятизначных чисел будет:

N=n₁+n₂+n₃=1446+1423+3116=5985.

3. Формулы включений и исключений

Мощностью конечного множества называется количество элементов в нем. Если множество А имеет n элементов, то пишут

Пусть имеется два пересекающихся множества А и В. Изобразим их на диаграмме Венна. Тогда имеет место следующая формула:

Для трех пересекающихся множеств выполняется:

Пример 2.9. В месяце было 12 дождливых, 8 ветреных, 4 холодных дня, дождливых и ветреных – 5, дождливых и холодных – 3 , ветреных и холодных – 2, дождливых, ветреных и холодных – 1 день. Сколько дней была плохая погода?

Пусть А – дождливые дни, В – ветреные дни, С – холодные, D – дни с плохой погодой. Тогда . Количество дней с плохой погодой:

В общем случае формула включений и исключений для k множеств имеет вид:

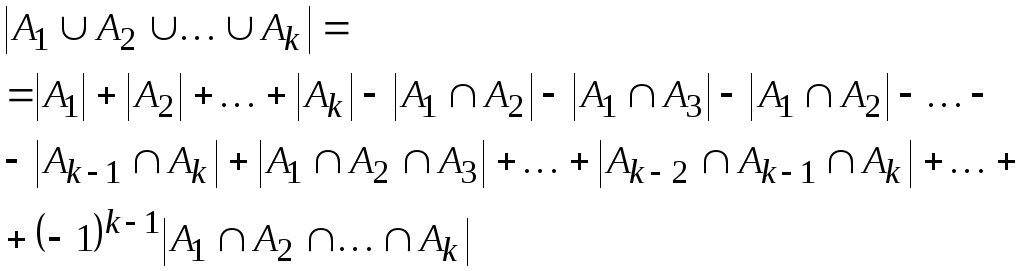
Пусть множество А состоит из N элементов и имеется n одноместных отношений (свойств) . Каждый элемент множества может обладать или не обладать любым из этих свойств. Обозначим черезчисло элементов, обладающих свойствамии, может быть, некоторыми другими. Тогда числоN(0) элементов, не обладающих ни одним из свойств , вычисляется по следующей формуле:

, где

Обобщая, получаем формулу, позволяющую вычислить число N(r) элементов, обладающих ровно r свойствами .

(1)

Определим функцию [x] для вещественных чисел как наибольшее целое число, не превосходящее x. Число [x] называется целой частью числа x. Для положительных чисел а и b значение функции равно количеству чисел из множества{1, 2,…, b}, которые делятся на а, т.е. кратны а.

Пример 2.10.Сколько положительных трехзначных чисел делятся ровно на одно из чисел 3, 5 или 7?

Обозначим P₃ – свойство делимости на 3, P₅ – на 5, P₇ – на 7. Тогда

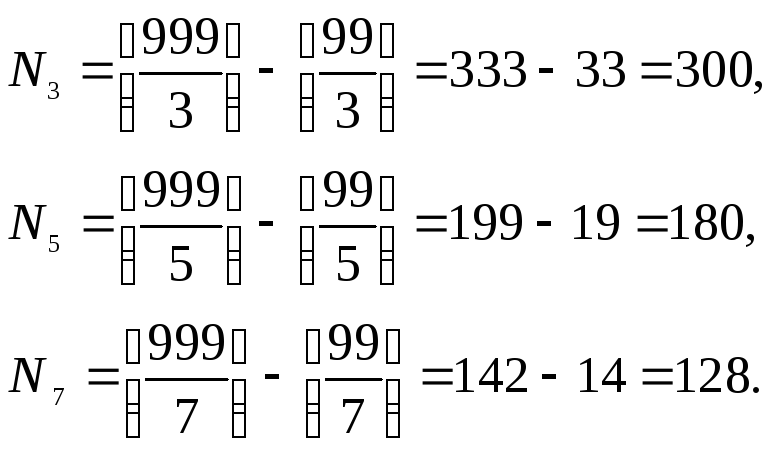
Так как N_3,5 – число чисел, делящихся одновременно на 3 и 5, а наименьшее общее кратное 3 и 5 равно 15, то . Аналогично,

По формуле (1) находим искомое число чисел:

4. Рекуррентные соотношения. Возвратные последовательности

Рекуррентным соотношением называется соотношение вида , которое позволяет вычислить все члены последовательности, если заданы ее первыеk членов.

Пример 2.11. Формула задает арифметическую прогрессию.

Последовательность называетсявозвратной, если для всех n и некоторого k выполняется гдеp_i = const.

Пример 2.12. Геометрическая прогрессия – это возвратная последовательность, так как . Следовательно, выполняется

Многочлен называетсяхарактеристическим для возвратной последовательности.

Множество всех последовательностей, удовлетворяющих данному рекуррентному соотношению, называется общим решением.

Описание общего решения имеет аналоги с описанием решения обыкновенного дифференциального уравнения с постоянными коэффициентами. Пусть  – корень характеристического уравнения. Тогда общее решение рекуррентного соотношения можно найти следующим образом:

1. если _i – корень кратности 1 (i=1,…,k), то общее решение имеет вид 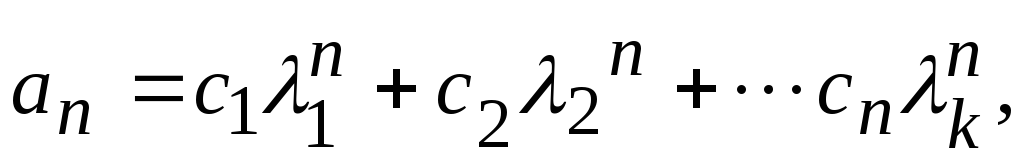гдеc_i = const (i=1,…,k).

2. если _i – корень кратности r_i (i=1,…,k), то общее решение имеет вид 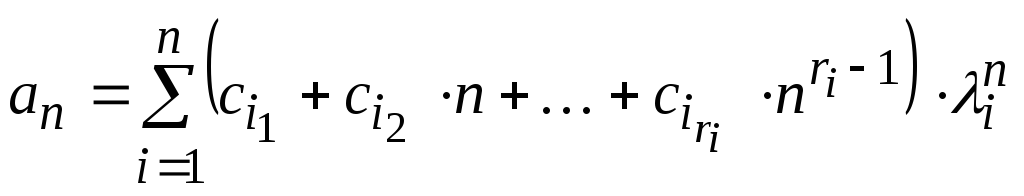, где – произвольные константы (i=1,…,n, j=1,…,r_i).

Зная общее решение рекуррентного соотношения, по начальным условиям можно найти неопределенные постоянные и тем самым получить частное решение рекуррентного уравнения с данными начальными условиями.

Пример 2.13. Найти последовательность {a_n}, удовлетворяющую рекуррентному соотношению

Составим характеристический многочлен

Для нахождения корней сгруппируем слагаемые .

Составим характеристическое уравнение Его корнями являются числа. Следовательно, общее решение рекуррентного соотношения имеет вид:. Используя начальные условия, получим систему:

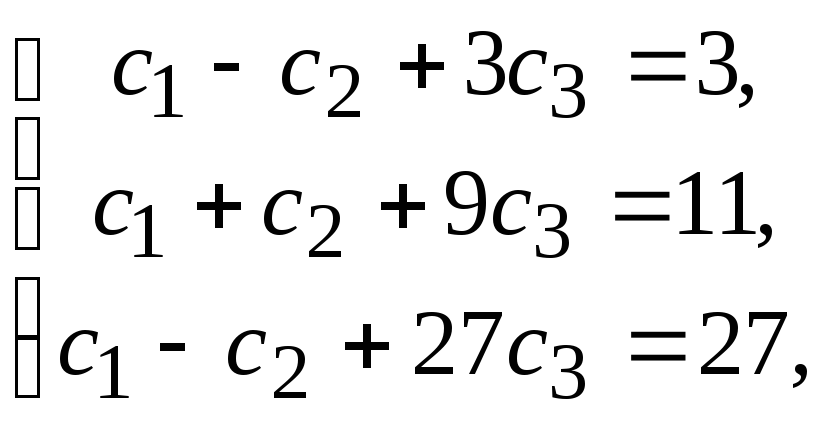
решая которую находим с₁=1, с₂= 1, с₃=1. Таким образом, .