3. Алгебра логики

   1. Булевы функции

Функцией алгебры логики или булевой функцией называется функция n переменных если аргументы функции являются булевыми переменными (т.е. ), и функция может принимать только два значения: 0 или 1. Таким образом, булева функцияБулевы функции называются такжепереключательными функциями. Каждая комбинация значений аргументов булевой функции называется набором. Для функции n переменных количество разных наборов равно 2ⁿ.

Булева функция задается таблицей истинности:

x1	x2	x3	…	xn-1	xn	f(x1, x2,…,xn)
0	0	0	…	0	0	f (0,0,…,0,0)
0	0	0	…	0	1	f (0,0,…,0,1)
…	…	…	…	…	…	…
1	1	1	…	1	0	f (1,1,…,1,0)
1	1	1	…	1	1	f (1,1,…,1,1)

Рассмотрим булевы функции одного аргумента. Эти функции определены на двух наборах. Приведем обозначения и названия этих функций.

x	0	1	f1	f2
0	0	1	0	1
1	0	1	1	0

Функции 0 и 1 называются соответственно тождественным нулем и тождественной единицей. Функция f₁ называется тождественной функцией и обозначается через x. Функция f₂ называется отрицанием x и обозначается .

Рассмотрим часто используемые булевы функции двух аргументов. Эти функции определены на четырех наборах.

x1	x2	f3	f4	f5	f6	f7	f8
0	0	0	0	0	1	1	1
0	1	0	1	1	1	0	1
1	0	0	1	1	0	0	1
1	1	1	1	0	1	1	0

Приведем обозначения и названия этих функций. Функция f₃ называется конъюнкцией x₁ и x₂ и обозначается x₁x₂. Функция f₄ называется дизъюнкцией x₁ и x₂ и обозначается . Функцияf₅ называется суммой по модулю 2 и обозначается . Функцияf₆ называется импликацией и обозначается (читается x₁ влечет x₂). Функция f₇ называется эквивалентностью и обозначается x₁  x₂ (читается x₁ эквивалентно x₂). Функция f₈ называется штрихом Шеффера и обозначается x₁|x₂ (читается не x₁ и x₂).

С помощью операции суперпозиции из этих элементарных функций можно построить функции большего числа аргументов. Заметим, что булеву функцию можно однозначно определить перечислением всех наборов, на которых она принимает значение 1.

Функция существенно зависит от переменнойx_i, если для любых значений. В противном случае переменнаяx_i - фиктивная. Наборы, отличающиеся значением только одной переменной x_i, называются соседними.

2. Булева алгебра

Множество булевых функций с операциями  (дизъюнкция), (конъюнкция), (отрицание) называетсябулевой алгеброй. Операция отрицание имеет самый высокий приоритет, затем идет конъюнкция, а затем дизъюнкция. Рассмотрим основные аксиомы булевой алгебры (в аксиомах x, y, z могут быть булевыми переменными или функциями).

1. 

коммутативность

2. 

ассоциативность

3. 

идемпотентность

4. 

свойства констант

5. 

0=1

аксиомы отрицания

6. 

дистрибутивность

7. закон исключения третьего

8. закон противоречия

9. 

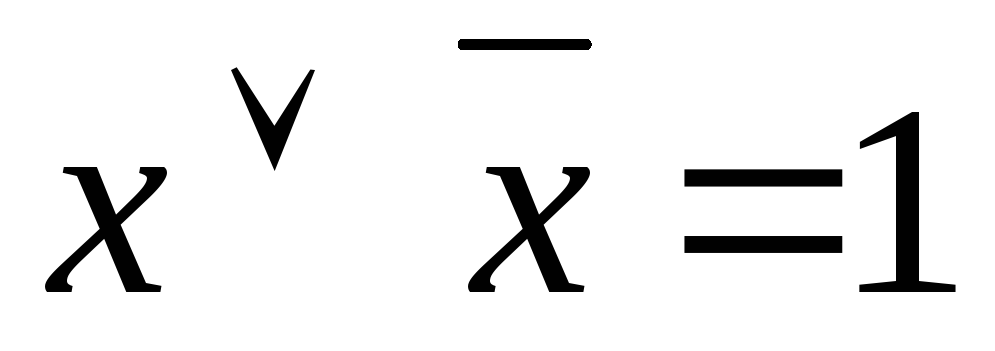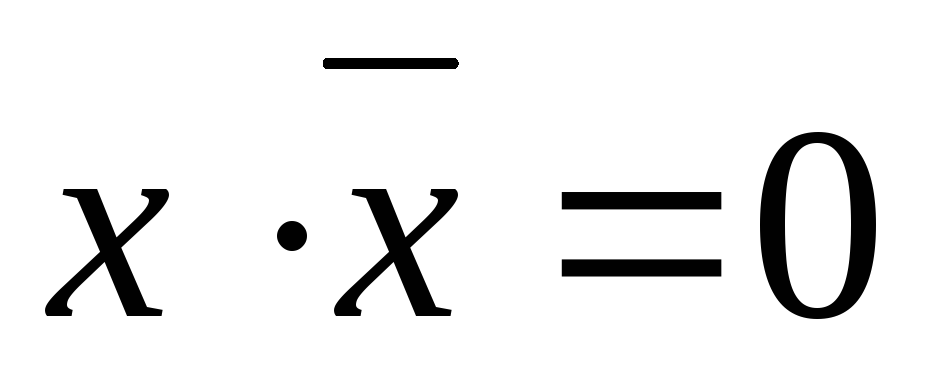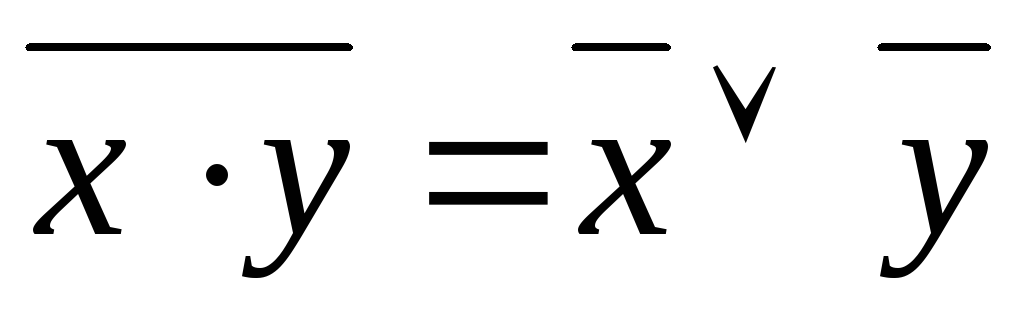
законы де Моргана

Если в формуле несколько одинаковых по старшинству операций следуют друг за другом, то они выполняются слева направо.

Рассмотрим несколько дополнительных законов булевой алгебры, которые могут быть доказаны с помощью перечисленных выше аксиом и которые часто используются для эквивалентных преобразований.

1. поглощение

2. склеивание

3. Нормальные формы

Булевы функции удобнее задавать в виде формул. Одной функции может соответствовать множество формул, содержащих аргументы функции, знаки дизъюнкции, конъюнкции и отрицания.

Элементарной дизъюнкцией называется дизъюнкция конечного множества переменных или их отрицаний, в котором каждая переменная встречается не более одного раза.

Пример 3.1. ,x₁

Элементарной конъюнкцией называется конъюнкция конечного множества переменных или их отрицаний, в котором каждая переменная встречается не более одного раза.

Пример 3.2. ,

Дизъюнктивной нормальной формой (днф) называется дизъюнкция конечного множества попарно различных элементарных конъюнкций.

Пример 3.3. ,

Аналогично, можно определить конъюнктивную нормальную форму (кнф), как конъюнкцию конечного множества попарно различных элементарных дизъюнкций.

Пример 3.4. ,

В примере видно, что является одновременно днф и кнф.

Для любой функции можно найти ее представление в днф и кнф, используя аксиомы алгебры логики.

Пример 3.5. Найти днф, кнф для функции

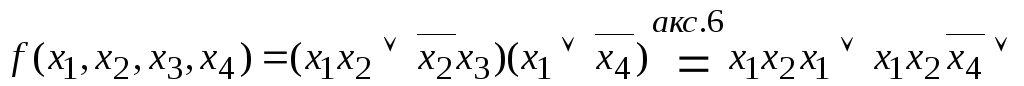
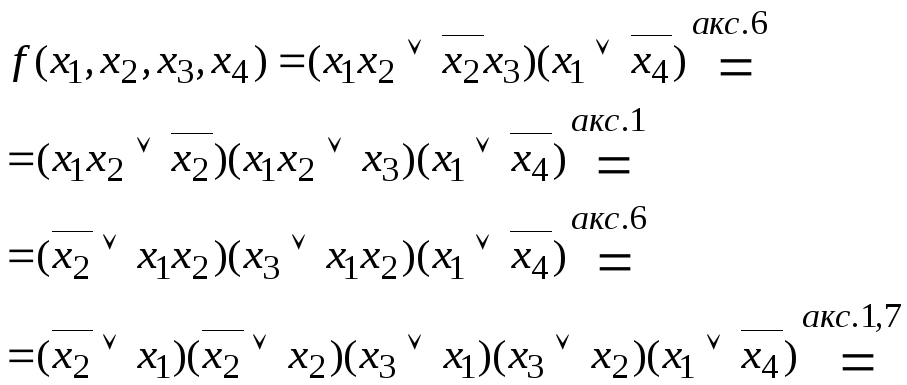
–Днф.

–кнф.

Любая булева функция может иметь много представлений в виде днф и кнф. Особое место среди этих представлений занимают совершенные днф (сднф) и совершенные кнф (скнф).

Конституентой единицы k¹ набора называется конъюнкция всех переменных, образующих этот набор. Причем, переменная входит в конъюнкцию с отрицанием, если она на данном наборе равна 0 и без отрицания, если она равна 1. Конституентой нуля k⁰ данного набора называется дизъюнкция всех переменных, образующих этот набор. Переменная входит в дизъюнкцию без отрицания, если она на этом наборе равна 0 и с отрицанием, если она равна 1. Совершенная дизъюнктивная нормальная форма функции f – дизъюнкция k¹ тех наборов, на которых функция принимает значение 1. Совершенная конъюнктивная нормальная форма функции f – конъюнкция k⁰ тех наборов, на которых функция принимает значение 0. Представление функции в СДНФ или СКНФ единственно. Совершенные формы легко строить по таблице истинности.

Пример 3.6. Построим СДНФ и СКНФ для функции f, для которой задана таблица истинности.

x1	x2	x3	f
0	0	0	1
0	0	1	0
0	1	0	0
0	1	1	1
1	0	0	1
1	0	1	0
1	1	0	0
1	1	1	1

Для построения СДНФ рассмотрим все наборы, на которых функция принимает значение 1, и выпишем для этих наборов все k¹:

, ,,.

Тогда СДНФ имеет вид:

Для построения СКНФ рассмотрим все наборы, на которых функция принимает значения 0, и выпишем для этих наборов k⁰:

, ,,.

Тогда СКНФ имеет вид:

Для построения СДНФ из ДНФ можно домножить элементарную конъюнкцию на (если переменная x_i отсутствует в элементарной конъюнкции) и применить закон дистрибутивности.

Пример 3.7. Найти СДНФ для функции

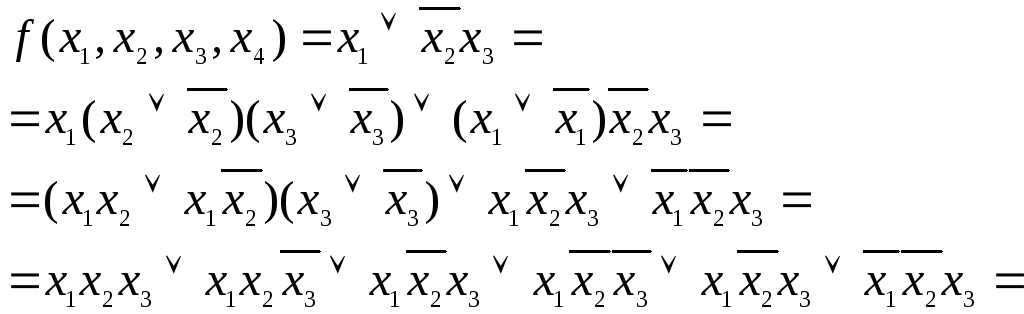
–СДНФ.

Для построения СКНФ из КНФ в элементарную дизъюнкцию, не содержащую переменную x_i, добавляем и применяем закон дистрибутивности.

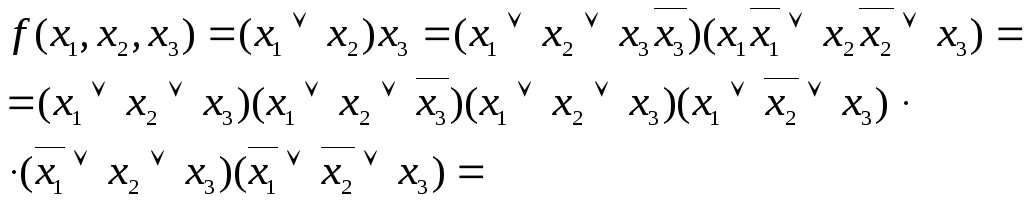
Пример 3.8. Найти СКНФ для функции – СКНФ.

В дальнейшем для представления СДНФ функции f будем указывать номера k¹, на которых функция равна 1. Для определения набора необходимо перевести номер k¹ в двоичное число.

Пример 3.9. Пусть СДНФ функция f определяется следующим образом.

=

Переведем номера k¹ в двоичные числа

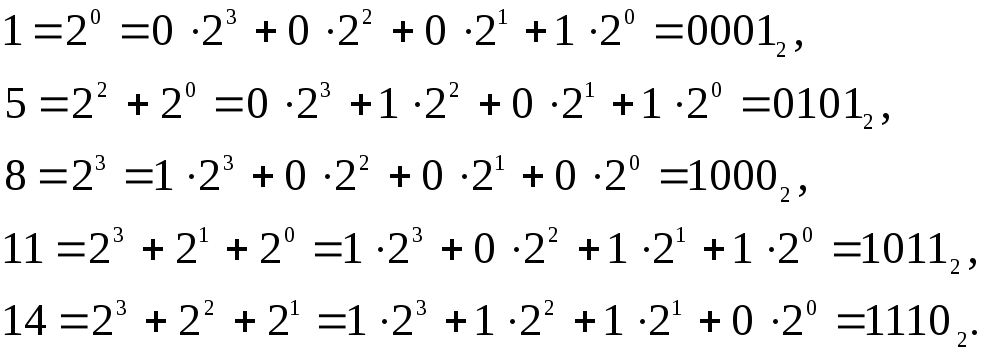
Таким образом, f обращается в 1 на наборах

(0,0,0,1), (0,1,0,1), (1,0,0,0), (1,0,1,1), (1,1,1,0).

Аналогично, для представления функции в СКНФ будем использовать запись с указанием номеров k⁰, на которых функция равна 0.

Пример 3.10. =.

Переведем номера k⁰ в двоичные числа

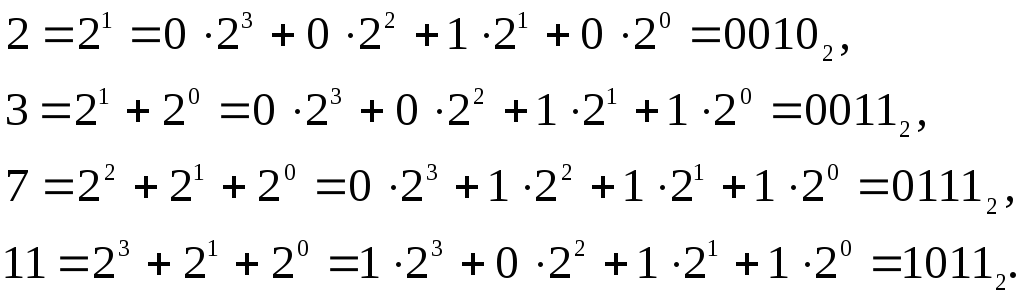
Функция f обращается в 0 на наборах

(0,0,1,0), (0,0,1,1), (0,1,1,1), (1,0,1,1).

4. Минимизация булевых функций в классе ДНФ

Будем получать выражение для булевой функции в виде ДНФ с минимальным числом вхождений переменных. Будем предполагать, что функция представлена в СДНФ.

Элементарная конъюнкция называется импликантой , если она равна 0 на тех наборах, на которыхf обращается в 0. Простой импликантой называется импликанта, в которой отбрасывание любой буквы ведет к получению элементарной конъюнкции, которая не является импликантой.

Пример 3.11. Найдем импликанты и простые импликанты для функции . Всего имеется 8 элементарных конъюнкций с переменнымиx₁, x₂. Приведем их таблицы истинности.

x1	x2	x1x2				x1x2			x1	x2
0	0	1	1	0	0	0	1	1	0	0
0	1	1	0	1	0	0	1	0	0	1
1	0	0	0	0	1	0	0	1	1	0
1	1	1	0	0	0	1	0	0	1	1

Из таблиц истинности заключаем, что ,, x₁x₂, , x₂ являются импликантами функции f. Из них простыми являются иx₂.

Дизъюнкция всех простых импликант называется сокращенной ДНФ. Сокращенная ДНФ может содержать лишние импликанты, удаление которых не меняет таблицу истинности. При удалении из сокращенной ДНФ всех лишних импликант получаем тупиковую ДНФ. Выбор из всех тупиковых ДНФ формулы с наименьшим числом вхождений переменных дает минимальную ДНФ.

Известны аналитические и графические способы построения минимальной ДНФ.

5. Метод Квайна получения минимальной ДНФ

Процесс нахождения минимальной ДНФ из СДНФ можно разбить на следующие этапы: нахождение сокращенной ДНФ, нахождение всех тупиковых ДНФ, выбор из всех тупиковых минимальной ДНФ.

Этап 1. Нахождение сокращенной ДНФ.

Будем предполагать, что функция задана в СДНФ. Метод Квайна основан на том, что если выполнить в СДНФ все возможные неполные склеивания по формуле , а затем все поглощения по формуле, гдеА – элементарная конъюнкция, то получим сокращенную ДНФ. Для удобства выполнения операции склеивания представим все k¹ для наборов из СДНФ в виде их двоичных номеров и разобьем номера на группы по количеству единиц. Склеивание возможно между элементами соседних групп. Элементы, участвующие в склеивании будем помечать *. Результат склеивания – набор импликант и, возможно, простые импликанты, не отмеченные символом *. Для наборов, соответствующих импликантам, на месте отсутствующей переменной будем писать знак X.

Пример 3.12. Результат склеивания наборов 0110 и 1110 – набор Х110, который соответствует импликанте .

Далее разобьем полученное множество импликант на группы по расположению Xи произведем все возможные склеивания внутри каждой группы. Получим новое множество импликант для дальнейшего склеивания и, возможно, простые импликанты, не участвовавшие в склеивании. Склеивание продолжаем до тех пор пока, это возможно. Результат этого этaпа – построение всех простых импликант, т.е. сокращенной ДНФ.

Этап 2.Нахождение минимальной ДНФ.

По найденным на предыдущем этапе простым импликантам составляем импликантную таблицу, заголовки строк которой – простые импликанты, заголовки столбцов – K¹ наборов из СДНФ. В таблице помечаем пересечение строки и столбца, если заголовок строки является импликантой заголовка столбца. Если в столбце имеется только одна метка, то импликанта, соответствующая этой строке, называется существенной, и она обязательно должна присутствовать в минимальной ДНФ. Включив эту импликанту в минимальную ДНФ, можно исключить из дальнейшего рассмотрения строку и все столбцы с пометками для этой импликанты.

Если все пометки i-ой строки имеются также в j-ой строке, то j-я строка доминирует над i-ой, и i-ую строку можно исключить из дальнейшего рассмотрения. В частности, из рассмотрения исключаются строки без пометок.

Если все пометки k-го столбца имеются также в m-ом столбце таблицы, то m-ый столбец доминирует над k-ым и m-ый столбец можно исключить из дальнейшего рассмотрения. Исключение существенных импликант, доминируемых строк и доминирующих столбцов проводят до тех пор, пока это возможно. Полученная после таких преобразований таблица называется циклической.

Для выбора минимальной ДНФ в циклической таблице используют процедуру ветвления. Согласно алгоритму этой процедуры выбирают столбец с минимальным количеством пометок (таких столбцов может быть несколько) и для этих столбцов выбирают из строк, содержащих пометку в выбранном столбце, ту, которая содержит максимальное количество пометок и включают ее в минимальную ДНФ. После этого исключают строку, соответствующую найденной импликанте, и все помеченные в этой строке столбцы из дальнейшего рассмотрения. Если появилась строка, в которой во всех столбцах стоят пометки, то эту импликанту включают в минимальную ДНФ и на этом процесс нахождения минимальной ДНФ закончен. В противном случае выполняют преобразования для получения новой циклической таблицы.

В результате описанных преобразований таблицы должны получить минимальную ДНФ.

Пример 3.13. Найдем минимальную ДНФ для функции

=.

Выпишем все наборы, на которых функция принимает значение 1.

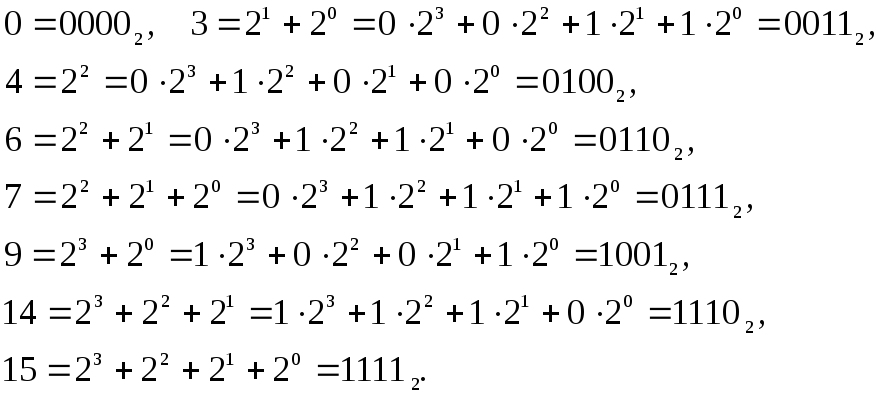
Разобьем наборы на группы по количеству единиц. Первая группа состоит из наборов, не содержащих единиц: {0000}. Вторая группа состоит из наборов, содержащих одну единицу: {0100}. Третья группа состоит из наборов, содержащих две единиц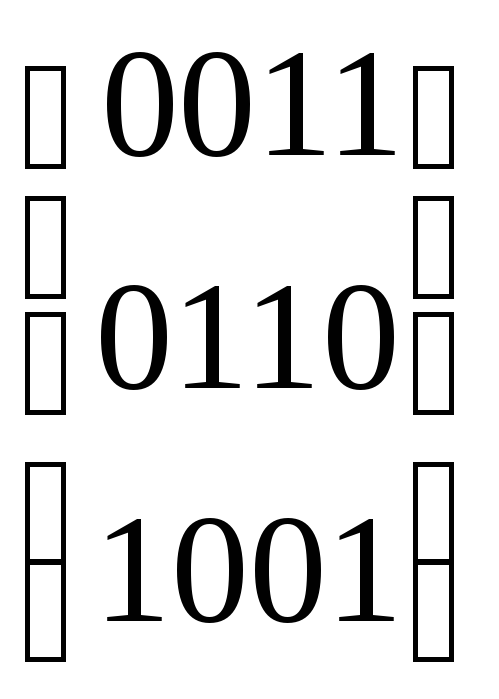ы: . Четвертая группа состоит из наборов, содержащих три единицы: . Пятая группа состоит из наборов, содержащих четыре единицы:{1111}.

Выполним все возможные склеивания между элементами соседних групп, помечая наборы, участвующие в склеивании.

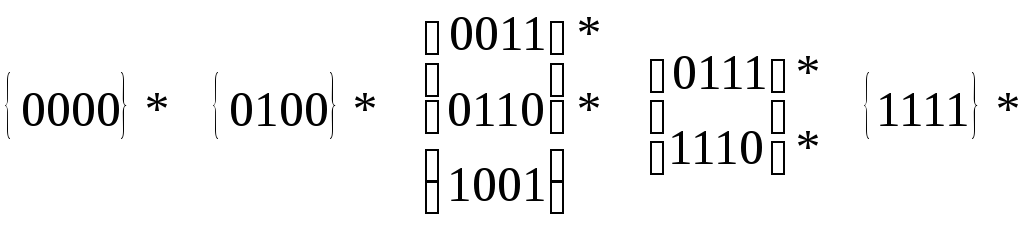
Результаты склеивания – импликанты, являющиеся K¹ для наборов

0Х00, 01Х0, 0Х11, 011Х, Х110, Х111, 111Х.

Импликанта, являющаяся K¹ для набора 1001 – простая.

Разобьем все полученные в результате склеивания импликанты по положению Х на группы.

1-я группа:

2-я группа:

3-я группа:

4-я группа:

Произведем все возможные склеивания внутри каждой группы, помечая наборы, участвующие в склеивании.

Результат склеивания – импликанта, соответствующая X11X, и набор простых импликант, соответствующих 0Х00, 0Х11, 01Х0. Дальнейшее склеивание осуществить нельзя, поэтому Х11Х соответствует простой импликанте. Можно переходить к составлению импликантной таблицы.

	0000	0011	0100	0110	0111	1001	1110	1111
1001						v
0Х00	v		v
01Х0			v	v
0Х11		v			v
Х11Х				v	v		v	v

Импликанты, соответствующие 0Х00, 0Х11, 1001, X11X – существенные, поэтому они обязательно входят в минимальную ДНФ. Удалим строки и столбцы для этих импликант из таблицы. Вычеркнутся все столбцы, следовательно, на этом процесс поиска минимальной ДНФ закончен.

Минимальная ДНФ имеет следующий вид:

6. Нахождение минимальной ДНФ с помощью карт Карно

Этот метод используется для формул с малым числом переменных. Карта Карно для функции n переменных содержит 2ⁿ ячеек, каждая из которых соответствует одной из 2ⁿ возможных комбинаций значений n булевых переменных x₁, x₂, …, x_n. Две соседние ячейки отличаются значением только одной переменной. В случае функции трех переменных карту Карно можно представить в следующем виде:

В

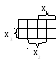се ячейки, отмеченные скобкойx_i (по строке и столбцу), представляют наборы с x_i =1, а в неотмеченных строках и столбцах ячейки соответствуют наборам с x_i =0.

Вслучае четырех переменных карта Карно имеет следующий вид:

Булева функция может быть представлена на карте Карно выделением на карте ячеек, соответствующих наборам, на которых функция принимает значение 1. В этих ячейках будем писать 1. Незаполненные ячейки соответствуют нулям функции.

Пример 3.14. Заполним карту Карно для функции

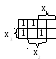
2^k соседних ячеек, содержащие единицы, называются покрытием в том случае, если они расположены в виде прямоугольника или квадрата. При этом считается, что ячейки на противоположных концах строки или столбца являются соседними, как будто карта расположена на торе. Каждое покрытие соответствует импликанте. Покрытие, состоящее из двух ячеек, соответствует произведению всех переменных кроме одной, значением которой отличаются эти ячейки. Покрытие из четырех ячеек соответствует произведению, в котором отсутствуют две переменные и т.д. Чем больше ячеек в покрытии, тем проще импликанта. Для получения простой импликанты выбирается покрытие наибольшего размера.

Для построения минимальной ДНФ по карте Карно следуют двум правилам.

1. Выбирают покрытия наибольшего размера, содержащие ячейки, которые не могут быть ни в каком другом покрытии.

2. Для оставшихся ячеек выбирают покрытие наибольшего размера.

Пример 3.15. Найдем минимальную ДНФ для функции.

=

Выпишем двоичные номера всех K¹:

0000, 0001, 0010, 0011, 0100, 0110, 0111, 1000, 1001, 1011, 1111.

П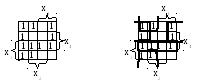остроим карту Карно и покроем все единицы на карте Карно покрытиями наибольшего размера.

Порядок построения минимальной ДНФ будет таким:

• Выбираем покрытие наибольшего размера для ячейки, соответствующей x₁x₂x₃x₄. Это будет импликанта x₃x₄.

• Выбираем покрытие для ячейки 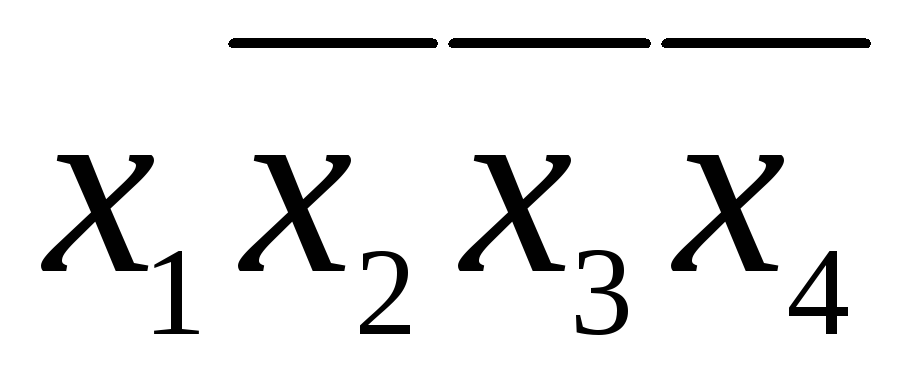. Это будет импликанта.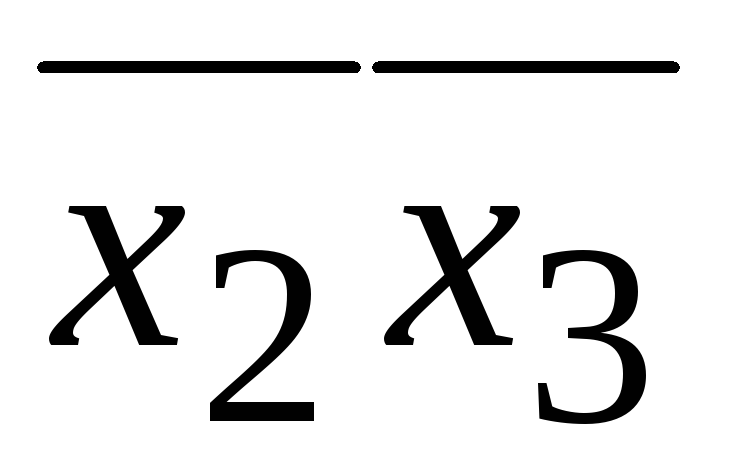

• Выбираем покрытие для ячейки 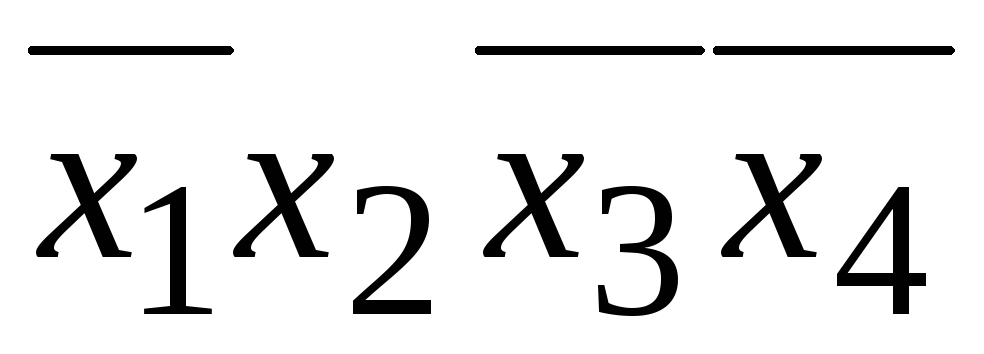. Это будет импликанта.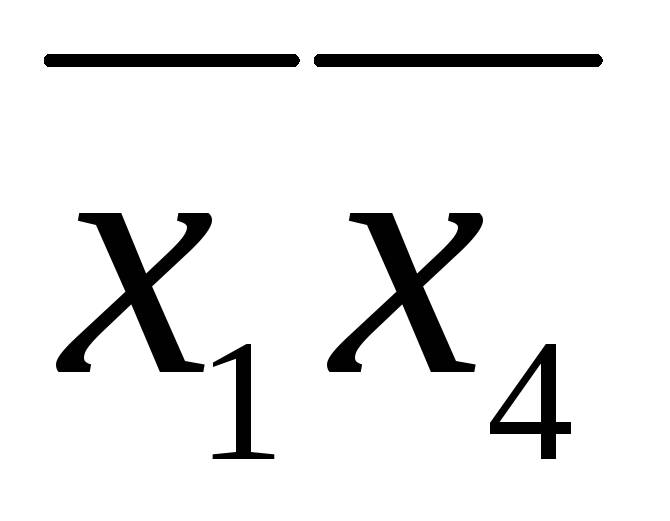

Больше непокрытых ячеек не осталось, следовательно, минимальная ДНФ имеет вид .

7. Булева алгебра и переключательные схемы

Первый опыт применения булевой алгебры был связан с релейными цепями. Хотя эти цепи уже не используются в ЭВМ, они находят применение в ряде систем управления движением.

Контактная цепь – устройство из проводов и контактов, связывающих два полюса. Любой контакт может быть либо замкнут, либо разомкнут. Контакты будем обозначать x₁, x₂, x₃,…

Функция, реализуемая контактной цепью, принимает значение 1, если контур между двумя полюсами замкнут, и 0 – в противном случае. Основные операции булевой алгебры: конъюнкцию, дизъюнкцию и отрицание можно реализовать следующими контактными цепями.

Схема Булева операция

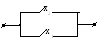
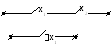x₁x₂

x₁

Соответствие между схемой и булевой операцией легко проверить, сравнив работу схемы с таблицей истинности булевой функции. Операции булевой алгебры представляют цепь без указания направления цепи. Это согласуется с тем, что релейные контакты обладают двусторонней проводимостью. Для сложных контактных цепей можно построить более простую реализацию, упростив исходную булеву функцию с помощью аксиом булевой алгебры или применив один из методов минимизации булевой функции.

Пример 3.16. Упростить схему до пяти контактов.

С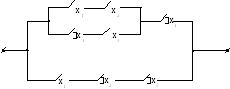оставим булеву функцию для исходной цепи и упростим ее.

.

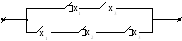По упрощенной формуле составим упрощенную цепь.

Большинство электронных переключательных элементов обладают односторонней проводимостью. Такие элементы реализуют операции булевой алгебры. Они имеют входы, на которые могут подаваться 0 или 1, и выход, на котором может появляться 0 или 1. Такие элементы называются логическими.

Логический элемент Булева операция

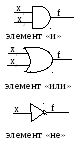
x₁x₂

x₁

Входы одних логических элементов можно подсоединить к выходам других элементов и получить логическую сеть. Логическая сеть реализует некоторую булеву функцию. В случае контактных цепей выражение для функции с наименьшим числом вхождений переменных дает реализацию цепи с наименьшим количеством контактов. Простота логической сети может определяться как числом логических элементов, так и числом входов логических элементов. Кроме того, логические элементы характеризуются запаздыванием, поэтому быстродействие сети пропорционально числу ступеней сети (т.е. максимальному числу логических элементов, через которые проходит входной сигнал без учета инверторов). Представление функции в ДНФ дает двухступенчатую быстродействующую реализацию. Поэтому, для упрощения логической сети можно использовать минимизацию булевой функции методом Квайна, но при этом ввести понятие «стоимости» простой импликанты. В задаче минимизации числа логических элементов стоимость простой импликанты, содержащей две и более переменные, принимается равной 1, а стоимость простой импликанты из одной переменной – 0 (т.к. для ее реализации не требуется логический элемент «и»). В задаче минимизации общего числа входов логических элементов стоимость простой импликанты складывает из входов логического элемента «и», реализующего импликанту, и входов логического элемента «или». При построении минимальной ДНФ по множеству простых импликант, среди простых импликант выбирается множество с суммарной минимальной стоимостью простых импликант.

4. Теория графов

Часто бывает полезно и наглядно изобразить некоторую ситуацию в виде рисунка, состоящего из точек (вершин), представляющих основные элементы ситуации и линий (ребер), отражающих связи между элементами. Такие рисунки называются графами.

Граф может изображать сеть улиц в городе (вершины – перекрестки, улицы – ребра), блок-схемы программ (вершины – блоки, ребра – переходы), электрические цепи, географические карты и т.д. Более точно, граф определяется как упорядоченная пара (V, E), где V – непустое множество вершин, - множество ребер. Граф будем обозначатьG. Число вершин графа называется его порядком и обозначается , число ребер обозначается как .Вершины u и v называются смежными, если существует ребро их соединяющее. Вершина v и ребро e инцидентны, если v является концом е.

Пример 4.1.

Вершины v₁ и v₂ являются смежными,

вершина v₁ инцидента ребрам (v_1, v₂) и (v_1, v₃). .

Граф называется полным, если любые две его вершины смежны. Такие графы обозначаются K_n.

Пример 4.2.

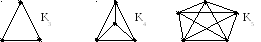
Различные ребра графа могут быть инцидентны одной и той же паре вершин, в этом случае они называются кратными, а сам граф –мультиграфом. Ребро может соединять вершину саму с собой, тогда такое ребро называетсяпетлей, а граф –псевдографом. В некоторых задачах инцидентные ребру вершины рассматриваются в определенном порядке, тогда ребру приписывается направление от одной вершины к другой, и ребро называетсядугой. Граф, все ребра которого являются дугами, называетсяорграфом. Иногда ребрам и дугам графа приписывают некоторые числа, такой граф называетсявзвешенным.

Граф называется помеченным, если всем его вершинам присвоены некоторые метки 1,2,…,n. Степенью вершины v называется число инцидентных ей ребер. Степень вершины обозначается deg v.

Пример 4.3.

Лемма ("о рукопожатиях"). Сумма степеней всех вершин графа равна удвоенному числу его ребер, т.е.

Последовательность степеней вершин графа, записанных в каком-либо порядке, называется степенной последовательностью.

Пример 4.4.

Н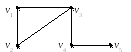айдем степенную последовательность для графаG.

Выпишем степени всех вершин графа в соответствии с их номерами (2,2,3,2,1).

1. Способы задания графов

Пусть G – помеченный граф с n вершинами и m ребрами. Определим матрицу смежности A(G) следующим образом:

Матрица смежности квадратная, размера n  n.

Пример 4.5.

Можно заметить, что матрица смежности является симметричной, и количество единиц в каждой строке равно степени вершины, которой соответствует эта строка. По матрице смежности легко построить графическое представление графа.

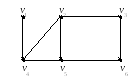
Пример 4.6. Построить граф по матрице смежности

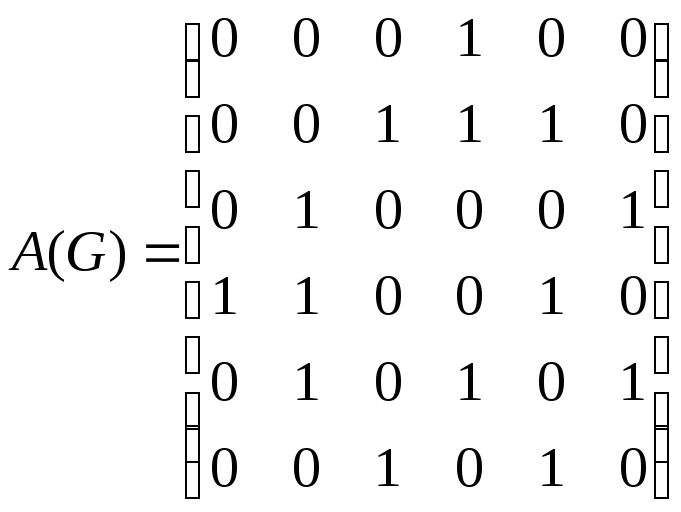
Можно определить матрицу инцидентности I(G), имеющую n строк и m столбцов, элементы которой задаются следующим образом:

Пример 4.7. Рассмотрим граф из примера 4.6, обозначив ребра.

В каждой строке матрицы инцидентности только два элемента отличные от 0 (или один, если ребро является петлей). Поэтому такой способ описания оказывается неэкономным. Отношение инцидентности можно задать также списком ребер графа. Каждая строка этого списка соответствует ребру, в ней записаны номера вершин, инцидентных ему.

Пример 4.8. Рассмотрим граф из примера 4.7. Список ребер имеет вид:

, ,, ,,,.

По списку ребер графа легко построить матрицу инцидентности, т.к. каждое ребро этого списка соответствует столбцу матрицы, а номера вершин в каждом элементе списка – это номера элементов строки матрицы инцидентности, которые равные 1.

Граф может быть представлен различными способами. Иногда не легко понять, одинаковы ли графы, изображенные разными чертежами или разными матрицами. Графы, отличающиеся только нумерацией вершин, называются изоморфными. Перенумерация задается строкой новых номеров вершин, расположенных в исходном порядке. Новая матрица смежности получается в результате перемещения каждого элемента a_ij в строку истолбец, т.е. в результате перестановки () строк и столбцов исходной матрицы. Можно выполнить все возможные перестановки строк и столбцов для того, чтобы убедиться в неизоморфности графов, но это потребуетn! перестановок, что достаточно трудоемко.

2. Маршруты, цепи, циклы

Маршрутом от вершины u к вершине v или (u,v) маршрутом в графе G называется всякая последовательность вида

,

где e_k – ребро, соединяющее вершины и В случае орграфа – началоребра е_k , a v_k – его конец. При этом вершину u называют началом маршрута, а вершину v – его концом. В маршруте некоторые вершины и ребра могут совпадать. Маршрут можно задавать последовательностью вершин а также последовательностью ребер. Число ребер в маршруте называется егодлиной. Маршрут называется цепью, если в нем нет совпадающих ребер, и простой цепью – если дополнительно нет совпадающих вершин, кроме, может быть, начала и конца цепи. Если начало цепи (простой цепи) совпадает с ее концом, то такая цепь называется циклом (простым циклом). Граф без циклов называется ациклическим.

Пример 4.9.

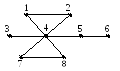(1,2,4,7) – простая цепь;

(1,2,4,7,8,4) – цепь, не являющаяся простой;

(1,2,4,7,8,4,2) – маршрут, не являющийся цепью;

(1,2,4,7,8,4,1) – цикл, не являющийся простым;

(1,2,4,1) – простой цикл.

Граф называется связным, если любые две вершины u и v в нем можно соединить (u,v) маршрутом. Легко видеть, что отношение связности на множестве вершин является отношением эквивалентности. Данное отношение разбивает множество вершин графа на классы, объединяющие вершины, которые можно связать друг с другом маршрутом. Такие классы называются компонентами связности. Связный граф имеет одну компоненту связности.

Пример 4.10.