Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Омский Государственный Университет Путей Сообщения

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Типовик 2 семестр ч5

.pdf

Скачиваний:

Добавлен:

10.04.2015

Размер:

496.81 Кб

Скачать

☆

1 / 41 2 3 4 > Следующая >>>

ГЛАВА 1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

133

3 уровень							11 3 3 x2 23
	x2dx			dx		4
а) 2		;	б) 2		;	в) 4		dx.
	4x2 1 1			x3 8 1 x2			6 x13

Вариант 30

1. Вычислить интегралы непосредственным интегри рованием:

1 уровень
а) 130x dx;						б) 17tgxdx; в) 2(x30 1 cosx)dx;
2 уровень
а)	4	1	ex	3	1			2	dx;	б)	8	1	30sinx 3	4
					1							4
					sin2 x							4		x x
					sin2 x							6		x x
	8	1	30			3	8x x 2
в)		4								5dx.
в)		4		3 25					x2	5dx.
		6 x2		3 25					x2	7

3 уровень

г) 1		x9		dx.
	x	2
			x

5dx;

	3	x	3	1 x 1 x	3	2 x	4		б) 9	1	3e	x	4	15			2
а)								dx;		5								6dx.
														81x	2	3
				x2
										7							81 8

2. Вычислить интегралы, используя метод линейной замены:

1 уровень

а) 1	dx		; б) 2219x dx; в) 1 tg30xdx;		г) 2		dx
								.
	cos2 30x
	cos2 30x					3 1 7x
2 уровень
а) 3(sin30x 2 e13x )dx;				б) 2cos(30 1 2x)dx;	в) 2		dx			.
а) 3(sin30x 2 e13x )dx;				б) 2cos(30 1 2x)dx;	в) 2		111		30x	.
							111		30x
3 уровень
3			ctg(3 3 x)
а) 512235x		4		4 e4x 3 ch30x2dx;
а) 512235x		4	30	4 e4x 3 ch30x2dx;

б) 51 (9 3 2x)11 4 e436x 4 530x39 2dx.

134ПРАКТИКУМ И ЗАДАНИЯ ПО ИНТЕГРАЛЬНОМУ ИСЧИСЛЕНИЮ

3.Вычислить интегралы, используя метод замены пе ременной:

1 уровень

а) 2x6 1 1 x2 dx;				б) 2x2 x3 1 30dx;				в) 2e1 cosx sinxdx.
2 уровень
	sh3 x				3xdx			1arcctgx
а) 1	3 x2 dx;			б) 2		;		в) 3 301 2 x2 dx.
а) 1	3 x2 dx;			б) 2	(x2 1 8)2	;		в) 3 301 2 x2 dx.
3 уровень
а) 2	tg9x 1 30	dx;		б) 2	arccos6 x 1 30		dx;
					1 1 x2
	cos2 x				1 1 x2
в) 3	2x 1 arctg3x		dx.
в) 3	1 2 x2		dx.

4. Вычислить интегралы, используя метод интегриро вания по частям:

1 уровень

а) 1 x30x dx;

б)

1 xcos30xdx;

в) 1 ln30xdx.

2 уровень

а) 2(x 1 5)sin4xdx;

б)

1 x2 x lnxdx;

в) 2arctg 30x 11dx.

3 уровень

а) 1 e2x sinxdx; б) 1 x2e3xdx;

в) 1 x3 x ln2 xdx.

5. Вычислить интегралы от рациональных дробей:

1 уровень

а) 2

в) 3

;

б)

;

x2 1 8x 117

x2 1 4x 112

(x 1 4)(x 2 8)

2 уровень

а) 3

x 1 3

в) 3

2x 1 3

dx;

б)

;

dx.

x(x 21)2

x2 17x 213

x3 1100x

ГЛАВА 1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

135

3 уровень

а) 3

x4 11

dx;

б) 2

dx;

x3 2 x2 1 x 1 1

x3 1 2x2 1 x 1 2

в) 2

x4 1 2x2 1 37

6. Вычислить интегралы от тригонометрических функ

ций:

1 уровень

а) 1 sin5xsin9xdx;

б) 2

;

в) 1 cos5 xsinxdx.

9 1 4sinx

2 уровень

а) 1 sin

б) 1

sin5 x

в) 3

2 1 sinx

8xdx;

cosx dx;

2 2 cosx dx.

3 уровень

а) 2(11 cos3x)3 dx;

б) 1 tg6xdx;

в) 1

sin3 xcosx

7. Вычислить интегралы от иррациональных функций:

1 уровень

а) 2

; б) 2

;

в) 2

1 10x 1

x 1

x x 1

2 уровень

а) 3

x 12

dx;

б) 3

23 1 x2 2 6xdx; в) 2

524x 24x2

x2 1 49

3 уровень

а) 3

4x 11 2 2

dx; б) 2

3 11 x3

(4x 11)2 1 4x 11

dx;

в) 4

3 11 3 5 x4 22

dx.

3 7

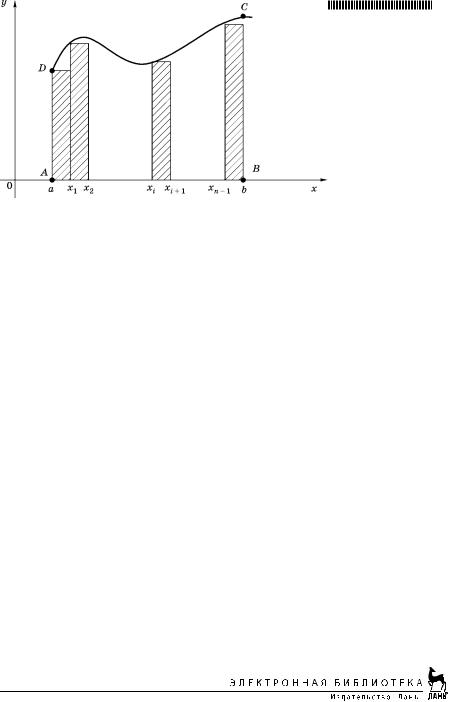
Г Л А В А В Т О Р А Я

ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

2.1.

ЗАДАЧА О ПЛОЩАДИ КРИВОЛИНЕЙНОЙ ТРАПЕЦИИ

Рассмотрим криволинейную трапецию ABCD (рис. 2), т. е. фигуру, ограниченную сверху графиком функции у = f(x) (уравнение линии DC), снизу — осью Ox, сбоку — прямы ми x = a и у = b. Найдем площадь этой трапеции. Разде лим основание АВ данной фигуры произвольным образом на части и проведем ординаты, соответствующие точкам деления. Тогда криволинейная трапеция разобьется на ряд прямоугольников (рис. 2).

Обозначим точки деления:

a = x0 < x1 < x2 < ... < xi < xi+1 < ... < xn–1 < xn = b. (13)

Основание i го прямоугольника (i = 0, 1, 2, ..., n – 1), очевидно, равно разности xi+1 – xi, которую обозначим че

Рис. 2

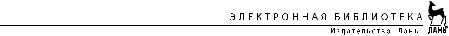
Погрешность этого равенства при безграничном убы вании всех xi стремится к нулю. Точное значение площа ди получится как предел:

ГЛАВА 2. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

137

рез xi. Высота, следовательно, равна yi = f(xi), поэтому площадь i го прямоугольника равна yi xi = f(xi) xi.

Просуммировав площади всех прямоугольников, по лучим приближенное значение площади P криволинейной

трапеции:	n11	n11
P 3	5yi 4xi 2	5f(xi )4xi .
	i20	i20

		n11			n11
P 4 lim		5	yi 2xi 4 lim		5	f(xi )2xi ,	(14)
2x	30	5	2x	30	5
i		i40	i		i40

в предположении, что все xi одновременно стремятся к нулю. Для предельного значения суммы (14) введено обо

значение 1 f(x)dx — в случае площади фиксированной

фигуры ABCD, отвечающей изменению x от a до b.

2.2.

ПОНЯТИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА

Пусть f(x) определена на отрезке [a, b]. Разделим отре зок [a, b] на n произвольных частей точками a = x0 < x1 < < x2 < ... < xn–1 < xn = b, выберем на каждом элементарном отрезке [xk–1, xk] произвольную точку zk и найдем длину каждого такого отрезка: xk = xk – xk–1.

Определение 2.1. Интегральной суммой для функции f(x) на отрезке [a, b] называется сумма вида (см. рис. 3)

4f(zk )2xk 1 f(z1 )2x1 3 f(z2 )2x2 3 ... 3 f(zn )2xn . (15)

k11

Обозначим через = max xk. Предположим, что после довательность интегральных сумм стремится к некоторо му пределу:

lim 6f(zk )5xk 3 S. (*)

n12 k31 (410)

138	ПРАКТИКУМ И ЗАДАНИЯ ПО ИНТЕГРАЛЬНОМУ ИСЧИСЛЕНИЮ

Рис. 3

Определение 2.2. Если существует предел (*), не зави сящий от способа разбиения отрезка [a, b] и выбора то чек zk, то этот предел называется определенным интегра? лом от функции f(x) на отрезке [a, b] (в пределах от a до b):

b		n
7f(x)dx 3	lim	6f(zk )5xk.	(16)
7f(x)dx 3	lim	6f(zk )5xk.
a	n12 k31
	(410)

При этом f(x) — интегрируемая функция на [a, b] (по дынтегральная функция); f(x)dx — подынтегральное вы ражение; a, b — пределы интегрирования (a — нижний предел, b — верхний предел), отрезок [a, b] называется от резком интегрирования; x — переменная интегрирования.

Учитывая рассуждения, приведенные в п. 2.1, можно сделать вывод о том, что определенный интеграл от неот рицательной интегрируемой функции численно равен пло щади криволинейной трапеции.

Теорема 2.1 (о существовании определенного интеграла). Если функция f(x) непрерывна на отрезке [a, b], то она

интегрируема на отрезке [a, b].

Непрерывность функции является достаточным усло вием ее интегрируемости, но не является необходимым. Так определенный интеграл может существовать и для некоторых разрывных функций.

ГЛАВА 2. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

139

Отметим, что в отличие от неопределенного интегра ла, определенный интеграл для фиксированных значе ний a и b — число.

Например, если производительность труда, т. е. объ ем продукции, произведенной в единицу времени, явля ется непрерывной функцией от времени t, то объем вы пускаемой продукции за промежуток времени [0, T] вы

числяется по формуле

Q 1 2f(t)dt.

2.3. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

КАК ФУНКЦИЯ ВЕРХНЕГО ПРЕДЕЛА

Если функция f(x) интегрируема в промежутке [a, b], то она интегрируема и в промежутке [a, x], где x — любое значение из отрезка [a, b]. Рассмотрим функцию

x
1(x) 2 3f(t)dt.	(17)

Эта функция обладает следующими свойствами:

1)если функция f(x) интегрируема на [a, b], то (x) бу дет непрерывной функцией от x в том же промежутке;

2)если функция f(x) непрерывна на [a, b], то в любой

точке x [a, b] функция (x) имеет производную, равную f(x): (x) = f(x).

Таким образом, функция (x), определенная равенством (17), является одной из первообразных функции f(x) на [a, b].

2.4.

ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА С ПОМОЩЬЮ ФОРМУЛЫ НЬЮТОНА — ЛЕЙБНИЦА

Пусть функция f(x) непрерывна на [a, b], а F(x) — одна из первообразных для f(x) на отрезке [a, b], т. е. F (x) = f(x), тогда справедлива формула Ньютона — Лейбница

3f(x)dx 1 F(x) ba

1 F(b) 2 F(a).

(18)

140	ПРАКТИКУМ И ЗАДАНИЯ ПО ИНТЕГРАЛЬНОМУ ИСЧИСЛЕНИЮ

Таким образом, чтобы вычислить определенный инте грал по данной формуле, необходимо:

1)проверить, что функция f(x) непрерывна на отрез ке [a, b];

2)найти первообразную подынтегральной функции f(x);

3)воспользоваться формулой Ньютона — Лейбница. Отметим, что Исаак Ньютон(1643–1727) — англий

ский физик, математик и астроном, один из создателей классической физики, Готфрид Вильгельм фон Лейбниц (1646–1716) — немецкий философ, математик, юрист, дипломат. Именно Лейбниц ввел знак интеграла: ради сокращения записи он вводит начальную букву слова Summa, которая по начертанию того времени писалась как 1 (1675). До этого в первой половине XVII в. при вы числении площади фигуры операцию записывали слова ми: «совокупность всех неделимых». Слово «интеграл» употребил впервые Якоб Бернулли в 1690 г. (швейцарский математик, 1654–1705). Возможно, термин образован от латинского integer (целый). По другому предположению, Я. Бернулли произвел термин от integro (приводить в преж нее состояние, восстанавливать), действительно, восста навливается первообразная функция. Термин был обсуж ден Иоганном Бернулли (швейцарский математик, млад ший брат Якоба, 1667–1748) и Лейбницем и «принят» в 1696 г. Тогда же И. Бернулли предложил название инте гральное исчисление (calculus integralis). Он пояснил, что, по его мнению, дифференциал — это бесконечно малая часть целого, интеграла (см. подробно [1]).

Пример 2.1.

1 x2dx.

Р е ш е н и е. Подынтегральная функция x2 непрерыв на на промежутке интегрирования, поэтому формулой Нью тона — Лейбница пользоваться можно:

1	2	x3	1	1	1

2x dx 1 3			0		3.
0

ГЛАВА 2. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

141

Пример 2.2.			1 /4
			1 /4		dx
			2		dx	.
			2		2	.
			1 /6 cos x
								1
Р е ш е н и е. Подынтегральная функция											непре
Р е ш е н и е. Подынтегральная функция									cos2 x		непре
рывна на промежутке интегрирования, поэтому
1 /4	dx			1 /4	2 tg 1 3 tg 1 2 1 3			3
		2 tgx								.


4 cos2 x				1 /6	4		6	3
1 /6

Пример 2.3.

2 dx.

11 x2

Р е ш е н и е. Здесь подынтегральная функция x2 тер

пит разрыв в точке x = 0. Поэтому формулой Ньютона — Лейбница в данном примере воспользоваться нельзя, одна ко выражения такого типа имеют определенный смысл, ко торый рассмотрим в дальнейшем (см. п. 2.8.2, пример 2.14).

2.5. ОСНОВНЫЕ СВОЙСТВА

ОПРЕДЕЛЕННОГО ИНТЕГРАЛА

b a

1.3f(x)dx 1 23f(x)dx.

a	b
a
2. 2f(x)dx 1 0.
a
b	c	b

3. 3f(x)dx 1 3f(x)dx 2 3f(x)dx.

a	a	c
b	b	b

4. 3[f1 (x) 1 f2 (x)]dx 2 3f1 (x)dx 1 3f2 (x)dx.

a a a

b b

5.2Cf(x)dx 1 C2f(x)dx.

142 ПРАКТИКУМ И ЗАДАНИЯ ПО ИНТЕГРАЛЬНОМУ ИСЧИСЛЕНИЮ

6. Оценка определенного интеграла: если m f(x) M

на [a, b], то

m(b 1 a) 2 3f(x)dx 2 M(b 1 a).

7. Если f(x) четная функция, то

3 f(x)dx 2 23f(x)dx.

8. Если f(x) нечетная функция, то

3 f(x)dx 2 0.

Пример 2.4.

3 ex2 x3dx 2 0,

поскольку подынтегральная функция — нечетная.

Пример 2.5.

3/2	3/2	03/2 2 5 21sin 23 4 sin02 5 261 5 2,
7	cosxdx 5 2 7 cosxdx 5 21sinx


43/2	0
так как подынтегральная функция — четная.
	2.6.
	ЗАМЕНА ПЕРЕМЕННОЙ
	В ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ

Если функция f(x) непрерывна на отрезке [a, b], а функция x = (t) непрерывна вместе со своей производ

ной (t) на [t1, t2], множеством значений функции x = (t)
при t [t1, t2] является отрезок [a, b], причем если a = (t1),
b = (t2), то	b	t2
	4f(x)dx 2 4 f(3(t))31(t)dt.		(19)

at1

Порядок вычисления:

1) ввести новую переменную с помощью подстановки вида x = (t) или t = (x). Выбор подходящей переменной см. по п. 1.4.1 (табл. 2), п. 1.6, 1.7;

1 / 41 2 3 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
09.04.2015203.26 Кб599Технол карты тек рем обор подст.doc
#
10.04.20151.02 Mб89Технологическая карта 2.2.docx
#
10.04.2015520.51 Кб16Типовик 2 семестр ч2.pdf
#
10.04.2015354.1 Кб17Типовик 2 семестр ч3.pdf
#
10.04.2015360.76 Кб5Типовик 2 семестр ч4.pdf
#
10.04.2015496.81 Кб6Типовик 2 семестр ч5.pdf
#
28.04.201946.59 Кб2ТИПОВОЕ ПОЛОЖЕНИЕ о мол. спеце Дочерних иЗависи....doc
#
09.04.2015354.82 Кб31Типовой расчёт 3.doc
#
10.04.20151.22 Mб14типовой расчет.doc
#
18.09.201984.99 Кб10тире в простых предложениях. Булгаков Собачье с...doc
#
10.04.201524.58 Кб25титульник для реферата.doc