§14.3. Интегрирование иррациональных функций

14.3.1.Интегрирование выражений

В дальнейшем важным приемом интегрирования будет использование таких подстановок , которые приводят подынтегральное выражение к рациональному виду, в результате чего интеграл вычисляется в виде функции от . Если при этом сама функция , которую надлежит подставить вместо , выражается через элементарные функции, то интеграл представит

собой элементарную функцию от .

В качестве первого примера рассмотрим интеграл вида

,

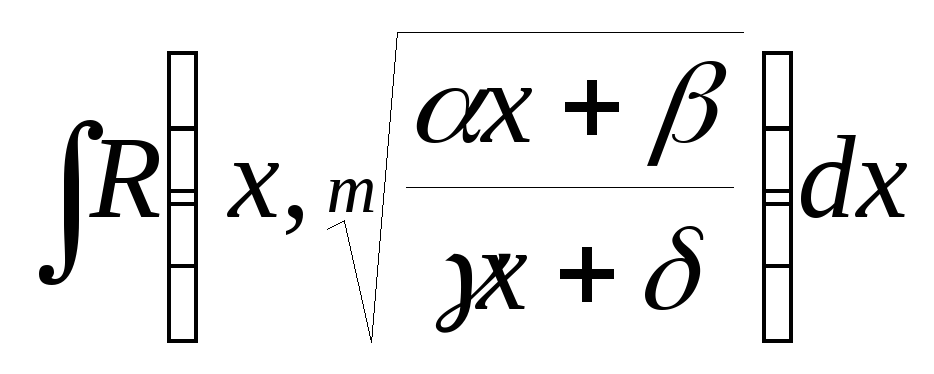где рациональная функция, т.е. отношение многочленов от двух аргументов, - натуральное число, а - постоянные. (Напомним, что многочленом от двух аргументов называется конечная сумма одночленов вида, где неотрицательные целые числа, .)

Положим

, , .

При такой замене интеграл перейдет в

;

Здесь подынтегральное выражение- рациональная функция от , поскольку рациональные функции от . Вычислив этот интеграл по правилам предыдущего параграфа, вернемся к старой переменной, подставив .

К интегралу рассмотренного вида сводятся и более общие интегралы

,

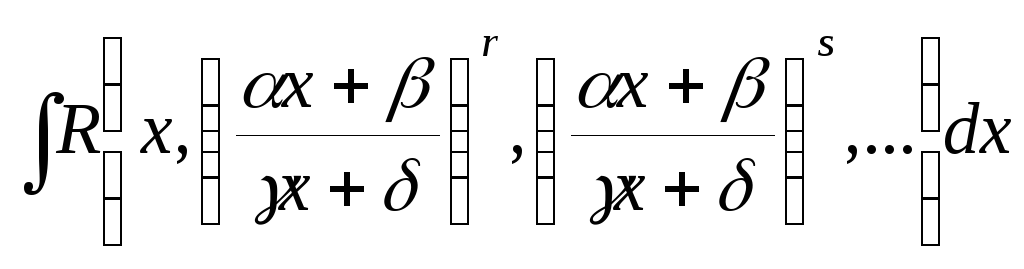в которых все показатели степеней - рациональные числа. Для этого требуется привести все эти показатели к общему знаменателю , чтобы под знаком интеграла получить рациональную функцию от радикала .

Пример. Найти интеграл

.

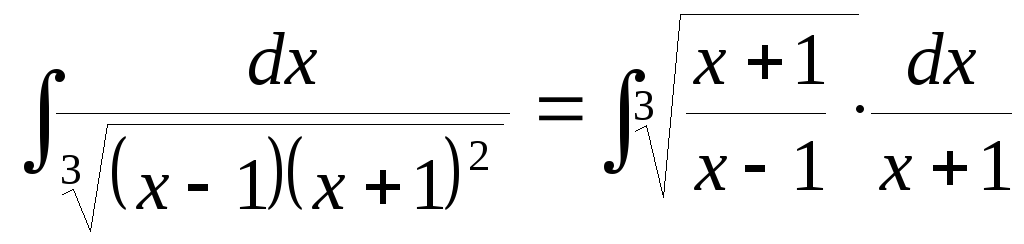Полагаем , , ; тогда ,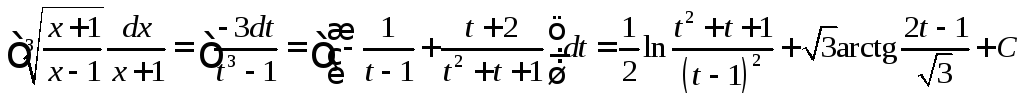

где .

14.3.2.Интегрирование выражений вида . Подстановки Эйлера

Переходим к рассмотрению очень важного класса интегралов

.

Предполагаем, конечно, что квадратный трёхчлен не имеет действительных корней. В противном случае можно использовать метод предыдущего пункта.

Мы изучим подстановку, называемую подстановкой Эйлера, с помощью которой можно достигнуть рационализации подынтегрального выражения .

Подстановка приложима в случае, если . Тогда полагают . Возводя это равенство в квадрат, найдём , , так что

, ,

.

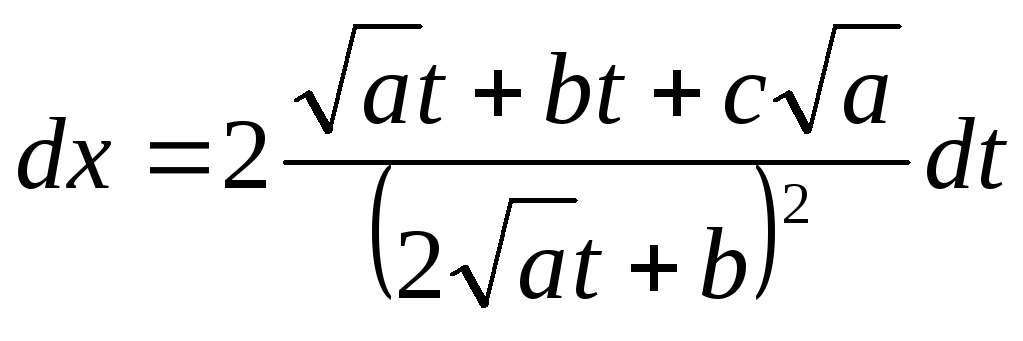Таким образом, для определения получается уравнение первой степени , так что , а одновременно с ним также и радикал выражаются рационально через . В результате, возвращаясь к , нужно будет положить

§14.4. Интегрирование тригонометрических функций

14.4.1. Интегралы вида

Для интегралов этого вида существует универсальная тригонометрическая подстановка . При этом

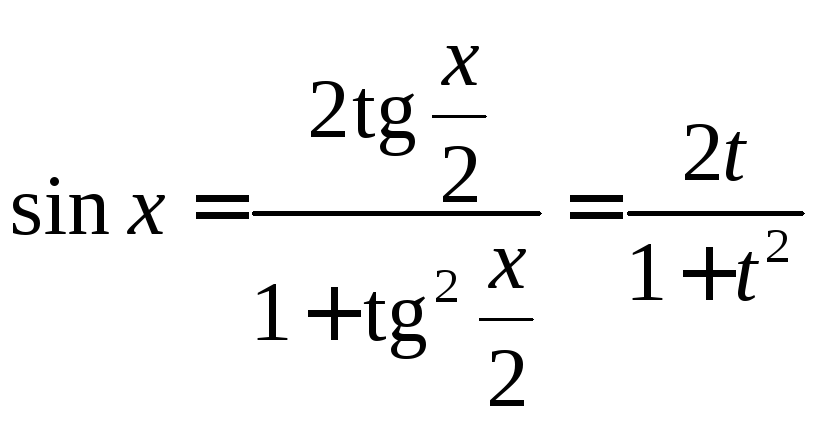, , , так что

.

Таким образом, интегралы типа

всегда берутся в конечном виде.

Универсальная для интеграла рассматриваемого типа тригонометрическая подстановка часто приводит к сложным вычислениям. Для некоторых интегралов можно использовать более простые подстановки.

Сформулируем без доказательства утверждение( относящееся к курсу алгебры)

Утверждение. Если рациональная функция не меняет своего значения при изменении знака одного из аргументов, например, , т.е. если

то она может быть приведена к виду

,

содержащему лишь чётные степени .

Если же, наоборот, при изменении знака функция также меняет знак, т.е. если , то она приводится к виду

;

(Это сразу вытекает из предыдущего утверждения, если его применить к функции .)

Пусть теперь меняет знак при изменении знака ; Тогда

,

и используется подстановка .

Аналогично, если меняет знак при изменении знака , то , так что здесь целесообразна подстановка .

Предположим, что функция не меняет своего значения при одновременном изменении знаков и , .

В этом случае, заменяя на , будем иметь .

По свойству функции , если изменить знаки и (отношение при этом не изменится),

, а тогда

_. Поэтому

, т.е. .

Здесь используем подстановку , так как

.

Замечание.Любую рациональную функцию двух переменных можно представить в виде суммы:

Первое из этих слагаемых меняет знак при изменении знака , второе меняет знак при изменении знака , а третье сохраняет значение при одновременном изменении знака и . Разбив выражение на соответствующие слагаемые, можно к первому из них применить подстановку , ко второму подстановку - и, наконец, к третьему – подстановку типа.

14.4.2. Интегралы вида , ,

Для вычисления интегралов.

, ,

используются формулы

,

,

.

После их использования рассматриваемые интегралы сразу сводятся к табличным.

Приложение