Тема 8. Непрерывные случайные величины

Случайная величина ξ называется непрерывной, если ее функция распределения F(х) = P{ < x} непрерывна и дифференцируема для всех хR, за исключением, быть может, конечного или счетного числа точек.

Функция

р(х) = F '(х) = 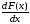(8.1)

называется плотностью распределения (вероятностей) непрерывной с.в. ξ.

Закон распределения непрерывной с.в.  может задаваться, наряду с ее функцией распределения F(х), также и плотностью распределения р(х), поскольку, исходя из плотности распределения р(х), можем найти ф.р. F(х) по формуле

F(х) = 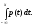(8.2)

Функция распределения F(x) непрерывной с.в.  обладает свойствами, аналогичными свойствам функции распределения дискретной с.в. (кроме свойства 3⁰):

1⁰) определена при всех xR и 0  F(x)  1;

2⁰) является неубывающей функцией:

если x₁ < x₂, то F(x₁)  F(x₂);

3⁰) является непрерывной функцией:

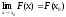для всех x₀R;

4⁰) удовлетворяет предельным соотношениям:

.

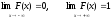Плотность распределения р(х) обладает следующими основными (характеристическими) свойствами.

1. Плотность распределения является неотрицательной функцией:

р(х)  0 для всех х  R. (8.3)

2. Площадь фигуры, ограниченной графиком плотности распределения и осью абсцисс, равна единице:

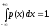(8.4)

Теорема. Пусть непрерывная с.в. ξ имеет плотность распределения р(х) и функцию распределения F(х). Обозначим через <х₁, х₂> один из интервалов (конечный или бесконечный) вида [х₁, х₂], [х₁, х₂), (х₁, х₂], (х₁, х₂). Тогда

Р{ξ<х₁, х₂>} = F(х₂) – F(х₁) =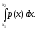 (8.5)

Замечание. Из этой теоремы вытекает, в частности, что если плотность распределения р(х) с.в. ξ нулевая (или функция распределения F(х) постоянна) на некотором интервале <х₁, х₂>, то с.в. ξ не принимает там значений: P{<x₁, x₂>} = 0.

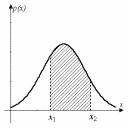
Рис.8.1. Графическая интерпретация

вероятности P{< x₁, x₂ >}

Вторая часть формулы (8.5) имеет следующий геометрический смысл: вероятность P{<x₁, x₂>} равна площади криволинейной трапеции, ограниченной графиком плотности распределения p(x), осью абсцисс и прямыми x = x₁, x = x₂ (на рис. 8.1 заштрихованная область).

Математическим ожиданием (средним значением) непрерывной с.в. ξ с плотностью распределения р(х) называется величина

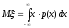. (8.6)

При этом предполагается, что интеграл в правой части формулы (8.6) абсолютно сходится, т.е.

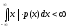. (8.7)

В противном случае говорят, что математического ожидания у с.в. ξ не существует.

В частности, если все возможные значения непрерывной с.в. ξ принадлежат конечному интервалу (a,b), т.е.p(x) = 0 приx (a,b), то условие (8.7) выполняется и всегда существует

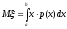. (8.8)

Дисперсией непрерывной с.в. ξ называется величина Dξ, определяемая равенством

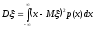,(8.9)

или равносильным равенством

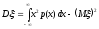.(8.10)

В частности, если все возможные значения непрерывной с.в. ξ принадлежат интервалу (a, b), то

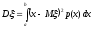,(8.11)

или

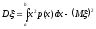.(8.12)

Среднее квадратическое (или стандартное) отклонение непрерывной с.в.  определяется так же, как и для дискретной с.в.: .

Математическое ожидание и дисперсия непрерывных с.в. обладают теми же свойствами, что и для дискретных с.в. (см. тему 7).

Пример 8.1. При изучении некоторого признака исследователь предположил, что ошибка  (мм) результатов наблюдений над этим признаком является случайной с плотностью распределения

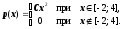
1). При каком значении С исследователь будет прав? Построить график плотности распределения.

2). Найти функцию распределения с.в.  и построить её график.

3). Определить вероятность того, что с.в.  примет значение:

a) меньше 2; b) из промежутка [ – 1; 3]; c) положительное.

Проиллюстрировать вероятности п.п. a), b) и c) на графике плотности распределения.

4). Вычислить математическое ожидание (среднее значение) М, дисперсию D и среднее квадратическое (стандартное) отклонение ().

Решение. 1). Исследователь будет прав, если функция p(x) удовлетворяет характеристическим свойствам (8.3) и (8.4) плотности распределения. Очевидно, условие (8.3) неотрицательности p(x) будет выполнено, если С  0.

В силу свойства (8.4) плотности распределения должно быть выполнено равенство

,

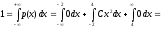
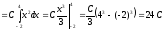откуда С = 1/24.

Таким образом, плотность распределения с.в.  имеет вид

р(х) =

График функции р(х) представлен на рис. 8.2.

2). Для нахождения ф.р. F(х) с.в.  воспользуемся формулой (8.2).

а) Если х < –2, то р(х) = 0 и, следовательно,

F(х) =

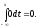
b) Если –2  х  4, то 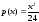и, следовательно,

.

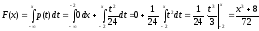c) Если х > 4, то р(х) = 0 и, следовательно,

.

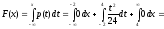
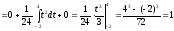Таким образом, искомая функция F(х) имеет вид

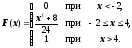
График функции F(х) изображен на рис. 8.2.

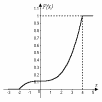
Рис.8.2. Плотность и функция распределения с.в. 

3). I способ (с помощью плотности распределения). Используя вторую часть формулы (8.5) и вид плотности распределения p(x), получаем:

a)

;

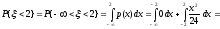
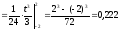b)

;

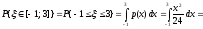
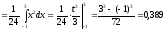c) .

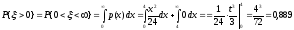Графическое представление вероятностей a), b) и c) приведено на рис. 8.3.

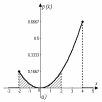
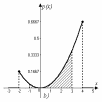
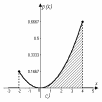
Рис. 8.3.Графическая иллюстрация вероятностей п.п.a), b) и c)

II способ (с помощью функции распределения). Используя первую часть формулы (8.5) и вид функции распределения F(x), находим:

a) P{ < 2} = F(2) = (2³ + 8)/72 = 0,222;

b) P{[– 1; 3]} = F(3) – F(– 1) = (3³ + 8)/72 – ((– 1)³ +8)/72 = 0,389;

c) P{ >0} = P{0 <  < } = F() – F() = 1 – 8/72 = 0,889.

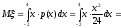
4). Поскольку все возможные значения с.в. ξ принадлежат интервалу [–2; 4] ( p(x) = 0 приx [–2; 4]), то в силу формулы (8.8) имеем

(мм).

Для нахождения дисперсии D вычисляем вначале

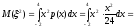
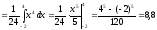(мм²).

Тогда Dξ = М(ξ²) – (Мξ)² = 8,8 – (2,5)² = 2, 55 (мм²) и 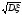() = = 1,597 (мм).

Пример 8.2. Случайная величина  имеет плотность распределения

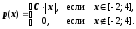
1). Определить неизвестную постоянную С и построить график функции p(x).

2). Найти функцию распределения с.в.  и построить её график.

3). Определить вероятность того, что с.в.  примет значение:

a) меньше 2; b) из промежутка [ – 1; 3]; c) положительное.

Проиллюстрировать вероятности п.п. a), b) и c) на графике плотности распределения.

4). Вычислить математическое ожидание (среднее значение) М, дисперсию D и среднее квадратическое (стандартное) отклонение ().

Решение. 1). Значение постоянной С найдем из условия (8.4) нормировки плотности распределения:

,

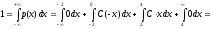
откуда С = 1/10.

Теперь плотность распределения p(x) определена полностью:

График этой функции изображен на рис.8.3.

2). Функцию распределения F(x) с.в.  найдем по формуле (8.2).

а) Если x < – 2, то p(x) = 0 и, следовательно, .

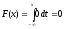b) Если – 2  x < 0, то p(x) = – 0,1 x и

.

с) Если 0  x  4, то p(x) = 0,1 x и

.

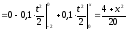d) Если х > 4, то р(х) = 0 и

.

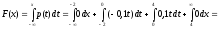
Таким образом, искомая функция F(х) имеет вид

График функции F(x) приведен на рис.8.4.

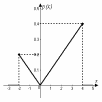
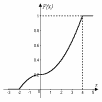
Рис.8.4. Плотность и функция распределения с.в. 

8.3. В некоторых странах действует о налогообложении, который распространяется на тех физических лиц, годовой доход которых превосходит некоторый установленный законом уровень (скажем 25 тысяч у.е.). Рассматривается непрерывная с.в. , равная годовому доходу наудачу выбранного лица, облагаемого доходом, которая имеет функцию распределения

1) Найти неизвестный параметр C и построить график функции F(x).

2) Вычислить средний годовой доход лиц, облагаемых налогом.

3) Определить вероятность того, что у наудачу выбранного лица, облагаемого доходом, доход больше, чем средний годовой доход подобных лиц.

4) Чему равна дисперсия с.в. ?

Решение. 1) Поскольку функция распределения F(x) должна быть непрерывной (рассматривается непрерывная с.в. ), то должно выполняться равенство

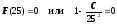, откуда C = 625.

2) Так как

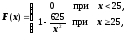
то

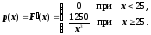
По формуле (8.8) получаем

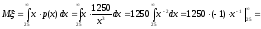
(тыс. у.е.).

3) Искомую вероятность P{ > M} = P{ > 50} найдем с помощью первой части формулы (8.5):

P{ > M} = P{ 50 <  <} = F() – F(50) = 1 – (1 – 625/(50)²) = 0,75.

4) Для нахождения дисперсии D вычислим вначале

.

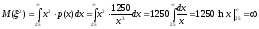Следовательно, Dξ = М(ξ²) – (Мξ)² =  – 50² = , т.е. дисперсии у с.в.  не существует. 

8.4. Плотность распределения случайной величины  имеет вид

Выполнить п.п. 1) – 4) примера 8.2.

8.5. Закон распределения непрерывной случайной величины  задан функцией распределения

,

где a и b – неизвестные постоянные.

1). Исходя из свойств функции распределения, определить неизвестные постоянные a, b и построить график функции F(x).

2). Найти плотность распределения p(x) и построить её график.

3). Определить вероятность того, что с.в.  примет значение:

a) отрицательное; b) из промежутка [– 1; 1]; c) положительное.

Проиллюстрировать вероятности п.п. a), b) и c) на графике плотности распределения.

4). Существуют ли для данной с.в.  математическое ожидание (среднее значение) и дисперсия D?

8.6. Из практики работы телеателье известно, что время  (в днях) ремонта телевизоров является случайным с функцией распределения

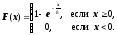
1). Построить график функции распределения F(x).

2). Найти плотность распределения с.в.  и построить её график.

3). Какова вероятность того, что в данном телеателье ремонта телевизора придется ожидать: a) не более пяти дней; b) больше недели?

4). Вычислить среднее значение, дисперсию и стандартное отклонение времени ремонта телевизоров в этом телеателье.

1)¹⁾ В дальнейшем данную операцию будем называть описанием пространства элементарных исходов испытания.

47