Тема 2. Классическое определение вероятности

Если все элементарные исходы испытания являются равновозможными и их число конечно, то вероятность наступления событияАв результате этого испытания равна отношению числаN(A) благоприятствующих событиюАисходов к общему числуN всех элементарных исходов испытания:

P(A) =.

Для применения данного классического определения вероятностинеобходимо вычислить значенияNи N(A). Для того чтобы иметь некоторые стандартные приемы при расчетах по схеме классической вероятности, приведем некоторые сведения из комбинаторики – раздела математики, посвященного решению задач выбора и расположения элементов некоторого множества в соответствии с заданными правилами.

При решении задач комбинаторики используются следующие правила.

Правило умножения.Пусть необходимо выполнить одно за другим какие-тоkдействий. Если первое действие можно выполнитьn₁способами, после чего второе действие можно выполнитьn₂способами, и так доk– го действия, которое можно выполнитьn_kспособами, то всеkдействийвместемогут быть выполненыn₁×n₂×…×n_kспособами.

Правило сложения.Пусть какие-тоkдействий взаимно исключают друг друга. Если первое действие можно выполнитьn₁способами, второе действие –n₂способами, и так доk– го действия, которое можно выполнитьn_kспособами, токакое-либо одноиз них можно выполнитьn₁+n₂+ … +n_kспособами.

Перестановкой из n элементов называется набор изnэлементов, расположенный вопределенном порядке. Две перестановки изnэлементов отличаются друг от друга только порядком своих элементов. Число перестановок изnэлементов равно

P_n =n! = 1·2·3·…·(n– 2)·(n – 1)·n .

По определению полагается

P₀ = 0! = 1.

Размещением из n элементов по kназываетсяупорядоченный наборизkэлементов, выбранных из данныхnэлементов (k£n). Два размещения из nэлементов по kотличаются друг от друга либо порядком, либо составом своих элементов. Число всех возможных размещений изnпоkравно

.

Число всевозможных перестановок из n элементов поk, в которых элементы могутповторяться, равноn^k .

Сочетанием из n элементов по kназываетсянеупорядоченный наборизkэлементов, выбранных из данныхnэлементов (k£n). Два сочетания отличаются друг от друга только составом своих элементов. Число сочетаний изnэлементов поkравно

Приведенные выше сведения из комбинаторики представлены в следующей схеме.

Нет

Нет

Нет

Классическая схема подсчета вероятностей пригодна для решения многих практических задач. Рассмотрим, например, некоторое множество из nэлементов, среди которых по некоторому признаку выделено подмножество изn₁элементов (n₁n), которые назовем “отмеченными”. Это могут быть изделия (годные и бракованные), семена (всхожие и нет) и т. п. Из этого множества элементов наугад без возвращения извлекаютсяkэлементов. Тогда вероятностьтого, что в выборке будет ровноk₁“отмеченных” элементов (k₁k) определяется по формулегипергеометрических вероятностей:

.

Пример 2.1.В примерах 1.2 – 1.9 (тема 1) вычислить вероятности всех событий.

Решение примера 1.2.По классическому определению вероятности

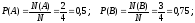
. g

Решение примера 1.3.Здесь мы также имеем классическую схему, согласно которой

.

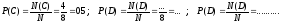Решение примера 1.4.

Пример 2.2.На пяти карточках написаны цифры 1, 2, 3, 4, 5. Наугад берутся три карточки и кладутся в ряд. Чему равна вероятность того, что полученное таким образом трехзначное число окажется: а) не больше 400; b) четным?

Решение (непосредственный подсчет вероятностей).Испытание – извлечение (без возвращения) из 5 карточек трех и расположение их в ряд. Обозначим черезAи Bсобытия, описанные в п.п. а) и b) примера. Пустьi₁– 1-я цифра слева,i₂– 2-я цифра слева иi₃– 3-я цифра слева полученного трехзначного числа. Тогда

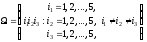и

.

Для нахождения N= N(),N(A) иN(B) воспользуемся правилом умножения. Пустьk-е действие состоит в извлеченииk-й карточки (k= 1, 2, 3). Поскольку карточки берутся без возвращения, то N() = 543 = 60,N(A) = 343 = 36 иN(B) = 243 = 24. Следовательно,

. g

Пример 2.3. Из пяти карточек с буквами А, Б, В, Г, Д наугад одна за другой выбираются три и располагаются в ряд. Какова вероятность того, что получится слово “ДВА”?

Решение (комбинаторный метод вычисления вероятности). Испытание состоит в том, что из пяти карточек последовательно выбираются три и выкладываются в ряд. Число всех элементарных исходов данного испытания – это число всевозможных слов из трех букв (как осмысленных, так и бессмысленных), которые можно составить из имеющихся пяти букв, т.е. число различных упорядоченных комбинаций (размещений) из 5 букв длиной в 3 буквы:

Рассмотрим событие А = {получится слово “ДВА”}. Вероятность этого события вычислим по классическому определению. Из полученныхN =60 всевозможных слов длиной в три буквы благоприятствующим событиюАявляется только одно: слово “ДВА”. Следовательно,N(A) = 1 иg

Пример 2.4.В условиях примера 2.2 имеются три карточки с цифрой 1, две карточки с цифрой 2 и по одной карточке с цифрами 3, 4, 5.

Решение.Испытание –

Пример 2.5.На шести карточках разрезной азбуки написаны 3 буквы А, 2 буквы Н и одна буква С. Ребенок, не умеющий читать, раскладывает эти карточки в ряд. Какова вероятность того, что у него получится слово “АНАНАС”?

Решение.Испытание – выкладывание в ряд 6 букв, что эквивалентно, очевидно, извлечению (без возвращения) из имеющихся карточек шести и расположению их в ряд. Обозначим черезAсобытие, состоящее в том, что получится слово “АНАНАС”.

1-й способ(непосредственный подсчет вероятности).

Пусть x_i–i-я буква слева, полученного слова (осмысленного или бессмысленного),i= 1, 2, …, 6. Тогда

и

.

Воспользовавшись правилом умножения, находим N() = ……………………… иN(A) = ………………………….. Следовательно,P(A) = ……………………………..

2-й способ(комбинаторный метод вычисления вероятности).

Пример 2.6.В лифт девятиэтажного дома на первом этаже вошли 4 человека. Каждый из них (независимо от других) может выйти на любом из этажей, начиная со второго. Найти вероятность того, что:

a) все пассажиры выйдут на разных этажах;

b) все пассажиры выйдут на одном этаже;

с) два пассажира выйдут на одном этаже, а двое других – на разных этажах.

Решение.Испытание ­– выход 4 человек на случайным образом выбираемом каждым из них этаже дома (со 2-го по 9-й). ПустьA,BиC– события, описанные в п.п.a),b) иc).

1-й способ(непосредственный подсчет вероятностей).

2-й способ(комбинаторный метод вычисления вероятностей).

Пример 2.7.За круглым столом случайным образом рассаживаются 10 человек, среди которых находится одна супружеская пара. Определить вероятность того, что муж с женой окажутся рядом.

2.8.В условиях задачи 2.7 люди рассаживаются вдоль одной стороны прямоугольного стола.

2.9.Группа из 6 мальчиков и 6 девочек делится случайным образом на две равные подгруппы. Найти вероятность того, что:

а) в каждой подгруппе число мальчиков и девочек будет одинаковым;

b) в какой-либо подгруппе мальчиков будет больше, чем девочек.

Пример 2.10. Двенадцать человек, среди которых 6 юношей и 6 девушек, случайным образом группируются попарно. Определить вероятность того, что:

а) все десять пар будут состоять из лиц разного пола;

b) будет хотя бы одна пара, состоящая из лиц разного пола.

2.11. Брошены три монеты. Найти вероятности событий:

а) A= {первая монеты выпала гербом};

б) B= {выпало ровна два герба};

в) C= {Выпало не больше двух гербов}.

2.12. Ребенок играет с 10 буквами разрезной азбуки: А, А, А, Е, И, К, М, М, Т, Т. Какова вероятность того, что при случайном расположении букв в ряд он получит слово МАТЕМАТИКА?

2.13. Бросаются 4 игральные кости. Найти вероятность того, что на них выпадет по одинаковому числу очков.

2.14. В ящике 10 красных и 6 синих пуговиц. Какова вероятность того, что две наудачу вынутые пуговицы будут одноцветными?

2.15. В урне имеется 5 белых, 6 черных и 4 красных шара. Из урны наугад одновременно извлекают 3 шара. Какова вероятность того, что все шары будут:

а) одного цвета;

б) разных цветов?

2.16. Колода игральных карт (52 листа, 4 масти по 13 карт в каждой) тщательно перетасована. Наудачу берут 6 карт (без возвращения). Найти вероятности того, что среди этих карт

а) окажется король пик;

б) окажутся представители всех мастей;

в) будет ровно 5 карт одной масти.

2.17. Из колоды (52 листа) наудачу вынимаются три карты. Найти вероятности того, что:

а) среди них окажется ровно один туз;

б) среди них окажется хотя бы один туз;

в) это будут тройка, семерка и туз (в любом порядке).

2.18. Колоду карт (36 листов) наудачу разделяют на две равные пачки. Чему равна вероятность, что:

а) в каждой из пачек окажется по два туза;

б) в одной из пачек окажется все четыре туза;

в) в пачках окажется по равному числу красных карт?

2.19. Числа 1, …,nрасположены в случайном порядке. Найти вероятность того, что числа

а) 1 и 2; б) 1, 2 и 3

расположены рядом в указанном порядке.

2.20. На полке в случайном порядке расставленоnкниг, среди которых находится двухтомник Д. Лондона. Предполагая, что различные расположения книг равновероятны, найти вероятность того, что оба тома расположены рядом.

2.21. Цифры 1, 2, 3, 4 и 5 написаны на пяти карточках. Наудачу вынимаются по одной три карточки и кладутся рядом слева направо. Какова вероятность того, что полученное число окажется четным?

2.22. Из цифр 1, 2, 3, 4 и 5 сначала выбирают одна, а затем из оставшихся четырех – вторую. Найти вероятность того, что:

а) в первый раз; б) во второй раз; в) оба раза

будет выбрана нечетная цифра.

2.23. Ящик содержит 90 годных и 10 дефектных шурупов. С какой вероятностью среди десяти наудачу взятых шурупов нет дефектных?

2.24. Найти вероятность того, что:

а) дни рождения 12 человек придутся на 12 разных месяцев года (предполагается, что все месяцы равновероятны);

б) дни рождения 6 человек придутся в точности на два месяца.

2.25. Бросаются 5 игральных костей. Найти вероятность того, что по меньшей мере на

а) двух; б) трех

из них выпадут одинаковые грани.

2.26. В купейный вагон (9 купе по 4 места) семи пассажирам продано семь билетов. Найти вероятность того, что оказались занятыми

а) ровна два купе; б) ровно три купе.