Тема 6. Схема бернулли.

ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ В СХЕМЕ БЕРНУЛЛИ

Если производятся испытания, при которых вероятность появления некоторого события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называются независимыми относительно события А. Наступление события А при испытании часто называют “успехом”, в противном случае говорят о “неудаче”. Вероятности этих исходов обозначают p и q = 1 – p (0 £ p, q £ 1) соответственно. Если независимые испытания проводятся в одних и тех же условиях, то вероятность “успеха” в каждом испытании одна и та же. Описанная выше последовательность независимых испытаний с двумя исходами (“успехом” и “неудачей”) и постоянной вероятностью “успеха” в каждом испытании называется схемой Бернулли.

В схеме Бернулли основной интерес представляет вероятность P_n(k) того, что в n независимых испытаниях будет ровно k “успехов”. Если вероятность “успеха” в каждом испытании равна р, то вероятность P_n(k) определяется формулой Бернулли:

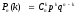(k = 0, 1, …, n; q = 1 – p), (6.1)

где

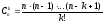–число сочетаний из n по k.

Из формулы Бернулли (6.1) вытекает формула для вероятности P_n(k₁; k₂) того, что в n испытаниях событие А наступит не менее не менее k₁, но не более k₂ раз (от k₁ до k₂ раз):

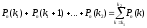P_n(k₁; k₂) = . (6.2)

В качестве частного случая последней формулы получается следующая формула для вероятности того, что в n испытаниях событие А наступит хотя бы один раз:

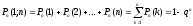, (6.3)

где q = 1 – p.

При большом числе испытаний n вычисление вероятностейP_n(k) иP_n(k₁,k₂) по точным формулам (6.1) и (6.2) становится затруднительным. Поэтому возникает задача замены точных формул приближенными, снижающими вычислительные трудности без значительной потери точности вычислений. Предельные теоремы в схеме Бернулли дают такие формулы для приближенного вычисления вероятностейP_n(k) иP_n(k₁,k₂).

Локальная теорема Муавра – Лапласа. Если число испытаний n в схеме Бернулли достаточно велико, а вероятность “успеха” p не близка ни к 0, ни к 1, так что npq ³ 9, то

P_n(k) »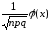, (6.4)

_где и _.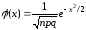

При решении задач, требующих применения локальной теоремы Муавра-Лапласа, пользуются специальными таблицами значений функции j(х). Значения этой функции при хÎ[0; 4] приведены в различных таблицах (см., например, в таблицу 1 Приложения 2 в [1] или таблицу 1.1 в [2]). Для отрицательных значений аргумента x пользуются теми же таблицами, поскольку функция j(х) четная, т.е. j( –х) = j(х). С увеличением значений аргумента x функция j(х) ® 0 , так что при x ³ 4 практически значения функции j(х) » 0.

Интегральная теорема Муавра – Лапласа. Если число испытаний n в схеме Бернулли достаточно велико, а вероятность “успеха” p не близка ни к 0, ни к 1, так что npq ³ 9, то

P_n(k₁; k₂) » Ф₀(x₂) – Ф₀(x₁), (6.5)

где

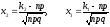и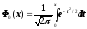- функция Лапласа.

Функция Ф₀(х) табулирована; значения этой функции при хÎ[0; 5] приведены в различных таблицах (см., например, в таблицу 2 Приложения 2 в [1] или таблицу 1.2 в [2]). Для отрицательных значений аргумента x пользуются теми же таблицами, поскольку функция Ф₀(х) нечетная, т.е. Ф₀( –х) = – Ф₀(х). С увеличением аргумента x функция Ф₀(х) ® 0,5 , так что при x ³ 5 практически значения функции Ф₀(х) » 0,5.

Следствие (Вероятность отклонения относительной частоты (доли) от вероятности “успеха”). Пусть n_n – число «успехов» и n_n /n – относительная частота (доля) “успехов” в n независимых испытаниях с постоянной вероятностью p “успеха” в каждом испытании. Если выполнены условия теорем Муавра – Лапласа, то для любого числа e > 0

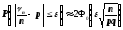, (6.6)

где Ф₀(х) – функция Лапласа.

Теорема Пуассона. Если число испытаний n в схеме Бернулли достаточно велико, а вероятность “успеха” p мала, так что npq £ 9, то для любого фиксированного числа k = 0, 1, …, n

P_n(k) » , (6.7)

где l = np.

Заметим, что в данной ситуации нет теоремы, аналогичной интегральной теореме Муавра-Лапласа. Поэтому для нахождения приближенного значения вероятности P_n(k₁; k₂) необходимо суммировать вероятности P_n(k), определяемые по теореме Пуассона:

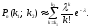(6.8)

Функция P(k; l) = , присутствующая в формулах (6.7) и (6.8), табулирована, её значения приведены в различных таблицах (см., например, в таблицу 3 Приложения 2 в [1] или таблицу 6 в [2]).

Процедура выбора формул для вычисления вероятностей P_n(k) и P_n(k₁, k₂) при различных значениях параметров n и p представлена ниже.

Нет

Нет

СХЕМА БЕРНУЛЛИ:

 n независимых испытаний;

 постоянная вероятность “успеха” p

в каждом испытании (q= 1 –p).

Число

испытаний n

велико?

Нет

Да

Вероятность

“успеха” p

мала?

Нет

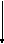
Да

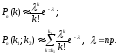
Пример 6.1.По самолету производится три независимых выстрела, причем вероятность попадания при каждом выстреле равна 0,75. Для вывода самолета из строя достаточно трех попаданий; при двух попаданиях он выходит их строя с вероятностью 0,75, а при одном – с вероятностью 0,5. Определить вероятность вывода самолета из строя в результате трех выстрелов.

Решение.Условия примера 6.1 аналогичны условиям примера 5.2, за единственным исключением: вероятность попадания в самолет при всех выстрелах одинакова и равна 0,75. Представим испытание примера 5.2 – три независимых выстрела по самолету – как трехкратное повторение более простого испытания – выстрела по самолету. Тогда получим схему Бернулли сn= 3 независимыми испытаниями и постоянной для всех испытаний вероятностью “успеха” – попадания в самолет – равнойp= 0,75 иq= 1 –p= 0,25.

Да

В обозначениях примера 5.2 имеем

P(A/H₀) = 0;P(A/H₁) = 0,5;P(A/H₂) = 0,75;P(A/H₃) = 1

и

;

;

;

.

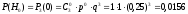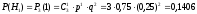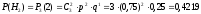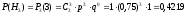Контроль:.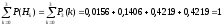

Окончательно по формуле полной вероятности находим

. g

Пример 6.2. По данным проверки расхода электроэнергии за одни сутки в одном из микрорайонов города N установлено, что в среднем в 80% расход электроэнергии не превышает установленной нормы. Какова вероятность того, что в ближайшую неделю расход электроэнергии в данном микрорайоне города N превысит установленную норму в течение: a) трех суток; b) более трех суток; c) менее трех суток; d) хотя бы одних суток?

Решение. Пусть испытание состоит в проверке расхода электроэнергии за одни сутки в рассматриваемом микрорайоне города N. Производится n = 7 таких испытаний, которые являются, очевидно, независимыми: результат проверки в один из каких-либо дней не зависит от результатов проверки в другие дни.

“Успехом” испытания назовем появление события А, состоящего в том, что расход электроэнергии превысит установленную норму. По условию р = Р(А) = 0,2 (q = 1 – p = 0,8) и эта вероятность одинакова при всех испытаниях.

Таким образом, контроль потребления электроэнергии в данном примере описывается схемой Бернулли. Поскольку число испытаний n = 7 невелико, вероятности событий в п.п. a) – d) можно найти с помощью точных формул (6.1) – (6.3):

a) ;

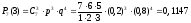b) P₇(4; 7) = P₇(4) + P₇(5) + P₇(6) + P₇(7) =

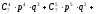
…..…… + ………… + ………… + ………. = 0,033;

c) P₇(0; 2) = …… + …… + …… = ………… + .……… + ………….. =

= ……….. + ..……… + ..…….. = 0,852;

d) P₇(1; 7) = 1 – q⁷ = 1 – (0,8)⁷ » 0,79.

Пример 6.3. В условиях примера 6.2 вычислить вероятность того, что в будущем не високосном году расход электроэнергии в данном микрорайоне города N не превысит установленную норму в течение:

1. 285 суток; b) не менее 285 суток; c) не более 300 суток;

d) не мене 282, но не более 302 суток.

Решение. Рассматриваемое испытание то же самое, что и в примере 6.2, – проверка расхода электроэнергии за одни сутки в интересующем нас микрорайоне города N. “Успехом” же испытания назовем появление события , состоящего в том, что расход электроэнергии не превысит установленную норму. Тогда по условию вероятность “успеха”р = Р() = 0,8 иq = 1 – p = 0,2.

Так как число испытаний n = 365 велико и величина npq = 365×0,8×0,2 = 58,4 > 9, то вероятности событий в п.п. a) – d) вычислим с помощью приближенных формул (6.4) и (6.5):

a)

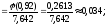
b)

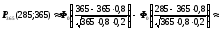
» Ф₀(9,55) –Ф₀(– 0,92) = Ф₀(9,55) +Ф₀(0,92) » 0,5 + 0,321 = 0,821;

c)

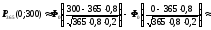
» …………………………. = …………………………. » ……………… = 0,853;

d)

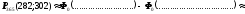
»…………………….. = ….………………….. = …………..»0,81.

При вычислении вероятностей в п.п. a) – d) мы воспользовались свойствами функций j(х) и Ф₀(х), а также таблицами их значений.

Пример 6.4. Изделия, произведенные на заводе, проходят проверку на стандартность в отделе технического контроля (ОТК). Из практики производства изделий данного типа известно, что из 100 изделий в среднем 85 являются стандартными.

1. Какова вероятность того, что среди 200 проверенных в ОТК изделий доля стандартных будет: a) равна 83%; b) не менее 83%; c) не более 90%; d) не менее 80%, но не более 90%?

2. Сколько нужно проверить изделий, чтобы с вероятностью 0,97 можно было утверждать, что доля стандартных изделий среди них отклонится по абсолютной величине от вероятности производства стандартного изделия не более, чем на 0,02?

Решение. Испытанием будем считать проверку качества изделия в ОТК завода, а “успехом” испытания – признание изделия стандартным. По условию количество испытаний n = 200 достаточно велико, а вероятность “успеха” p = 0,85 хотя и близка к единице, но величина npq = 200×0,15×0,85 = 25,5 > 9. Поэтому для решения данной задачи можно использовать формулы (6.4) – (6.6).

1. a) Так как от общего количества n = 200 проверенных в ОТК изделий 83% стандартных составят k = 200×0,83 = 166 изделий, то по локальной теореме Муавра-Лапласа находим

.

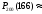
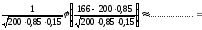
b) Аналогично с помощью интегральной теоремы Муавра-Лапласа получаем

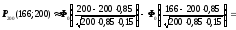
»…………………………. = ……………………»…………………. = 0,785.

c) Поскольку 90% от 200 изделий составляют k₂ = 180 изделий (k₁ = 0), то по интегральной теореме Муавра-Лапласа находим

P₂₀₀(0; 180) » ………………………………………………. »

» ………………………… = …………………… = …………….. = 0,976.

d) I способ (использование интегральной теоремы Муавра-Лапласа).

II способ (применение формулы (5.6) для вероятности отклонения относительной частоты (доли) от вероятности “успеха”).

Очевидно, доля стандартных изделий p = 0,85 составляет в процентах 85%, а 80% – 85% = – 5% и 90% – 85% = 5% составляют в долях – 0,05 и 0,05 соответственно. Тогда, подставляя в формулу (5.6) n = 200, p = 0,85, q = 0,15 и e = 0,05, получаем

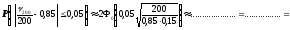
2. Нам нужно определить число испытаний n из равенства

.

Вероятность, фигурирующую в левой части, заменяем, в силу формулы (6.6), её приближенным значением. Для определения n в результате получается приближенное равенство

_, или

По таблице значений функции Лапласа Ф₀(х) находим, что 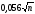» 1,88,

откуда

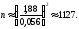
Пример 6.5. В центральный банк города N от коммерческих структур поступило 10 тысяч стодолларовых купюр. Среднее число фальшивых стодолларовых купюр, находящихся в обращении в городе N, составляет 0,05%.

Вычислить вероятность того, что среди поступивших в банк стодолларовых купюр фальшивых будет: a) пять; b) более пяти; c) менее пяти; d) хотя бы одна.

Решение. Пусть испытание состоит в проверке стодолларовой купюры на фальшивость в центральном банке города N, а “успех” испытания – установление ее фальшивости. По условию количество испытаний n = 10 000 велико, а вероятность “успеха” p = 0,0005 мала. Кроме того, величина npq = 10 000×0,0005×0,9995 < 9, и поэтому для решения данной задачи следует использовать теорему Пуассона. Применяя формулы (6.7) и (6.8) с l = np = 10000 × 0,0005 = 5 и таблицу значений функции P(k; l) = 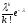, находим:

a) ;

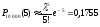b)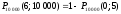

= 0,384;

c)

= ;

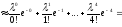
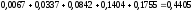d)P_{10 000}(1; 10 000) = 1 –P_{10 000}(0)»1 –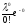= 1 – 0,0067 = 0,9937. g

6.6. В приборе стоят 6 одинаковых предохранителей. Известно, что после 1 000 часов работы прибора выходит из строя в среднем 35% предохранителей данного типа. Если выходит из строя не менее двух предохранителей, то прибор требует ремонта. Определить вероятность того, что прибор не будет нуждаться в ремонте после 1 000 часов работы, если предохранители выходят из строя независимо друг от друга.

6.7. По мишени произведено пять независимых выстрелов в одинаковых условиях, которые дали три попадания. Какое значение вероятности попадания при одном выстреле более вероятно: 1/2 или 2/3, если до выстрелов обе гипотезы были равновероятны?

6.8. Две электрические лампочки включены в цепь параллельно. Вероятность того, что при повышении напряжения в цепи выше номинального перегорит только одна лампочка, равна 0,18. Найти вероятности перегорания каждой из этих лампочек, если известно, что эти вероятности превосходят 0,7 и равны между собой.

6.9. В страховой компании застраховано 500 автомобилей одной марки. Известно, что при аварии крупная поломка автомобилей данной марки происходит в среднем в 15% всех аварий. Каждый владелец застрахованного автомобиля платит компании в год 1 200 рублей страховых и в случае крупной поломки автомобиля в результате аварии получает от компании 50 000 рублей. Найти вероятность того, что по истечении года работы страховая компания:

а) потерпит убытки; b) получит прибыль не менее, чем 200 000 рублей.

6.10. На склад поступает одинаковая продукция с трех предприятий. Продукция 1-го предприятия составляет на складе 25%, 2-го – 35%, а остальная продукция на складе 3-го предприятия. В продукции 1-го предприятия в среднем 65% изделий высшего сорта, в продукции 2-го – 75% и в продукции 3-го – 60%. Определить вероятность того, что среди 300 наудачу взятых на складе изделий не более трети будут изделиями не высшего сорта.

6.11. При изготовлении отливок получается в среднем 20% дефектных. Сколько необходимо запланировать отливок к изготовлению, чтобы с вероятностью не менее 0,95 была обеспечена программа выпуска изделий цехом, для выполнения которой необходимо изготовить не менее 50 бездефектных изделий?

6.12. Известно, что в некоторой лотерее выигрышными являются 0,5% всех билетов. Сколько нужно купить билетов данной лотереи, чтобы вероятность выигрыша хотя бы по одному из них была не меньшей, чем 0,95?

Указание. Решите данную задачу двумя способами: с помощью формулы (6.3) и теоремы Пуассона. Сравните полученные результаты.

6.13. Автомат по продаже прохладительных напитков срабатывает правильно в среднем в 98 случаях из 100. Определить вероятность того, что при 200 попытках автомат сработает правильно не менее 196 раз.

6.14. В течение часа коммутатор, установленный для включения телефонных аппаратов в офисах торговой фирмы, получает в среднем 60 вызовов. Конструкция коммутатора такова, что в течение одной секунды на него может поступить не более одного вызова. Найти вероятность того, что в течение 3 минут, когда коммутатор был неисправен, поступят:

а) не более трех вызовов; b) хотя бы один вызов.