
- •По дисциплине
- •Аннотация
- •Раздел 1. Основные понятия теории вероятностей
- •Тема 1. Пространство элементарных исходов и события.
- •Тема 2. Классическое определение вероятности
- •По определению полагается
- •Тема 3. Геометрическое определение вероятности
- •Тема 4. Теоремы сложения и умножения вероятностей
- •Тема 5. Формулы полной вероятности и байеса
- •Тема 6. Схема бернулли.
- •Тема 7. Дискретные случайные величины
- •Тема 8. Непрерывные случайные величины
Тема 5. Формулы полной вероятности и байеса
Предположим, что в результате испытания событие Аможет произойти вместе с одним из попарно несовместных событийH1,H2, …,Hn, составляющих полную группу. Тогда вероятность событияАможно найти с помощьюформулы полной вероятности
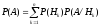 .
.
Поскольку заранее неизвестно, какое из событий H1,H2, …,Hnнаступит в результате испытания, их часто называютгипотезами. Необходимым (но не достаточным) условием того, чтоH1,H2, …,Hnобразуют полную группу попарно несовместных событий, является выполнение равенства:
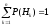 .
.
Пусть до испытания известныаприорные(доопытные) вероятности гипотезР(Н1), Р(Н2), …,Р(Нn). После испытания становится известно, что произошло некоторое событиеА. Каковы теперьапостериорные(послеопытные) вероятности гипотез при условии, что событиеАпроизошло? Ответ даетсяформулой Байеса
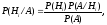 i= 1, 2, ….,n,
i= 1, 2, ….,n,
где вероятность события Аопределяется формулой полной вероятности.
Формула Байеса позволяет переоценить вероятности гипотез после поступления новой информации относительно осуществления того или иного события. Апостериорные вероятности, как и априорные, удовлетворяют соотношению
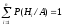 .
.
Пример5.1.В торговую фирму поступили телевизоры от трех поставщиков в отношении 1:2:3. Практика показала, что телевизоры, поступающие от 1-го, 2-го и 3-го поставщиков, не потребуют ремонта в течение гарантийного срока соответственно в 85%, 90% и 95% случаев.
1). Определить вероятность того, что проданный торговой фирмой телевизор не потребует ремонта в течение гарантийного срока.
2). Проданный телевизор потребовал ремонта в течение гарантийного срока. От какого поставщика вероятнее всего поступил этот телевизор?
Решение.Испытание – проверка качества в течение гарантийного срока купленного в торговой фирме телевизора.
1). Пусть событие Асостоит в том, что проданный телевизор не потребует ремонта в течение гарантийного срока. Так как не известно, от какого поставщика проданный телевизор, то введем гипотезы
Нi= {телевизор поступил в торговую фирму отi-го поставщика},i= 1, 2, 3.
По условию
P(A / H1) = 0,85; P(A / H2) = 0,90; P(A / H3) = 0,95.
Согласно классическому определению вероятности, имеем
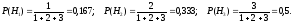
Контроль:P(H1) +P(H2) +P(H3) = 0,167 + 0,333 + 0,5 = 1.
По формуле полной вероятности находим
Р(А) =Р(Н1) ·Р(А/Н1) +Р(Н2) ·Р(А/Н2) +Р(Н3) ·Р(А/Н3) =
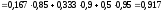 .
.
2). Событие
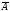 = {телевизор потребует ремонта в течение
гарантийного срока};
= {телевизор потребует ремонта в течение
гарантийного срока};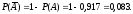
Исходя из условия и свойств условной вероятности, получим
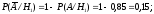
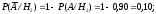
 .
.
По формуле Байеса находим
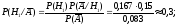
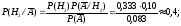
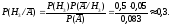
Контроль: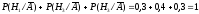 .
.
Таким образом,
после наступления события
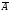 вероятность гипотезыН2увеличилась сР(Н2) = 0,333
до максимальной
вероятность гипотезыН2увеличилась сР(Н2) = 0,333
до максимальной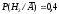 ,
а гипотезыН3– уменьшилась
от максимальной Р(Н3) = 0,5
до минимальной
,
а гипотезыН3– уменьшилась
от максимальной Р(Н3) = 0,5
до минимальной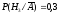 .
Если ранее (до наступления события
.
Если ранее (до наступления события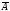 )
наиболее вероятной была гипотезаН3,
то теперь, в свете новой информации
(наступления события
)
наиболее вероятной была гипотезаН3,
то теперь, в свете новой информации
(наступления события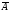 ),
наиболее вероятна гипотезаН2– поступление данного телевизора от
2-го поставщика.g
),
наиболее вероятна гипотезаН2– поступление данного телевизора от
2-го поставщика.g
Пример 5.2.По самолету производится три независимых выстрела, причем вероятность попадания приi-м выстреле равна 0,75 + 0,05i,i= 1, 2, 3. Для вывода самолета из строя достаточно трех попаданий; при двух попаданиях он выходит их строя с вероятностью 0,75, а при одном – с вероятностью 0,5. Определить вероятность вывода самолета из строя в результате трех выстрелов.
Решение.Испытание – по самолету производится три независимых выстрела. Интересующее нас событиеAзаключается в выведении самолета из строя. Поскольку неизвестно количество попаданий в самолет, то выдвигаем 4 гипотезы:
Hk= {в самолет произошлоkпопаданий},k= 0, 1, …, 3.
По условию задачи известны части вероятности событияA(при условияхHk,k= 0, 1, …, 3):
P(A/H0) = 0; P(A/H0) = 0,5; P(A/H0) = 0,75; P(A/H0) = 1.
Полнуювероятность событияAнайдем по формуле полной вероятности, поскольку условия ее применения выполнены: событияH0, … ,H3, очевидно, попарно несовместны и образуют полную группу событий.
Указание. Если выбрать в качестве гипотез события, состоящие в попадании в самолет приk-м выстреле (k= 1, …, 3), то формулу полной вероятности применятьнельзя, так как эти события будут совместными и не будут образовывать полную группу.
Для нахождения вероятностей гипотез введем события
Ai= {приi-м выстреле произошло попадание в самолет},i= 1, 2, 3.
По условию задачи P(A1) = 0,8;P(A2) = 0,85;P(A3) = 0,9. Вероятности гипотезP(Hk),k= 0, 1, …, 3, вычислим с помощью теорем сложения и умножения вероятностей (см. тему 4).
Имеем
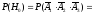 ……………………..
= ……………………………… = 0,003;
……………………..
= ……………………………… = 0,003;
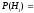 ……………………………………………………………………………………= 0,056;
……………………………………………………………………………………= 0,056;
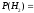 …………………………………………………………………………………….
= ……..;
…………………………………………………………………………………….
= ……..;
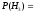 ……………= ………………………..
= ……………………………… = ……. .
……………= ………………………..
= ……………………………… = ……. .
Контроль: …………………………………………………………………
По формуле полной вероятности находим окончательно
Р(А) =Р(Н0) ·Р(А/Н0) +Р(Н1) ·Р(А/Н1) +Р(Н2) ·Р(А/Н2) +Р(Н3) ·Р(А/Н3) =
Пример 5.3.В условиях задачи 5.2 в результате трех выстрелов самолет не был выведен из строя. Какова вероятность того, что не произошло ни одного попадания в самолет?
Решение.
В результате испытания – трех выстрелов
по самолету – становится известно, что
произошло событие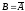 = {самолет не будет выведен из строя}.
Требуется теперь пересчитать априорную
вероятность нулевого числа попаданий
в самолетP(H0)
при этом условии. Для этого можем
воспользоваться формулой Байеса,
поскольку все условия для ее применения
выполнены (см. решение примера 5.2):
= {самолет не будет выведен из строя}.
Требуется теперь пересчитать априорную
вероятность нулевого числа попаданий
в самолетP(H0)
при этом условии. Для этого можем
воспользоваться формулой Байеса,
поскольку все условия для ее применения
выполнены (см. решение примера 5.2):

Пример 5.4.Среди 30 экзаменационных билетов имеется 10 “счастливых”. Студенты поочередно берут по одному билету (без возвращения). У кого больше вероятность взять “счастливый” билет: у того, кто берет билет первым, вторым, третьим и т. д. тридцатым?
Решение. Испытание – студент берет один билет первым или вторым, или третьим, или и т.д. тридцатым. Поскольку речь идет о выполненииразных комплексов условий, то мы имеем 30разных испытаний(см. тему 1). Следовательно, для решения одной задачи надо решить 30 других задач. Пусть событиеА(во всех задачах) состоит в том, что студент возьмет “счастливый” билет.
I). Испытание – студент берет билет первым. Для него вероятность взять “счастливый” билет, очевидно, равна, в силу классического определения,Р(А) = 10/30 = 1/3.
II). Испытание – студент берет билет вторым. Так как до 2-го студента билет берет первый и неизвестно, какой он взял билет, можно выдвинуть две гипотезы:
Н1= {1-й студент взял “счастливый” (для 2-го) билет},
Н2= {1-й студент взял “несчастливый” (для 2-го) билет}.
Очевидно, события Н1иН2несовместны и образуют полную группу. Легко видеть, что по классическому определению вероятности
Р(Н1) = 10/30 = 1/3,Р(Н2) = 20/30 = 2/3.
Контроль: P(H1) + P(H2) = 1/3 + 2/3 = 1.
После того, как 1-й студент взял билет остается 29 билетов, из которых 9 “счастливых” (если выполнено условие Н1) или 10 “счастливых” (если выполнено условие Н2). Классическое определение вероятности дает нам
Р(А/Н1) = 9/29 иР(А/Н2) = 10/29.
Тогда по формуле полной вероятности находим
Р(А) =Р(Н1) ·Р(А/Н1) +Р(Н2) ·Р(А/Н2) =
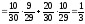 .
.
Таким образом, вероятность взять “счастливый” билет для 2-го студента также равна Р(А) = 1/3.
III). Испытание – студент берет билет третьим. Перед третьим студентом берут билеты два предыдущих. Так как неизвестно, какие билеты они взяли, выдвигаем следующие гипотезы:
Н1= {первые два студента взяли два “счастливых” (для 3-го студента) билета};
Н2= {первые два студента взяли один “счастливый” и один “несчастливый”
(для 3-го студента) билета};
Н3= {первые два студента взяли два “несчастливых” (для 3-го студента) билета}.
Очевидно, события Н1,Н2,Н3попарно несовместны и образуют полную группу.
Для вычисления вероятностей гипотез воспользуемся формулой для гипергеометрических вероятностей (см. тему 2) с n= 30 (все билеты),n1= 10 (все “счастливые” билеты),k= 2 (взятые двумя первыми студентами билеты),k1= 2, 1, 0 (“счастливые” билеты среди взятых); получим тогда

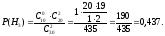
Контроль:P(H1) +P(H2) +P(H3) = 0,103 + 0,460 + 0,437 = 1.
После того, как взяли билеты два первых студента остается 28 билетов, из которых 8 “счастливых” (если выполнено условие Н1), 9 “счастливых” (если выполнено условие Н2) или 10 “счастливых” (если выполнено условие Н3). Классическое определение вероятности дает нам
Р(А/Н1) = 8/28,Р(А/Н2) = 9/28 иР(А/Н3) = 10/28.
По формуле полной вероятности находим тогда
Р(А) =Р(Н1) ·Р(А/Н1) +Р(Н2) ·Р(А/Н2) +Р(Н3) ·Р(А/Н3) =
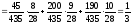 .
.
Таким образом, вероятность взять “счастливый” билет для третьего студента снова равна Р(А) = 1/3.
IV) Испытание – студент берет билет четвертым.
5.5.В 1-й урне содержится 10 шаров, из них 4 белых; во 2-й урне 20 шаров, из них 6 белых. Из каждой урны наугад извлекли по одному шару, а затем из этих двух шаров также наугад взяли один шар. Найти вероятность того, что взят белый шар.
5.6. В коробке 12 теннисных мячей, из которых 9 новых. Для 1-й игры наудачу берутся три мяча, которые после игры возвращаются в коробку. Какова вероятность того, что три мяча, наугад взятые для 2-й игры, будут новыми?
5.7.Пятнадцать экзаменационных билетов содержат по три вопроса, которые не повторяются. Студент может ответить только на 30 вопросов. Определить вероятность того, что экзамен будет сдан студентом, если для этого необходимо ответить не менее чем на два вопроса из одного билета или на один вопрос из одного билета и на указанный дополнительный вопрос из другого билета.
5.8.Производится один выстрел по плоскости, на которой расположены две не пересекающиеся цели. Вероятность попадания в 1-ю цель равна 0,35, во 2-ю – 0,45. После выстрела получено известие, что попадания во 2-ю цель не произошло. Какова вероятность того, что произошло попадание в 1-ю цель?
5.9.У рыбака имеется три любимых места для ловли рыбы, которые он посещает с одинаковой вероятностью каждое. Если он закидывает удочку, то рыба клюет на 1-м месте в среднем в 20% , на 2-м – в 30% и на 3-м – в 35% всех закидываний удочки. Однажды, придя на ловлю рыбы в одно из этих трех мест, рыбак три раза забросил удочку, а рыба клюнула только один раз. На каком месте вероятнее всего рыбачил рыбак?
