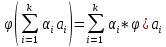• || Базисом в линейном пространстве называется упорядоченная конечная система векторов, если:

  • Она линейно независима

  • Каждый вектор из раскладывается в линейную комбинацию векторов этой системы

• Из одного и того же множества векторов можно составить разные базисы, по-разному нумеруя векторы

• Существует максимальная линейно независимая система , добавление любого вектора из увеличивает число векторов на 1, и они становятся линейно зависимыми, тогда число векторов называется размерностью линейного пространства

  • 

    • || это максимальное число линейно независимых векторов.

  • Самая максимальная линейно независимая система называется базисом

• Теорема о разложении по базису

  • 

  • В конечномерном линейном пространстве с произвольным базисом из векторов любой вектор однозначно разлагается в линейную комбинацию базисных векторов.

    • Добавим к базису произвольный вектор

      • 

      • 

    • Докажем, что в 2

      • Докажем от противного. Пусть (из условия линейной независимости базиса)

Тогда получилось, что система оказалась линейно независимой, что противоречит определению базиса, как линейно независимой системы.

• Тогда

• Доказать от противного единственность разложения

  • 

  • 

    • 

Билет 18. Операции над подпространствами, прямая сумма подпространств.

• Подпространство в пространстве L называется его линейным подпространством если само является пространством с определенными операторами в L.

• 

• 

• будут выполнены в

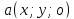
• Прямая сумма

||-прямая сумма. Если обычная сумма y подпространств – нулевое пересечение.

Если подпространства пересекаются по нулевому элементу и имеют сумму размерностей равную размерности их суммы, то любой элемент в прямой сумме разлагается в виде

Билет 19. Евклидовы пространства, неравенство Коши, ортонормированный базис, связь ортогональности и линейной независимости систем векторов.

В формальных линейных пространствах пока отсутствует теория измерения длин и углов.

Введём аксиоматическое понятие линейного пространства.

• || Линейное пространство является евклидовым, если для любой пары элементов определено скалярное произведение

  • А1.

  • A2.

  • A3.

  • A4.

• С помощью А4 назовём длиной вектора

  • Из векторной алгебры:

• Неравенство Коши – Буняковского.

  • Для любых справедливо такое неравенство

• Доказательство

  • 

    • По А2:

  • Вводим

    • По А4:

    • Тогда выражение

Ортогональность и ортогональные системы векторов

• || Система ненулевых векторов евклидового пространства

• Выясним, можно ли линейно независимую систему сделать ортогональной, а ортогональную – нормированной.

  • 

    • Процесс ортогонализации. Смысл процесса

      • Пусть построим

      • Берём из линейно независимой системы

      • Составим соотношение:

      • Для получения коэффициента будем действовать, исходя из условий

        • 

        • 

      • Умножим 1 на векторы

• Подставим 2 в 1

• Установим связь ортогональности системы и её линейной зависимости

  • ТЕОРЕМА. Всякая ортогональная система линейно независима.

    • 

    • 

• Процесс нормировки – каждый вектор поделить на его длину (я не понимаю свои записи, поэтому написала именно так, но это правда!!)

Билет 20. Процесс ортогонализации грамма – Шмидта, ортогональные дополнения и ортогональные суммы.

• || Система ненулевых векторов евклидового пространства

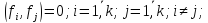
• Выясним, можно ли линейно независимую систему сделать ортогональной, а ортогональную – нормированной.

  • 

    • Процесс ортогонализации. Смысл процесса

      • Пусть построим

      • Берём из линейно независимой системы

      • Составим соотношение:

      • Для получения коэффициента будем действовать, исходя из условий

        • 

        • 

      • Умножим 1 на векторы

• Подставим 2 в 1

• Ортогональные дополнения

Пусть дано произвольное подпространство евклидового пространства.

, тогда назовем множество ортогональным дополнениемподпространства L если для любых скалярное произведение равно 0 (1)

• Теорема 1. Ортогональное дополнение к подпространству L– само подпространство E

все аксиомы от 1 до 8 справедливы.

• Ортогональная сумма

В любом евклидовом пространстве справедливы для подпространства следующие свойства:

• 

усть

• Рассмотрим базисы

Пусть – базис

- базис , базисы ортонормированные

Рассмотрим систему , – ортонормированная

Пусть , не базис . Дополняем эту систему до базиса.

Пусть – дополнительный единичный вектор

,

Из а и б следует, что – базис.

Если объединение базисов подпространств является базисом пространства, то сумма подпространств – прямая сумма = .

Следствие: если Lподпространство евклидового пространства, то всякий элемент xизE можно представить в виде суммы: - единственно.

– проекция вектора xна подпространство L

- ортогональный вектор xна подпространство

Билет 21. Изоморфизм линейных и евклидовых пространств.

• || Два линейных пространства называются изоморфными, если:

  • Между ними существует взаимно однозначное отображение

    • 

    • 

    • 

  • Это отображение сохраняет операции сложения и умножения

    • 

    • 

• Простейшие свойства изоморфизма

  • Линейная комбинация векторов при изоморфизме переходит в линейную комбинацию образов

    • 

  • Образ нуля при изоморфизме даёт ноль.

    • 

    • 

    • 

  • Образ линейно независимой системы при изоморфизме – линейно независимая система

    • 

  • При изоморфизме базис переходит в базис.

    • 

• Критерий изоморфизма линейных пространств

  • Два линейных пространства изоморфны тогда и только тогда, когда имеют одинаковые размерности.

    • Необходимость вытекает из свойств изоморфизма

    • Достаточность

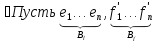
• В силу однозначности разложения по базису ϕ – взаимно однозначны.

• (писать если спросит… я хз) Сохранение операций следует из правил действия над векторами в координатах.

• Понятие изоморфизма линейного пространства

|| Два евклидовых пространства называются изоморфными, если

• Они изоморфны, как линейные, то есть