Симплексный метод решения задач линейного программирования

Симплексный метод применим к решению любой задачи линейного программирования. Из геометрического смысла задачи линейного программирования следует, что для ее решения необходимо вычислить координаты всех вершин многогранника ограничений и значения линейной формы в них. Решить ЗЛП можно методом перебора. Действительно, перебором всех вершин можно найти такую вершину, где функция L приобретает экстремальное значение. При этом возможны две трудности:

1. так как при n > m система ограничений линейно зависима, то для построения многоугольника решений необходимо выделение всех линейно независимых систем уравнений и их решение;

2. число вершин многогранника резко возрастает с увеличением n > m, и такой метод перебора всех вершин может оказаться слишком трудоемким (n - число неизвестных, m - число ограничений).

Симплексный метод обеспечивает более рациональное решение задачи, чем метод перебора. Его существо состоит в том, что, отправляясь из некоторой произвольной вершины многогранника ограничений, переходят к вычислению только такой вершины, в которой значение линейной формы будет больше, чем в предыдущей. Остальные варианты не вычисляются. Тогда при конечном сравнительно малом числе шагов может быть найден оптимальный план. Таким образом, производится упорядоченный перебор вершин, при котором происходит постоянное увеличение линейной формы. Поэтому симплексный метод называется также методом последовательного улучшения плана.

Решение задачи симплексным методом включает в себя два этапа. Первый состоит в нахождении одной произвольной вершины многогранника ограничений, координаты которого определяют начальный опорный план . Второй этап состоит в последовательном упорядоченном переходе от одной вершины многогранника к другой, смежной данной. Так как прилегающих вершин много, то каждый раз выбирается такая вершина, при переходе к которой обеспечивается наибольшее возрастание линейной формы. На каждом шаге процесса улучшения плана производится проверка на оптимальность. Очевидно, что план будет оптимальным, если среди вершин, прилегающих к данной, нет такой, при переходе к которой происходит возрастание линейной формы.

Определение исходного базисного решения

При выборе исходного базисного решения рассматриваемым здесь способом следует различать три случая.

1. Система ограничений задана в виде неравенств, т.е.

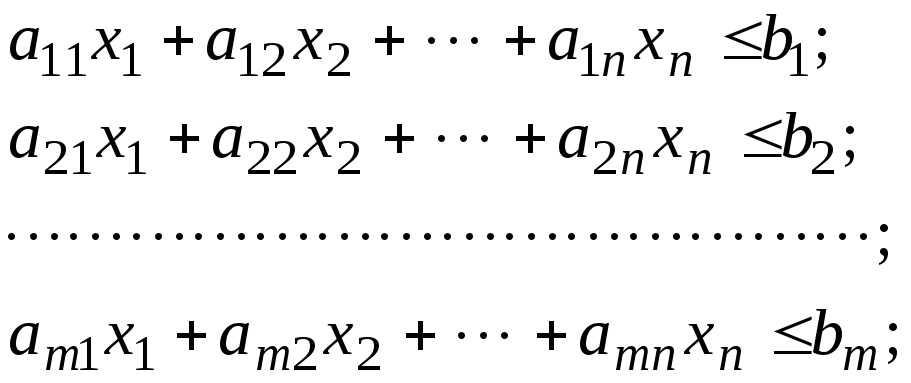(1)

Чтобы перейти от неравенств к равенствам, введем дополнительные неизвестные х_n+1, x_n+2, ¼ x_n+m, которые в линейную форму задачи входят с нулевыми коэффициентами, а в систему ограничений - с коэффициентами, равными единице. Тогда система (1) примет следующий вид:

(2)

Для удобства дальнейших рассуждений запишем коэффициенты системы при одинаковых неизвестных (по столбцам) в виде следующих векторов:

Система ограничений в векторной форме принимает вид

(3)

Векторы являются m-мерными, а их число равно n+m, но так как n + m> m, то они линейно зависимы.

Координаты одной из вершин многогранника ограничений могут быть образованы системой из m линейно независимых векторов. Такую систему называют базисом задачи. Известно, что для нахождения базиса необходимо выделить ту часть системы (2), для которой определитель матрицы, составленной из коэффициентов системы, отличен от нуля. В системе (2) это выполняется для матрицы коэффициентов при дополнительных неизвестных, которая является единичной и ее определитель не равен нулю:

Следовательно, векторы линейно независимы. Координаты вершины, которую образует данный базис, легко получить, приняв и разрешив выделенную из систем (2) систему линейных независимых уравнений:

Следовательно, начальный опорный план есть

Таким образом, путем введения дополнительных неизвестных мы находим координаты начальной вершины, т.е. освобождаемся от необходимости отыскивать системы линейно независимых векторов среди множества и решать системы уравнений для них.

Очевидно, что расширение задачи за счет дополнительных неизвестных увеличивает число вершин многогранника ограничений и число шагов в процессе последовательного упорядоченного перебора вершин в направлении возрастания линейной формы. Это обстоятельство ведет к увеличению времени решения второго этапа, но выигрыш на первом этапе компенсирует его.

2. Система ограничений задана в виде равенств.

В этом случае введение дополнительных неизвестных невозможно, а значит, невозможен и рассмотренный выше простой способ построения начального опорного плана. В то же время отыскание среди n векторов m неизвестных для формирования из них начального базиса по своей трудоемкости ничуть не легче этапа последовательного улучшения плана.

Введем в систему ограничений неизвестные х_n+1, x_n+2, ¼ , x_n+m, которые, в отличие от дополнительных неизвестных, рассмотренных для первого случая, назовем искусственными неизвестными. В линейную форму искусственные неизвестные введем не с нулевыми коэффициентами, а с большим отрицательным коэффициентом М, чтобы в ходе решения обеспечить исключение из плана искусственных переменных. Таким образом, задача в данном случае сводится к максимизации

L^¢ = c₁x₁ + c₂x₂ + ¼ + c_nx_n - M(x_n+1 + x_n+2 + ¼ + x_n+m)

при ограничениях вида (2).

3. Система ограничений задана в смешанной форме, т.е. частью неравенств и частью равенств.

В этом случае для получения исходного базисного решения следует соответственно ввести дополнительные и искусственные неизвестные по правилам, указанным в пп. 1 и 2.

Заметим, что коэффициенты b_i в системе ограничений (2) по смыслу задачи не могут быть отрицательными. Поэтому, если в некотором из ограничений при формальных преобразованиях получено значение b_i < 0, то данное ограничение умножается на -1.

Рассмотрим процедуру получения исходного базисного решения на примере.

Пусть требуется минимизировать линейную форму

L = -5x₁ - 2x₂ - 3x₃ - x₄ + 3x₅ - 6x₆ = min

при ограничениях:

x₁ + 3x₂ + x₃ + x₄ + 6x₅ + 8x₆ = 10;

4x₂ - 2x₃ - 6x₄ - x₅ = -9;

x₂ + 3x₃ + x₅ + x₆ ³ 12

2x₂ - 4x₄ + x₅ + x₆ £ 4

Как указывалось выше, задача минимизации линейной формы соответствует задаче максимизации, если знаки коэффициентов с_i поменять на обратные, т.е.

L^¢ = 5x₁ + 2x₂ + 3x₃ + x₄ - 3x₅ + 6x₆ = max.

Во втором ограничении необходимо сменить знаки на обратные, чтобы получить b₂ > 0, т.е. 4x₂ + 2x₃ + 6x₄ + x₅ = 9.

В третьем ограничении для смены знака неравенства требуется ввести со знаком минус дополнительную неизвестную x₇, т.е. x₂ + 3x₃ + x₅ + x₆ - x₇ = 12, которая войдет в линейную формулу с коэффициентом c₇ = 0.

Так как в системе ограничений один единичный вектор есть, то для получения исходного базисного решения достаточно ввести две искусственные переменные x₈ и x₉ и дополнительную переменную x₁₀. Тогда основная задача линейного программирования для рассматриваемого примера может быть сформулирована следующим образом.

Максимизировать линейную форму

L = 5x₁ + 2x₂ +3x₃ + x₄ - 3x₅ + 6x₆ - M(x₈ + x₉) (4)

при ограничениях:

x₁ + 3x₂ + x₃ + x₄ + 6x₅ + 8x₆ = 10;

4x₂ + 2x₃ + 6x₄ + x₅ + x₈ = 9; x₂ + 3x₃ + x₅ + x₆ - x₇ + x₉ = 12; (5)

2x₂ - 4x₄ + x₅ + x₆ + x₁₀ = 4,

где .

Первый этап обычно выполняется вручную и на его основе для решения задачи на ЭВМ в качестве исходных данных задаются:

1. Общее число неизвестных n (основных, дополнительных и искусственных) и число ограничений m.

2. Вектор коэффициентов линейной формы .

3. Вектор , составляющими которого являются номера базисных переменных. Так как начальный план для рассматриваемого примера включает векторы , то начальное значение равно .

4. Матрица коэффициентов системы ограничений, в которой столбец используется для записи значений базисных переменных .

Для примера (4), (5) матрица коэффициентов равна

.

5. Вектор , сформированный путем выбора из вектора элементов, соответствующих векторам начального базиса

Исходные данные в полном объеме приведены в симплексной табл. 5.

Таблица 5

М=100		ci	0	5	2	3	1	-3	6	0	-100	-100	0
hi	ci	ii i	0	1	2	3	4	5	6	7	8	9	10	Ti
1	5	1	10	1	3	1	1	6	8	0	0	0	0	10
8	-100	2	9	0	4	2	6	1	0	0	1	0	0	1,5
9	-100	3	12	0	1	3	0	1	1	-1	0	1	0	100
10	0	4	4	0	2	0	-4	1	1	0	0	0	1	-1
		di	-2050	0	-487	-498	-596	-167	-66	100	0	0	0

r = 2; k = 4; a_rk = 6; h_r = 8.

Алгоритм симплексного метода

Вычислительный процесс по нахождению оптимального плана имеет итерационный характер. Каждая итерация состоит из двух этапов.

Первый этап заключается в исследовании базисного решения на оптимальность. Если рассматриваемый план удовлетворяет условиям оптимальности, то задача решена, в противном случае переходят ко второму этапу.

На втором этапе определяются вектор , который должен быть введен в базис, и вектор , который должен быть исключен из него, т.е. получается новый базисный план с большим значением линейной формы.

Чтобы найти векторы и , замена которых обеспечивает наибольшее возрастание линейной формы, выразим все векторы, не входящие в базис, через базисные векторы

(6)

где a_ij - проекции вектора на вектор . Запишем систему ограничений (7) в векторной форме в следующем виде:

(7)

Так как то

(8)

Выражение (8) дает решение только в том случае, когда коэффициенты при векторах и нового базиса будут неотрицательными, т.е.

и (9)

Соответствующее новое значение линейной формы примет вид

(10)

Обозначим

(11)

Тогда значение линейной формы в новой вершине многогранника решений можно найти из выражения

(12)

Величину d_j называют оценкой плана. В симплексном методе параметры d_j играют важную роль: их знаки позволяют определить, является ли опорный план оптимальным.

Если d_j ³ 0 для всех j, то данный опорный план является оптимальным, так как на основании (3.22) и ввиду q ³ 0 переход к любой новой вершине ведет к убыванию линейной формы.

Если опорный план неоптимальный, то возможны два случая:

1. Имеется хотя бы один индекс j = k, для которого d_k < 0 и все соответствующие компоненты В этом случае линейная форма не ограничена сверху и задача неразрешима.

2. Для некоторых j d_j < 0 и для каждого такого j, по крайней мере, одна из проекций a_ij >0.

Тогда при переходе к следующей вершине линейная форма согласно (12) возрастает и план улучшается.

Для наиболее быстрого возрастания L необходимо в базис включить тот вектор , для которого оценка d_k < 0 и максимальна по модулю, а вектор , для которого значение положительно и минимально, исключить.

Собственно алгоритм симплексного метода состоит из следующих этапов:

1. Вычислить элементы строки оценки плана .

2. Найти номер k вектора , имеющего максимальную по абсолютной величине отрицательную оценку плана. Если все оценки плана положительны, то план оптимален и следует перейти к п.5.

Вычислить столбец значений q в виде элементов матрицы

3. Найти строку с номером r, где для всех .

Если такой строки нет, то перейти к п. 6.

4. Заменить в векторе номер r на k, а в векторе значение на .

Преобразовать матрицу по следующим формулам:

• элементы столбца с номером k

• элементы строки с номером r

• остальные элементы матрицы (i ¹ r, j ¹ k)

.

Перейти к п.1, т.е. к следующей итерации.

5. Выдать на печать оптимальный план:

• вектор - номера переменных х_i, входящих в оптимальное решение;

• столбец - значения переменных х_i;

• значение линейной формы L = d[0].

5. Выдать на печать информацию о неразрешимости задачи, если d_k < 0.

По этому алгоритму нетрудно написать программы на ЭВМ на языках Паскаль, СИ++ и др.

Последовательность вычислений по описанному алгоритму можно проследить по симплексным табл.3.5 и 3.6. Решение задачи приведено в табл.3.7.

В результате получено оптимальное решение задачи (4), (5):

х₁ = 5,83; х₂ = 0; х₃ = 4; х₄ = 0,17; х₅ = 0;

х₆ = 0; х₇ = 0; х₈ = 0; х₉ = 0; х₁₀ = 4,67, (13)

которое дает максимальное значение линейной форме L = d[0] = 41,3.

Таблица 6

hi	ci	i	Значение j											Ti
			0	1	2	3	4	5	6	7	8	9	10
1 4 9 10	5 1 -100 0	1 2 3 4	8,5 1,5 12 10	1 0 0 0	2,37 0,67 1 4,67	0,67 0,33 3 1,33	0 1 0 0	5,83 0,17 1 1,67	8 0 1 1	0 0 -1 0	-0,17 0,17 0 0,67	0 0 1 0	0 0 0 1	12,7 4,5 4 7,5
		di	-1156	0	-89,7	-299	0	-67,7	-66	100	99,3	0	0

Таблица 7

hi	ci	i	Значение j											Ti
			0	1	2	3	4	5	6	7	8	9	10
1 4 3 10	5 1 3 0	1 2 3 4	5,83 0,17 4 4,67	1 0 0 0	2,11 0,55 0,33 4,2	0 0 1 0	0 1 0 0	5,61 0,05 0,33 1,22	7,78 -0,11 0,33 0,56	0,22 0,11 -0,33 0,44	-0,17 0,17 0 0,67	-0,22 -0,11 0,33 -0,44	0 0 0 1
		di	41,3	0	10,1	0	0	32,1	33,7	0,22	99,3	99,7	0

Заметим, что в оптимальное решение входит дополнительная переменная х_10.. Это свидетельствует о том, что в точке (13) четвертое ограничение системы (5) выполняется как неравенство, так как х₁₀ = 4,67, а остальные три ограничения выполняются как равенства.