
Факультатив
.pdfI. Элементарные финансовые расчеты
1.Основы теории процентов
2.Поток платежей, рента
3.Простейшие кредитные расчеты II. Основы финансового анализа
4.Элементы анализа инвестиционных процессов
I. ЭЛЕМЕНТАРНЫЕ ФИНАНСОВЫЕ РАСЧЕТЫ
1.ОСНОВЫ ТЕОРИИ ПРОЦЕНТОВ
1.1.Рассмотрим некоторую денежную сумму S, которую планируют вложить, например в банк. Обозначим символом P ставку про-
цента, получаемую с вложенной суммы за промежуток времени T, считаемый единичным. При вычислении простых процентов по
ставке P исходная сумма S, по окончании промежутка времени T,
возрастет на долю p, где p = P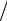 100, от начального значения S, т. е. на
100, от начального значения S, т. е. на
величину pS, и станет равной
S1 = S + pS = S(1+ p) > S .
К концу второго промежутка времени полученная сумма S1 также увеличится долю p от исходного значения S, т. е. на pS, и станет
S2 = S1 + pS = S(1+ p) + pS = S(1+ 2 p) > S1.
Используя метод математической индукции можно легко показать, что в результате начисления процентов в течение N промежутков времени окончательная сумма – наращенная сумма – возрастет и будет равна
SN = S(1+ Np). |
(1.1) |
Полученные формулы показывают, что последовательность наращенных сумм S, S1,Κ SN образует арифметическую прогрессию с начальным членом S и шагом pS.
Пример 1.1. Допустим, дана сумма S = 500 и процентная ставка P = 20%. Тогда суммы, наращенные по схеме простых процентов: 500, 500 + 0,2 500 = 500 + 100 = 600, 600 + 100 = 700, 700 + 100 = 800, и
т. д.♥

Пример 1.2. Годовая ставка простых процентов равна 10%. Через сколько лет начальная сумма удвоится? Составим соотношение S(1+ Np) ≥ 2S . Следовательно, N ≥ 1 p = 1 0,1 = 10 лет.♥
Приведенные формулы наращения простых процентов, рассмотрены для полных интервалов T, т. е. для целых N. Так как зависимость наращения простых процентов от времени (количества временны′х интервалов) описывается линейной функцией, то формула для вычисления, когда рассматривается часть 0 ≤ τ ≤ 1 временно′го интервала T, имеет вид
S′ = S(1+ (N + τ)p), |
(1.2) |
где N – число полных учитываемых временны′х интервалов.
Пример 1.3. При годовой простой процентной ставке P = 10% найти сумму, возвращаемую через два года и три месяца. В этом слу-
чае τ = 3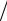 12 = 0,25 и следует выплатить S′= S(1+2,25 0,1) =1,225S .♥
12 = 0,25 и следует выплатить S′= S(1+2,25 0,1) =1,225S .♥
Разность между наращенной и начальной суммами называется процентными деньгами. При работе с простыми процентами процентные деньги растут в арифметической прогрессии, линейно.
1.2. Помимо простых процентов часто используют так называемые сложные проценты. При вычислении сложных процентов по ставке P, сумма S′, начисляемая по окончании промежутка времени
T, возрастет на долю p от суммы S в начале промежутка времени (от предыдущего значения S), т. е. величину pS, и станет равной
S′ = S + pS = S(1+ p) > S ,
где p = P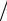 100.
100.
Так, если в начальный момент дана сумма S, то к концу первого промежутка времени будет начислена сумма S1,
S1 = S + pS = S(1+ p),
к концу – второго сумма S2,
S2 = S1 + pS1 = S(1+ p) + pS(1+ p) = S(1+ p)2,
и т. д. Применяя метод математической индукции можно получить, что после завершения N промежутков времени наращенная сумма будет равна
SN = S(1+ p)N . |
(1.3) |

Эта формула показывает, что последовательность S, S1,Κ SN наращенных сумм является геометрической прогрессией с начальным членом S и знаменателем (1+ p).
Пример 1.4. Допустим, дана сумма S = 500 и процентная ставка P = 20%. Тогда суммы, наращенные по схеме сложных процентов,
есть |
500, |
500 +0,2 500 =500 +100 = 600, |
600 +0,2 600 = 720, |
720 +0,2 720 =864, и т. д.♥
Пример 1.5. Годовая ставка сложных процентов равна 12,25%. Через сколько лет начальная сумма удвоится? Составим соотношение S(1+ p)N ≥ 2S . Используя натуральный логарифм, имеем
N ln(1+ p) ≥ ln 2. Поэтому N ≥ ln 2 / ln(1+ p) = ln 2 / ln11225, = 6 лет.♥
Приведенная формула наращения сложных процентов, используется для полных интервалов T, т. е. для целых N. Однако эту формулу можно также применять для неполных интервалов, когда рассматривается часть 0 ≤ τ ≤ 1 временно′го интервала T ,
S′ = S(1+ p)N +τ , |
(1.4) |
где N – число полных учитываемых временны′х интервалов.
Пример 1.6. 2 января в банк положили сумму 5000 до востребования под ставку 11% годовых сложных процентов. Какую сумму получит вкладчик, снимая деньги а) 3 июня текущего года и б) 3 марта следующего года. Для определения требуемых сумм необходимо вычислить τ, а для вычисления τ следует определить количество n дней неполного года, относящегося к периоду выплаты. С хорошей точностью можно считать, что год состоит из 360 дней, а месяц – из
30. Тогда nа = 5 30 и |
nб = 2 30, |
τа = nа 360 = 5 12 = 0,416(6) |
и |
τб = nб 360 = 1 6 = 0,16(6). |
Поэтому |
Sа′ = 5000 (1+ 0,11)5 12 = 5222 |
и |
Sб′ = 5000 (1+ 0,11)1+1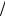 6 = 5647. При необходимости требуемое количество дней можно вычислить точно.♥
6 = 5647. При необходимости требуемое количество дней можно вычислить точно.♥
Также полезно рассмотреть ситуацию, когда по ставке P сложных годовых процентов начисления производятся n раз за год в течение N лет. Это означает, что процентная ставка за период N n равна P
n равна P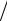 n и всего за N лет проценты начисляются nN раз. Тогда из (1.3) следует
n и всего за N лет проценты начисляются nN раз. Тогда из (1.3) следует
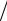
S |
N |
= S 1+ p n |
nN . |
(1.5) |
|
|
a |
f |
|
|
|
Пример 1.7. В силу опредленных обстоятельств на сумму в 1000 начисляются 12 сложных годовых процентов в течение 3-х лет. Чему будет равна наращенная сумма SN? Имеем, n = 12, N = 3 и SN =
= 1000(1+ 0,12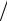 12)36 = 1430,77. Если начислять проценты, как обычно,
12)36 = 1430,77. Если начислять проценты, как обычно,
один раз в год, то n = 1 и SN = 1000(1+ 0,12)3 = 1404,93.♥
При малых вкладах S удвоение капитала по годовой процентной вставке P при наращении сложных процентов приближенно происходит за 72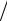 P года. Например, при ставке 4% удвоение капитала ожидается примерно через 72
P года. Например, при ставке 4% удвоение капитала ожидается примерно через 72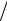 4 = 18 лет.
4 = 18 лет.
Из очевидных неравенств
при N > 1, (1+ p)N > (1+ Np), при τ < 1, (1+ p)τ < (1+ τp),
следует (см. рис. 1.1), если при заданной процентной ставке P период t хранения вклада больше единичного T (N > 1), то по схеме сложных процентов наращение процентов идет быстрее, чем по схеме простых процентов, и наоборот, если период t хранения вклада меньше единичного T (τ < 1).
1.3. Для упрощения и ускорения расчетов составляют таблицы мультиплицирующих и дисконтирующих множителей. Мультиплицирующий множитель M(N, P) показывает, во сколько раз возрастает сумма S, положенная в банк под P сложных годовых процентов
(см. табл. 1.1),
M(N, P) = (1+ p)N , |
(1.6) |
где N – продолжительность хранения вклада и p = P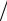 100.
100.
Заметим, что таблица 1.1 и все аналогичные таблицы, приведенные далее, легко могут быть рассчитаны на персональном компьютере, например при помощи табличного процессора Excel, входящего в
MS Office.
Таблица 1.1. Мультиплицирующие множители M(N, P)
N \ P |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
1 |
1,020 |
1,030 |
1,040 |
1,050 |
1,060 |
1,070 |
1,080 |
1,090 |
1,100 |
1,110 |
1,120 |
2 |
1,040 |
1,061 |
1,082 |
1,103 |
1,124 |
1,145 |
1,166 |
1,188 |
1,210 |
1,232 |
1,254 |
3 |
1,061 |
1,093 |
1,125 |
1,158 |
1,191 |
1,225 |
1,260 |
1,295 |
1,331 |
1,368 |
1,405 |

4 |
1,082 |
1,126 |
1,170 |
1,216 |
1,262 |
1,311 |
1,360 |
1,412 |
1,464 |
1,518 |
1,574 |
5 |
1,104 |
1,159 |
1,217 |
1,276 |
1,338 |
1,403 |
1,469 |
1,539 |
1,611 |
1,685 |
1,762 |
6 |
1,126 |
1,194 |
1,265 |
1,340 |
1,419 |
1,501 |
1,587 |
1,677 |
1,772 |
1,870 |
1,974 |
7 |
1,149 |
1,230 |
1,316 |
1,407 |
1,504 |
1,606 |
1,714 |
1,828 |
1,949 |
2,076 |
2,211 |
8 |
1,172 |
1,267 |
1,369 |
1,477 |
1,594 |
1,718 |
1,851 |
1,993 |
2,144 |
2,305 |
2,476 |
9 |
1,195 |
1,305 |
1,423 |
1,551 |
1,689 |
1,838 |
1,999 |
2,172 |
2,358 |
2,558 |
2,773 |
10 |
1,219 |
1,344 |
1,480 |
1,629 |
1,791 |
1,967 |
2,159 |
2,367 |
2,594 |
2,839 |
3,106 |
Таким образом, из (1.3) и (1.6) имеем |
|
SN = S M(N, P), |
(1.3а) |
т. е. величина M(N, P) показывает, какова будет стоимость денежной единицы через N лет при ставке сложного процента P.
Аналогично, если начисления делаются n раз за год по ставке P сложных годовых процентов, то из (1.5) и (1.6) следует
SN = S M(nN, P n). |
(1.5а) |
Дисконтирующий множитель D(N, P) |
показывает долю, кото- |
рую составит начальная сумма S, положенная в банк под P процентов годовых, от наращенной суммы SN к концу N-го года (см. табл. 1.2),
D(N, P) = 1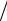 M(N, P) = (1+ p)− N , (1.7)
M(N, P) = (1+ p)− N , (1.7)
где p = P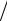 100.
100.
Таблица 1.2. Дискониирующие множители D(N, P)
N \ P |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
1 |
0,980 |
0,971 |
0,962 |
0,952 |
0,943 |
0,935 |
0,926 |
0,917 |
0,909 |
0,901 |
0,893 |
2 |
0,961 |
0,943 |
0,925 |
0,907 |
0,890 |
0,873 |
0,857 |
0,842 |
0,826 |
0,812 |
0,797 |
3 |
0,942 |
0,915 |
0,889 |
0,864 |
0,840 |
0,816 |
0,794 |
0,772 |
0,751 |
0,731 |
0,712 |
4 |
0,924 |
0,888 |
0,855 |
0,823 |
0,792 |
0,763 |
0,735 |
0,708 |
0,683 |
0,659 |
0,636 |
5 |
0,906 |
0,863 |
0,822 |
0,784 |
0,747 |
0,713 |
0,681 |
0,650 |
0,621 |
0,593 |
0,567 |
6 |
0,888 |
0,837 |
0,790 |
0,746 |
0,705 |
0,666 |
0,630 |
0,596 |
0,564 |
0,535 |
0,507 |
7 |
0,871 |
0,813 |
0,760 |
0,711 |
0,665 |
0,623 |
0,583 |
0,547 |
0,513 |
0,482 |
0,452 |
8 |
0,853 |
0,789 |
0,731 |
0,677 |
0,627 |
0,582 |
0,540 |
0,502 |
0,467 |
0,434 |
0,404 |
9 |
0,837 |
0,766 |
0,703 |
0,645 |
0,592 |
0,544 |
0,500 |
0,460 |
0,424 |
0,391 |
0,361 |
10 |
0,820 |
0,744 |
0,676 |
0,614 |
0,558 |
0,508 |
0,463 |
0,422 |
0,386 |
0,352 |
0,322 |
Величину D(N, P) также называют приведенной или современной стоимостью одной денежной единицы, соответствующей периоду N лет при ставке сложного процента P.
1.4. Операция, связанная с выдачей кредита и одновременным удержанием с клиента соответствующих процентов непосредственно в момент выдачи кредита, называется удержанием процентов. Так банк, выдавая кредит S, может взять с клиента соответствующий
процент pS непосредственно в момент выдачи кредита. Тогда клиент получит на руки сумму равную S(1− p), но должен будет вернуть сумму S. Доход банка от этой операции равен Sp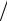 S(1− p) > p. Поэто-
S(1− p) > p. Поэто-
му оказывается, что при удержании процентов банк получает больше декларируемых p процентов.
Пример 1.8. Пусть кредит в 5000 выдается на год под 15% годовых. С клиента в момент выдачи ему кредита удерживают 750, так что на руки он получает 4250. Доход банка определяется отношением 750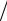 4250 0,1765 и таким образом составляет примерно 17,65%.♥
4250 0,1765 и таким образом составляет примерно 17,65%.♥
Удержание процентов может производиться по схеме простых и сложных процентов. Пусть p – доля (ставка) удержания процентов за каждый единичный (например, годовой) интервал времени T. При использовании схемы удержания простых процентов с суммы кредита S за каждый единичный интервал T удерживается одна и та же величина pS. Поэтому за весь период кредитования удерживается сумма NpS (см. (1.1)–(1.2)). Таким образом, после удержания простых процентов клиент получит в качестве кредита окончательную сумму
SN = S − NpS = S(1− Np). |
(1.8) |
При удержании по схеме сложных процентов за каждый единичный интервал T удерживается доля pS′ от предыдущей суммы S′: при выдаче кредита S на срок T будет удержана сумма pS , а на руки выдана сумма S(1− p); при выдаче кредита на срок 2T удерживается сумма
pS(1− p), а выдается – S(1− p)2; и т. д. Следовательно, при получении на срок NT кредита на сумму S на руки реально будет выдано
SN = S(1− p)N . |
(1.9) |
Формулы (1.8)–(1.9) показывают, что выданные на руки суммы в зависимости от срока кредитования являются убывающей арифметической или геометрической прогрессией. При прочих равных условиях и длительности кредита больше T в случае удержания сложных процентов на руки выдается большая сумма, чем при удержании простых процентов.
Пример 1.9. При получении кредита на сумму 1000 со ставкой удержания 10% при различной длительности кредита на руки будут выданы суммы, указанные в табл. 1.3.♥
Таблица 1.3. Суммы, выдаваемые при получении кредита в 1000
Длительность |
1 |
2 |
3 |
4 |
5 |
Кредита |
|
|
|
|
|
при удержании |
900 |
800 |
700 |
600 |
500 |
простых процентов |
|
|
|
|
|
при удержании |
900 |
810 |
729 |
656,1 |
590,49 |
сложных процентов |
|
|
|
|
|
1.5. Для упрощения и ускорения расчетов при удержании сложных процентов составляют таблицу дисконтных множителей (табл. 1.4). Дисконтный множитель определяет, во сколько раз при удержании сложных процентов по ставке P уменьшится сумма кредита, взятого на период NT,
Dis(N, P) = (1− p)N , |
(1.10) |
где p = P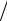 100.
100.
Таблица 1.4. Дисконтные множители Dis(N, P)
N \ P |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
1 |
0.980 |
0.970 |
0.960 |
0.950 |
0.940 |
0.930 |
0.920 |
0.910 |
0.900 |
0.890 |
2 |
0.960 |
0.941 |
0.922 |
0.903 |
0.884 |
0.865 |
0.846 |
0.828 |
0.810 |
0.792 |
3 |
0.941 |
0.913 |
0.885 |
0.857 |
0.831 |
0.804 |
0.779 |
0.754 |
0.729 |
0.705 |
Дисконтный множитель имеет простой экономический смысл, он показывает во сколько раз уменьшается одна денежная единица при удержании с нее сложных процентов по ставке P в течение N периодов. Удержание процентов обычно применяется не более, чем для нескольких интервалов, N ≤ 3.
1.6. Процентная ставка, указываемая в официальных документах, называется номинальной, а ставка, которая получается в реальных расчетах, называется эффективной.
Пусть номинальная годовая ставка P. Если эту ставку начислять n раз в год по схеме сложных процентов по ставке P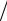 n, то начисленная за год сумма находится по формуле (см. (1.3))
n, то начисленная за год сумма находится по формуле (см. (1.3))
|
|
F |
|
|
pI n |
|
|
||
S = S 1 |
+ |
|
|
|
. |
|
|||
|
nK |
|
|||||||
1 |
|
H |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
Так как эффективная годовая ставка r удовлетворяет соотноше- |
|||||||||
нию S1 = S + rS , то |
|
pI n |
|
|
|
|
|
||
F |
|
|
|
|
|
|
|||
r = H1 |
+ |
|
K |
|
− 1 > p. |
(1.11) |
|||
n |
|
||||||||

Эффективная годовая ставка r определяет коэффициент наращения, который также называют мультиплицирующим множителем
M(n, P n). При частых начислениях, |
точнее при n → ∞ , мультипли- |
||
цирующий множитель M(n, P n) стремится к пределу, |
|
||
lim |
M(n, P n) = lim (1+ p n)n − 1 = ep. |
(1.12) |
|
n→∞ |
n→∞c |
h |
|
где p = P 100. |
|
|
|
Непрерывным наращением по ставке P за единичный промежу-
ток T называется увеличение суммы вклада в ep раз. В общем случае, непрерывное наращение в течение k интервалов времени по ставке P
за промежуток T, приводит к увеличению суммы вклада в ekp раз.
Непрерывным дисконтированием называется уменьшение суммы в
ep раз за промежуток T и уменьшение в ekp раз k промежутков времени.
Если инфляция составляет A процентов в год (a = A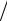 100), то одна и та же группа товаров стоит в конце года в (1+ a) раз больше, чем в его начале. Другими словами, в (1+ a) раз уменьшилась покупательная способность денежной единицы и, следовательно, в столько же раз уменьшилась эффективная процентная ставка. Следовательно, к концу года реальная покупательная способность денежной единицы будет равна (1+ p)
100), то одна и та же группа товаров стоит в конце года в (1+ a) раз больше, чем в его начале. Другими словами, в (1+ a) раз уменьшилась покупательная способность денежной единицы и, следовательно, в столько же раз уменьшилась эффективная процентная ставка. Следовательно, к концу года реальная покупательная способность денежной единицы будет равна (1+ p)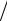 (1+ a), где (1+ p) – рост денежной единицы, обусловленный годовой процентной ставкой (если деньги вложены, например в банк). Таким образом, эффективная процентная ставка меньше номинальной, (1+ p) (1+ a) − 1 = ( p − a) (1+ a) < p. Для того, чтобы номинальная ставка P при годовой инфляции A обеспечивала увеличение реальной стоимости денежной единицы на величину q (в долях единицы), P должна удовлетворять уравнению
(1+ a), где (1+ p) – рост денежной единицы, обусловленный годовой процентной ставкой (если деньги вложены, например в банк). Таким образом, эффективная процентная ставка меньше номинальной, (1+ p) (1+ a) − 1 = ( p − a) (1+ a) < p. Для того, чтобы номинальная ставка P при годовой инфляции A обеспечивала увеличение реальной стоимости денежной единицы на величину q (в долях единицы), P должна удовлетворять уравнению
( p − a) (1+ a) = q, |
(1.13) |
из которого следует |
|
p = a + q(1+ a). |
(1.14) |
Пример 1.10. Инфляция составляет 10%. Какова должна быть номинальная годовая процентная ставка, чтобы эффективная ставка оказалась равной 13%? p = 0,10 + 0,13(1+ 0,10) = 0,243, т. е. P = 24,3%.♥
1.7. Денежные суммы S(t) и s(τ) в моменты t и τ называются эк-
вивалентными по ставке сравнения p сложных процентов, если
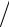
S(t) = s(τ)(1+ p)t−τ . |
(1.15) |
Это соотношение можно трактовать двояко: сумма s(τ), вложенная в
момент τ и наращиваемая по ставке p сложных процентов (см. (1.3) или (1.4)) к будущему моменту t (t > τ ) возрастет до значения S(t),
S(t) = s(τ)(1+ p)t−τ ; сумма s(τ) вкладывается в будущий момент вре-
мени τ (t < τ ) и процентная ставка p за истекший промежуток наращивалась по схеме сложных процентов, что равносильно вложению в
предшествующий момент t меньшей суммы S(t) = s(τ)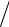 (1+ p)τ−t . Таким образом, эквивалентность сумм S(t) и s(τ) можно интер-
(1+ p)τ−t . Таким образом, эквивалентность сумм S(t) и s(τ) можно интер-
претировать следующим образом: “при движении в прошлое” (t > τ ) сумма S(t) уменьшается за каждый единичный промежуток в1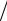 (1+ p)
(1+ p)
раз и к моменту τ превратится в s(τ),
s(τ) = S(t) (1+ p)t−τ . |
(1.16) |
Подобный пересчет будущей суммы к настоящему моменту называется приведением ее или нахождением ее современной величины, а формула сравнения денежных сумм в различные моменты вре-
мени – математическим дисконтированием.
Пример. 1.11. Что целесообразнее при ставке 12%: получить сегодня 1300 или через 6 лет 3000? Современный эквивалент вкладу в
3000 определяется выражением σ = 3000 / (1+ 0,12)6 1520 > 1300. Следовательно, целесообразнее получить через 6 лет 3000.♥
Аналогично можно ввести эквивалентность денежных сумм по ставке простых процентов (см. (1.1)–(1.2)),
S(t) = s(τ)(1+ (t − τ) p). |
(1.17) |
1.8. Обязательство в виде долговой расписки, гарантирующее выплату определенной денежной суммы в конкретный срок, называется векселем. Сумма, указанная в расписке, называется номиналом векселя. Учет векселя означает оплату векселя с дисконтом, т. е. со скидкой с его номинала (и возможно ранее указанного в векселе срока). Такой вексель затем может быть предъявлен к оплате подписавшему его субъекту.
Пример. 1.12. Произведен учет векселя номиналом S за 80% его стоимости за квартал до срока выкупа. Какова доходность этой опе-
рации? Старому владельцу векселя было выплачено 0,8S, а новый владелец получил через квартал сумму равную S. Следовательно, доходность нового владельца при учете векселя определяется величиной 0,3S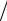 0,8S = 0,25 и составляет 25% за квартал.♥
0,8S = 0,25 и составляет 25% за квартал.♥
2.ПОТОК ПЛАТЕЖЕЙ, РЕНТА
2.1.Потоком платежей называется последовательность платежей и моментов времени, в которые они произведены. Платежи могут быть как положительными, так и отрицательными. Платеж со знаком плюс соответствует денежным поступлениям, а платеж со знаком минус – выплатам. Обычно предполагается, что процентная ставка P не изменяется в течение всего потока. Поток платежей называется конечным или бесконечным в зависимости от количества платежей.
Пусть R = lRk , τk q – поток платежей. Здесь Rk – платежи, τk –
моменты платежей. Величиной потока в момент t называется сумма платежей потока, дисконтированных к моменту t,
N |
|
R(t) = ∑Rk (1+ p)t−τk , |
(2.1) |
k=1
где суммирование производится по всем N моментам платежей и p = P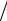 100.
100.
Величина R(0) называется современной величиной потока (в на-
чальный момент 0),
R(0) = ∑k Rk (1+ p)− τk , |
(2.2) |
а в величина R(tN ) – конечной величиной потока (в последний момент tN),
R(tN ) = ∑k Rk (1+ p)tN −τk . |
(2.3) |
Зная величину потока в некоторый момент времени t, можно найти поток в любой другой момент времени t′,
R(t′) = R(t)(1+ p)t′−t . |
(2.4) |
Так при t = 0 и t′ = τ N имеем |
|
R(τ N ) = R(0)(1+ p)τ N . |
(2.4а) |
