Факультатив

сумму cN = C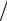N . К концу 1-го кредитного года с суммы C, которой пользовались весь год, нарастают проценты π1 = pC, и платеж будет равен r1 = c1 + π1 = CN + pC. К концу 2-го года будет выплаче-

на сумма r2 = C N + p(C − C N ) и т. д. Таким образом, к концу k-го года платеж будет равен rk = C N + p(C − (k − 1)C N ). Ряд r1,

r2,..., rN, составленный из платежей каждого года, определяет конечную убывающую арифметическую прогрессию с начальным r1 = C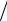N + pC и последним rN = C N + p C N элементами и с отрицательным шагом − pC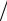N . Процентные деньги таrже определяются

наращенную величину процентных денег.

•Платежи по кредиту вносятся равными годовыми суммами r. Величина этой суммы может быть найдена, если процесс выплат рассматривать как выплаты по некоторой эквивалентной годовой ренте с платежом r и длительностью N лет. Для вычисления r, приравняем современную величину этой ренты (см. (2.11)) R(0) займу C,

C = rρ(N, P). Тогда r = C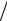ρ(N, P).

•Погашение кредита происходит несколько раз в год равными суммами r. Так как выплаты размером r деляют m раз в году, то всего выплат будет Nm на сумму Nmr. На эти выплаты начисляются про-

центы также m раз в год по ставке p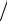m. Такие выплаты можно рассматривать как ренту (2.20), наращенная величина которой есть

R(N ) = rσ(Nm,Pm). Наращенная величина займа, в соответствии с (1.3), равна C(1+ p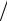n)Nm. Приравнивая эти величины друг другу, получим уравнение для r, C(1+ p n)Nm = rσ(Nm, P m), из которого

следует r = C(1+ p m)Nm 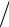σ(Nm, P m), где p = P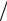100. !!!!!!!!

Приведенные ниже примеры иллюстрируют различные схемы погашения займа и показывают, что стоимость кредита (процентные деньги) существенно зависит от выбора этой схемы.

Пример 3.1. Рассмотрим кредит в 100 000, выданный на 5 лет под 10 сложных годовых процентов. Какова сумма платежа, отдаваемого за один прием по истечении срока кредита? По таблице 1.1 находим, M(512,) = 1,611. Следовательно, искомый платеж равен

161 100, а процентные деньги в нем составляют 61 100.♥

Пример 3.2. Параметры кредита из примера 3.1, основной долг займа выплачивается в конце срока кредитования, а проценты – ежегодно. Результат погашения займа показан в табл. 3.1. Всего по этому займу будет выплачено 150 000, из низ процентные деньги составля-

ют 50 000.♥

Таблица 3.1. Выплаты по кредиту

Пример 3.3. Параметры кредита из примера 3.1, основной долг займа выплачивается равными годовыми платежами r, а проценты – ежегодно πk. Результат погашения займа показан в табл. 3.2. По кредиту будет выплачено 130 000, причем суммарные процентные деньги равны 30 000.♥

Таблица 3.2. Выплаты по кредиту

Пример 3.4. Параметры кредита из примера 3.1, платежи по займу вносятся равными годовыми суммами. По таблице коэффициентов приведения годовой ренты (табл. 2.1) находим, ρ(512,) = 3791. . Поэтому ежегодный взнос равен R = 100 000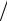ρ(512,) = 26 378,26. Таким образом, полный платеж по данному кредиту составит 131 900, а суммарные процентные деньги будут равны 31 900.♥

Пример 3.5. Параметры кредита из примера 3.1, погашение кредита происходит равными суммами m = 3 раз в году. В соответст-

вии с (2.10) имеем σ(5 3, P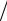3) = 3 (1+ 0,1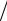3)5 3 − 1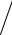0,1 = 19.06, из (1.3)

находим C(1+ p n)Nm = 100 000(1+ 0,1 3)5 3 =163 533,44 и, окончатель-

но, r = 163 533,44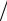19.06 = 8579,91. Следовательно, по кредиту будет возвращено 5 3r = 128698,71 и из них 28 698,71 – процентные деньги.♥

3.4. В дополнение к уже изложенным способам погашения займа рассмотрим ситуацию, когда заемщик имеет возможность создать фонд для погашения займа и получать на деньги этого фонда бо′льшие проценты Q, чем проценты P, под которые был взят кредит.

Допустим, что получен кредит на сумму C на N лет по ставке P сложных годовых процентов. В конце срока действия кредита платеж

“погасительный” фонд образуют ренту с годовым платежом R и годовой ставкой Q, причем Q > P, то к концу срока кредитования день-

ги фонда нарастут (см. (2.8)) до величины R(N ) = Rc(1+ q)N − 1h =

= Rσ(N,Q), где σ(N,Q) – коэффициент наращения годовой ренты

(2.10). Именно из этой суммы и будет погашен кредит в размере

C(1+ p)N .

Пример 3.6. Пусть C = 1000, N = 5, P = 10% и Q = 12%. Нара-

щенная за 5 лет сумма займа, учитывая значение M(510, ) мультиплицирующего множителя (табл. 1.1), равна S5 = 1000 1,611 = 1611. Принимая это значение за наращенную величину ренты R(5), найдем сумму годового платежа (используя табл. 2.2), R = S5 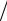σ(512,) =

=1611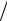6,353 = 253,6 в “погашающий” фонд.♥

3.5.Среди многообразия выдаваемых кредитов особую роль играет потребительский кредит. Обычно при получении потребительского кредита С на N лет начисляются простые проценты P (см. (1.1)), которые затем прибавляют к величине самого займа. Таким образом, сумма погашающих платежей определяется основным дол-

гом и процентными деньгами, начисленными на кредит, итого

C(1+ Np). Рассмотрим две наиболее часто используемые схемы погашения потребительского кредита.

Погашение кредита равными выплатами. Допустим, за год пре-

дусмотрено m выплат по кредиту. Тогда в течение всего срока кредита должно быть сделано Nm выплат. Следовательно, разовая величина выплаты равна C(1+ Np)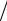Nm. В некоторых ситуациях полезно знать эквивалентную ставку сложного процента Q, по которой со-

временная величина потока выплат по кредиту C(1+ Np)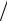Nm равна его номинальной величине C, т. е.

приближенное решение которого легко находится при помощи таблицы коэффициентов приведения годовой ренты (табл. 2.1).

Правило 78. Основной долг выплачивается равными долями, а процентные деньги в сумме NpC гасятся последовательными выплатами, уменьшающимися в арифметической прогрессии, причем последний платеж равен отрицательному шагу −d этой прогрессии. Так, если предусмотрено m выплат в течение года, т. е. всего Nm выплат, то первый и последний платежи будут Nmd и d соответственно. Следовательно, поток платежей описывается прогрессией d,2d,Κ , md,Κ Nmd , сумма которой (1+ Nm)Nmd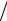2 должна быть равна процентным деньгам NpC, т. е. (1+ Nm)Nmd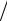2 = NpC. Это соотношение позволяет определить d, d = 2 pC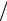(1+ Nm)m, а затем и весь поток выплат. Поток платежей по такой схеме выплат достаточно удобно рас-

3.6. Кредит называется льготным, если он выдается по льготной ставке, т. е. по ставке, которая меньше обычной. Это означает, что потребитель кредита практически получает субсидию, которая находится как разность современных значений итоговых погашающих платежей.

Допустим, что кредит размером C получен на N лет по льготной процентной ставке Q, которая меньше банковской ставки P. Если выплаты по займу будут производиться равными суммами, то такой поток платежей образует годовую ренту с платежом RQ. Современная

величина такой ренты (см. (2.11)) равна R(0) = C = RQρ(N,Q), где ρ(N,Q) – коэффициент приведения годовой ренты (см. (2.9) и табл.

определяет ежегодные потери кредитора.

Если рассмотреть годовую ренту с платежом RP − RQ, то современная величина потерь по ставке P будет равна

Эта величина указывает субсидию кредитора заемщику и называется

абсолютным грант-элементом, а множитель

1− ρ(N, P)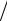ρ(N,Q)

– относительным грант-элементом.

Наращенная сумма субсидии, вычисленная по современной величине потерь (см. (2.7) и (1.6))

Вычислим современную величину потока выплат по льготной ставке

Q, RQ = 5000 ρ(10,9) = 5000 6,418 = 779,06 и по банковской ставке P,

RP = 5000 ρ(10,12) = 5000 5,650 = 884,96. Ежегодные потери кредито-

ра составляют 884,96 − 779,06 = 105,90. Относительный и абсолютный

ется величиной 598,32 M(10,12) = 598,32 3106, = 1858,3.♥

3.7. Кредит, выдаваемый под залог недвижимого имущества под небольшие проценты на несколько десятков лет, называется ипотечной ссудой. Если ипотечная ссуда не возвращается в установленный срок, то заложенное имущество становится собственностью кредитора. Часто ипотечная ссуда выплачивается равными месячными платежами, а на ее непогашенный остаток ежемесячно начисляются проценты. Такой поток платежей образует ренту с выплатами и начислением процентов 12 раз в году, т. е. m = n = 12 (см. §2.3).

Рассмотрим ипотечную ссуду размером C, выданную на N лет под P сложных процентов годовых, с ежемесячным платежом r. К концу N-го года наращенная величина потока рентных платежей достигнет значения (см. (2.20) и (2.10)) R( N ) = rσ(12N, P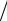12). С другой стороны, при начислении n =12 раз в год в течение N лет на исходную сумму C сложных P процентов годовых, итоговая сумма нарастет (см. (1.5а)) до величины CN = C M(12N, P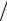12). Таким образом,

Найдем непогашенный остаток dk, соответствующий концу k-го года. В конце рассматриваемого года наращенная величина получен-

ной ссуды будет равна(см. (1.5)) C(1+ p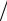12)12k , а наращенная сумма, обусловленная выплатами по ренте, – rσ(12k, P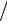12). Поэтому непогашенный остаток определяется как

nN = 12 30 = 360, P n = 3 12 = 0,25. Из (3.6) получаем, что ежемесячная выплата по кредиту равна r = C M(360,0,25)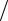σ(360,0,25). Вычислим непогашенный остаток, например к концу 20-го года. Тогда, nk = 12 20 = 240 и из (3.7) находим, dk = 200000 M(240,0,25) −

− rσ(240,0,25). Если под рукой нет таблиц значений для мультиплицирующих множителей M(360,0,25) и M(240,0,25) и коэффициентов наращения годовой ренты σ(360,0,25) и σ(240,0,25), то придется использовать явные формулы (3.9а) и (3.10а). Так,

r= 200000(1+ 0,0025)360 0,0025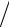((1+ 0,0025)360 − 1) =

=200000 2,4568 0,0025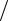1,4568 = 843,208

и

d20 = 200000(1+ 0,0025)240 − 843,208((1+ 0,0025)240 − 1)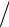0,0025 = = 364151,0 − 276826,9 = 87324,1.♥

3.8. Погашающие выплаты по кредиту, как и рентные платежи, можно при необходимости заменять на другие, эквивалентные платежи. Для замены потока выплат по займу необходимо подобрать такой новый поток платежей, современная величина которого будет равна современной величине потока выплат по исходному кредиту.

Пример 3.9. При получении кредита было установлено, что выплаты по нему должны происходить ежеквартально в сумме 10 000 в течение 6-и лет. Банковская ставка составляет 10% годовых. Через 3 года после получения кредита у заемщика возникла необходимость, в силу ряда объективных причин, погасить ссуду к концу 4-го года. Какова должна быть сумма ежеквартальных выплат за этот последний год? Современная величина непогашенного потока выплат определяется через коэффициент приведения годовой ренты (см. (2.11)), который определяется параметрами nN = 4 3 = 12 и P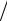n = 2,5, т. е.

Rρ(12,2,5) = 10000 10,25776 = 102577,6. Следовательно, в течение по-

следнего года ежеквартальный платеж определяется уравнением r ρ(4,2,5) = r 3,7619 = 102577,6, из которого находим r = 2726697. .♥

Несколько кредитов, как и несколько рент (см. §2.5), можно в суммировать или объединить в один кредит. Для этого необходимо сложить современные величины непогашенных остатков суммируемых займов. Полученная в результате сумма является современной величиной объединенного займа. Зная эту сумму, можно выбрать параметры объединенного займа, удовлетворяющие рассматриваемым экономическим условиям.

Пример 3.10. ♥

II.ОСНОВЫ ФИНАНСОВОГО АНАЛИЗА

4.ЭЛЕМЕНТЫ АНАЛИЗА ИНВЕСТИЦИОННЫХ ПРОЦЕССОВ

4.1.Основные понятия.

Рассмотрим некоторые основные понятия. Вложение капитала в экономический проект называется инвестицией. Пусть поток плате-

жей (см. §2.1) R = lRk , τk q определяет инвестиционный процесс. Здесь

Rk платеж в момент времени τk, причем, положительное значение Rk, Rk > 0, соответствует доходу от инвестиционного процесса, а отрицательное значение Rk, Rk < 0, – расходу, т.е. вложению в инвестиционный процесс или инвестиции. Предположим, что платежи делаются на стыке лет, имеющих неотрицательные номера, т. е. τk = k ≥ 0, где k – номер текущего года, и платеж делается на стыке k-го и (k+1)-го годов. Процесс, состоящий из конечного числа платежей, называется

конечным, в противном случае – бесконечным.

Приведенным чистым доходом NPV (Net Present Value) называ-

ется сумма всех платежей, дисконтированных к моменту 0 по приня-

В случае конечного процесса вводится понятие NFV (Net Future Value) – наращенный чистый доход – сумма всех платежей, дсконтированных к моменту τN последнего платежа по принятой в проекте

Доходностью inc инвестиционного процесса называется отношение чистого дохода к затратам, когда и тот, и другой дисконтируются по ставке P к произвольному моменту τ соответственно

характеризуется неотрицательной доходностью. Так как потоки платежей связаны соотношением (2.4), R(t′) = R(t)(1+ p)t′−t , то из неотрицательности R(t) следует неотрицательность R(t′) и наоборот. Поэтому очевидно, что инвестиционный процесс окупается, если сумма всех платежей, дисконтированных к произвольному моменту τj, положительна. Таким образом, инвестиционный процесс окупаем,

если приведенный чистый доход неотрицателен, NPV ≥ 0, и наоборот.

Введем срок окупаемости инвестиционнного процесса Kinv, как

В дальнейщем, если не оговаривается противное, будем рассматривать инвестиционные процессы с инвестицией (с вкладом) Inv только в момент 0, т. е. инвестиционный поток, у которого один отрицательный платеж R0 = − Inv , а все остальные платежи Rk положительны. В этом случае приведенный и наращенный чистые доходы определяются выражениями

k≥1

доходность инвестиционного процесса относительно нулевого момента равна

Для инвестиционного процесса, характеризуемого однократным вкладом Inv, вводится понятие внутренней доходности. Внутренняя доходность – такая наименьшая положительная процентная ставка Im, при которой сумма всех платежей, дисконтированных к моменту 0 по этой ставке, равна нулю,

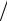im = Im100.

Если это уравнение имеет несколько корней, то выбирают наименьший из них.

Очевидно, что инвестиционный процесс всегда окупается при

Внутренней нормой доходности называется предельный уро-

вень годовой процентной ставки Pm, при которой взятые по этой ставке инвестиции окупаются доходами инвестиционного процесса, наращиваемыми по этой же ставке, !!!!!!!!!

Понятно, что для процессов с однократной инвестицией Pm = Im.

Пример 4.1. Пусть в рамках инвестиционного проекта в моменты τ0 делается вклад R0 = −20000, который в последующие N = 5 лет приносит доход Rk = 4000;5000;7000;8000;9000, при этом банковская годовая процентная ставка составляет 10%. Приведенный чистый доход

5

NPV = − Inv + ∑ Rk (1+ p)− k =

k=1

=−20000 + 4000 11, + 5000 1,21+ 7000 1,331+ 8000 1,464 + 9000 1,611 =

=−20000 + 3636,4 + 4132,2 + 5259,2 + 5464,1+ 5588,3 = 4080,2 > 0.

Следовательно, рассмотренный инвестиционный процесс самоокупаем. Наращенный чистый доход

5

NFV = − Inv (1+ p)5+∑ Rk (1+ p)5− k =

k=1

=−20000 1,611+4000 1,464+5000 1,331+7000 1,21+8000 11,+9000 1,611= = −32210,2 + 5856,4 + 6655 + 8470 + 8800 + 9000 = 6571,2.

Доходность инвестиционного проекта

inc = 4080,2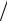20000 = 0,204,

т. е. составляет Inc = 20,4%. Внутренняя доходность Im находится как решение уравнения

R1 (1+ im ) + R2 (1+ im )2 + R3 (1+ im )3 + R4 (1+ im )4 + R5 (1+ im )5 = Inv.

Это уравнение может быть непосредственно решено на компьютере. Так, применяя процедуру “подбор параметра” из табличного процессора Excel, находим im = 0,1665 или Im = 16,65%.

Также решение этого уравнения легко может быть найдено при помощи достаточно простого итерационного процесса. Выберем ка- кое-либо значение для величены im в качестве начального приближения, например im,0 = 0,005. Подставляя im,0 в рассматриваемое урав-