
Факультатив
.pdf
Пример 2.1. Рассмотрим поток платежей R={(-3000,1); (2000,2); (4000,3)} при процентной ставке P = 13%. Современная величина по-
тока: R(0) = − 3000(1+ 0,13)−1+ 2000(1+ 013.)−2+ 4000(1+ 013.)−3=1683,63.
Конечная величина потока R(3) = R(0)(1+ 0,13)3 = 2429,30.♥
2.2. Рентой называется поток положительных платежей с постоянным временным шагом. В рамках ренты платежи часто являются также одинаковыми.
Конечной годовой рентой называется рента, характеризуется только одним платежом R в год, длительностью N лет и годовой процентной ставкой P. Обычно на рентные платежи начисляются сложные проценты. Рента называется постнумерандо, если платежи должны поступать в конце каждого промежутка, и называется пренумерандо, если платежи поступают в начале промежутка.
Пример 2.2. Рассмотрим 4-летнюю годовую ренту постнумерандо с платежом R = 2000 единиц и процентной ставкой P = 5%. В конце 1-го года вносится 2000. В конце 2-го года эта сумма увеличится на 260 за счет начисления процентов и на 2000 за счет очередного платежа, т. е. достигнет значения 2000(1+ 0,05) + 2000 = 4100. К концу 3-го года полная сумма возрастет до величины 4260(1+ 0,05) + 2000 = 6305. К концу 4-го года наращенная сумма будет равна 6813,80(1+ 0,05) + 2000 = 8620,25. Современная величина ренты находится в результате дисконтирования всей наращенной суммы к начальному моменту, R(0) = = 8620,25(1+ 0,05)−4 = 70919,.♥
При анализе конечной годовой ренты, характеризуемой параметрами ( R, N, P), обычно вычисляют ее современную величину (см.
(2.2)),
R(0) = R (1+ p)−1 + (1+ p)−2 +Κ +(1+ p)− N
(1+ p)−1 + (1+ p)−2 +Κ +(1+ p)− N 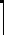 .
.
В скобках стоит сумма членов геометрической прогрессии с началь-
ным |
членом |
b = (1+ p)−1 |
и знаменателем |
прогрессии |
q = (1+ p)−1. |
|
|
1 |
|
|
|
Сумма N членов геометрической прогрессии дается формулами |
|||||
|
|
b (qN − 1) (q − 1) или (b q − b ) (q − 1), |
(2.5) |
||
|
|
1 |
N |
1 |
|
где b |
= (1+ p)− N – N-й член прогрессии. |
|
|
||
N
Учитывая первую из формул (2.5), получаем современную величину ренты

R(0) = R |
|
1− (1+ p)− N |
|
|
p |
(2.6) |
|||
|
|
||||||||
и, с ее помощью, итоговую к |
|
конечному |
моменту N сумму (см. (2.4)), |
||||||
называемую наращенной величиной ренты S, |
|
||||||||
R(N ) = R(0)(1+ p)N , |
|
(2.7) |
|||||||
которая также может быть представлена в виде |
|
||||||||
R(N ) = R |
|
(1+ p)N − 1 |
|
|
p. |
(2.8) |
|||
|
|
||||||||
Учитывая (2.7) видим, что положенная в настоящий момент в банк под P процентов годовых современная величина ренты R(0) к концу N-го года увеличится до наращенной величины ренты R(N ).
Коэффициент
ρ(N, P) = |
|
1− (1+ p)− N |
|
p |
(2.9) |
|
|
называется коэффициентом приведения годовой ренты, а коэффици-
ент
σ(N, P) = |
|
(1+ p)N − 1 |
|
p |
(2.10) |
называется коэффициентом наращения годовой ренты. Используя эти коэффициенты, получаем
R(0) = Rρ(N, P) |
(2.11) |
и |
|
R(N ) = Rσ(N, P). |
(2.12) |
Из (2.9)–(2.10) следует, что коэффициенты приведения ρ(N, P) и на- |
|
ращения σ(N, P) ренты связаны соотношениями |
|
σ(N, P) = ρ(N, P)(1+ p)N = ρ(N, P) M(N, P), |
(2.13) |
где M(N, P) – мультиплицирующий множитель (см. (1.6)). |
|
Коэффициенты приведения ρ(N, P) и наращения σ(N, P) показывают, во сколько раз современная и наращенная величины ренты больше ее годового платежа.
Формулы (2.6)–(2.13) формально могут использоваться при нецелых значениях N.
Коэффициенты приведения ρ(N, P) и наращения σ(N, P) годовой ренты даны в таблицах 2.1 и 2.2.
Таблица 2.1. Коэффициенты приведения годовой ренты ρ(N, P)
N \ P |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
3 |
2,829 |
2,775 |
2,723 |
2,673 |
2,624 |
2,577 |
2,531 |
2,487 |
2,444 |
2,402 |
4 |
3,717 |
3,630 |
3,546 |
3,465 |
3,387 |
3,312 |
3,240 |
3,170 |
3,102 |
3,037 |
5 |
4,580 |
4,452 |
4,329 |
4,212 |
4,100 |
3,993 |
3,890 |
3,791 |
3,696 |
3,605 |

6 |
5,417 |
5,242 |
5,076 |
4,917 |
4,767 |
4,623 |
4,486 |
4,355 |
4,231 |
4,111 |
7 |
6,230 |
6,002 |
5,786 |
5,582 |
5,389 |
5,206 |
5,033 |
4,868 |
4,712 |
4,564 |
8 |
7,020 |
6,733 |
6,463 |
6,210 |
5,971 |
5,747 |
5,535 |
5,335 |
5,146 |
4,968 |
9 |
7,786 |
7,435 |
7,108 |
6,802 |
6,515 |
6,247 |
5,995 |
5,759 |
5,537 |
5,328 |
10 |
8,530 |
8,111 |
7,722 |
7,360 |
7,024 |
6,710 |
6,418 |
6,145 |
5,889 |
5,650 |
Таблица 2.2. Коэффициенты наращения годовой ренты σ(N, P)
N \ P |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
3 |
3,091 |
3,122 |
3,153 |
3,184 |
3,215 |
3,246 |
3,278 |
3,310 |
3,342 |
3,374 |
4 |
4,184 |
4,246 |
4,310 |
4,375 |
4,440 |
4,506 |
4,573 |
4,641 |
4,710 |
4,779 |
5 |
5,309 |
5,416 |
5,526 |
5,637 |
5,751 |
5,867 |
5,985 |
6,105 |
6,228 |
6,353 |
6 |
6,468 |
6,633 |
6,802 |
6,975 |
7,153 |
7,336 |
7,523 |
7,716 |
7,913 |
8,115 |
7 |
7,662 |
7,898 |
8,142 |
8,394 |
8,654 |
8,923 |
9,200 |
9,487 |
9,783 |
10,089 |
8 |
8,892 |
9,214 |
9,549 |
9,897 |
10,260 |
10,637 |
11,028 |
11,436 |
11,859 |
12,300 |
9 |
10,159 |
10,583 |
11,027 |
11,491 |
11,978 |
12,488 |
13,021 |
13,579 |
14,164 |
14,776 |
10 |
11,464 |
12,006 |
12,578 |
13,181 |
13,816 |
14,487 |
15,193 |
15,937 |
16,722 |
17,549 |
Пример 2.2. Определим современную R(0) и наращенную R(N ) величины годовой ренты c платежом R = 5000 в год, длительностью N = 5 лет и годовой процентной ставкой P = 10%. Находим,
R(0) = 5000ρ(510,) = 5000
 1− (1+ 0,1)−5
1− (1+ 0,1)−5 

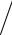 0,1 = 18953,9,
0,1 = 18953,9,
R(5) = Rσ(510,) = 5000
 (1+ 0,1)5 − 1
(1+ 0,1)5 − 1

 0,1 = 30525,5.♥
0,1 = 30525,5.♥
При использовании годовой ренты надо иметь в виду, что процентная ставка P, как правило, задается и не может быть изменена, а управляемыми (изменяемыми) параметрами могут быть платеж R ренты и ее длительность N. Однако вместо этих управляемых параметров в некоторых ситуациях удобно использовать современную R(0) и наращенную R(N ) величины ренты. Параметры R, N, P, R(0), R(N ) зависят друг от друга. Если заданы:
N и P, то R(0) и R(N ) вычисляются по (2.6) и (2.8);
P и R(0), то N = − ln(1− R(0) p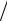 R)
R)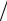 ln(1+ p) следует из (2.6);
ln(1+ p) следует из (2.6);
P и R(N ), то N = ln(R(N ) p R + 1)
R + 1)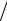 ln(1+ p) находится из (2.8);
ln(1+ p) находится из (2.8);
N , P и R(0), то R = R(0)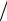 ρ(N, P) в соответствии с (2.6) или (2.11);
ρ(N, P) в соответствии с (2.6) или (2.11);
N , P и R(N ), то R = R(N )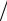 σ(N, P) согласно (2.8) или (2.12);
σ(N, P) согласно (2.8) или (2.12);
R, N и R(0), то желаемое значение P определяется из (2.6) или (2.11). Если N оказывается не целым, то N округляется, исходя из здравого смысла, до соответствующего целого. Так как (см. (2.11)) ρ(N, P) = R(0)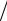 R, то приближенное значение N, зная P и R(0), также можно подобрать по таблице коэффициентов приведения годовой
R, то приближенное значение N, зная P и R(0), также можно подобрать по таблице коэффициентов приведения годовой

ренты ρ(N, P). Аналогично, так как (см. (2.12)) σ(N, P) = R(N ) R, то по P и R(N ) значение N находится из таблицы коэффициентов наращения годовой ренты σ(N, P). Что касается последнего из перечисленных выше пунктов, то решение уравнения (2.6) или (2.11) относительно желаемого значения P может быть получено численно. При этом заметим, что при малых P справедливо приближение ρ(N, P) N и, если R(0)
R, то по P и R(N ) значение N находится из таблицы коэффициентов наращения годовой ренты σ(N, P). Что касается последнего из перечисленных выше пунктов, то решение уравнения (2.6) или (2.11) относительно желаемого значения P может быть получено численно. При этом заметим, что при малых P справедливо приближение ρ(N, P) N и, если R(0) R ≥ N , то (2.11) не имеет решения, т. е. требуемой ставки P не существует. При R(0)
R ≥ N , то (2.11) не имеет решения, т. е. требуемой ставки P не существует. При R(0) R ≤ N процентную ставку P можно найти, например, решая уравнение (2.11), каким-нибудь итерационным способом.
R ≤ N процентную ставку P можно найти, например, решая уравнение (2.11), каким-нибудь итерационным способом.
Пример 2.3. Допустим, что R = 2000, P = 12%. Если современная величина ренты равна R(0) = 6000, то какова должна быть ее дли-
тельность? N = − ln(1− 6000 0,12 2000)
2000) ln(1+ 0,12) = 3,938 4. Другой способ, при ρ(N, P) = 6000
ln(1+ 0,12) = 3,938 4. Другой способ, при ρ(N, P) = 6000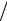 2000 = 3 и P = 12% из таблицы 2.1 находим, что N = 4.♥
2000 = 3 и P = 12% из таблицы 2.1 находим, что N = 4.♥
Пример 2.4. Пусть R = 2000, P = 12%. Наращенная величина ренты предполагается равной R(N ) = 20000. Какова должна быть ее длительность? N = ln(20000 0,12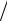 2000 + 1)
2000 + 1)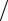 ln(1+ 0,12) = 6,957 7. Дру-
ln(1+ 0,12) = 6,957 7. Дру-
гой способ, при σ(N, P) = 20000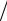 2000 = 10 и P = 12% из таблицы 2.2 находим, что N = 7.
2000 = 10 и P = 12% из таблицы 2.2 находим, что N = 7.
2.3. Рассмотрим конечную общую ренту с начислением процентов и платежами несколько раз за год, характеризующуюся годовым платежом R, годовой процентной ставкой P и длительностью N лет.
Допустим, платежи вносятся m, а проценты начисляются n раз в год через одинаковые интервалы. Тогда разовый платеж равен R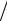 m. Предполагаем, что платежи вносятся и проценты начисляются в конце соответствующих интервалов. Если сделать очередной μ-й платеж, то остается (Nm − μ ) платежей, которые будут происходить в течение последующих (N − μ
m. Предполагаем, что платежи вносятся и проценты начисляются в конце соответствующих интервалов. Если сделать очередной μ-й платеж, то остается (Nm − μ ) платежей, которые будут происходить в течение последующих (N − μ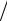 m) лет. За этот оставшийся период будет сделано
m) лет. За этот оставшийся период будет сделано 
 (N − μ
(N − μ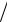 m)n
m)n начислений процентов по полной ставке p
начислений процентов по полной ставке p n, и возможно еще одно начисление по неполной ставке (здесь p = P
n, и возможно еще одно начисление по неполной ставке (здесь p = P 100, и квадратные скобки
100, и квадратные скобки  a
a означают целую часть числа a).
означают целую часть числа a).
Величина одного μ-го начисления равна !!!!!!!!!!!!!!!!!!!!!!!!
S |
= |
a |
R m 1+ p n (N −μ m)n . |
(2.14) |
|
μ |
|
fa |
f |
|
|

Суммируя всех такие начисления, найдем наращенную величину ренты
|
Nm |
|
|
|
|
Nm |
R m 1+ p n ( N −μ m)n . |
||||
R(N ) = |
∑ |
S |
μ |
= |
∑a |
||||||
|
|
|
|
fa |
f |
||||||
|
μ=1 |
|
|
|
|
μ=1 |
|
|
|
||
Меняя порядок суммирования, получим |
|
||||||||||
|
|
Nm−1 |
|
|
Nm |
R m 1+ p n (n m)μ . |
|||||
R(N ) = |
∑ |
S |
μ |
= |
∑a |
||||||
|
|
|
|
fa |
f |
||||||
|
|
μ=1 |
|
|
|
μ=1 |
|
|
|||
Полученная сумма есть сумма членов геометрической прогрессии с начальным членом R m, знаменателем a1+ p
m, знаменателем a1+ p nf(n
nf(n m) и числом членов Nm. Она равна (см. (2.5))
m) и числом членов Nm. Она равна (см. (2.5))
|
1 |
+ p n |
|
Nn − 1 |
|
|
||||||||
R(N ) = |
R |
|
a |
f |
|
|
|
. |
(2.15) |
|||||
m 1+ p n |
n m − 1 |
|||||||||||||
|
|
|
||||||||||||
|
|
|
|
a |
f |
|
|
|
|
|
|
|||
Используя коэффициент наращения годовой ренты (2.10), σ(N, P), |
||||||||||||||
имеем |
|
R |
|
σ(Nn, P n) |
|
|
|
|
||||||
R(N ) = |
|
. |
|
(2.16) |
||||||||||
|
|
|
||||||||||||
|
|
m σ(n m, P n) |
|
|
||||||||||
Зная наращенную величину ренты, вычислим ее современную вели-
чину (см. (2.7))
R(0) = R(N ) 1+ p n |
f |
− Nn. |
(2.17) |
a |
|
|
Соотношения (2.16)–(2.17) позволяют получить различные формулы для вычисления наращенной величины частных рент. Допустим, платежи осуществляются несколько раз в год (m > 1), а начисление процентов – один раз в год (n =1). В этом случае наращенная величина ренты равна
R(N ) = |
R |
|
σ(N, P) |
|
и R(0) = R(N ) 1+ p |
− N . |
(2.18) |
|||
|
|
|
||||||||
|
|
|
m σ(1 m, P) |
a |
f |
|
||||
|
|
|
|
|
|
|||||
Когда начисление процентов делается несколько раз |
за год |
|||||||||
(n > 1), а платеж – один раз в году (m = 1), получаем |
|
|
||||||||
R(N ) = R σ(Nn, P n) и R(0) = R(N ) 1+ p n − Nn . |
(2.19) |
|||||||||
|
|
|
σ(n, P n) |
|
a |
f |
|
|||
|
|
|
|
|
|
|
||||
Если число платежей и число начислений совпадают (m = n), то |
||||||||||
имеем |
|
|
|
|
|
|||||
R(N ) = |
R |
σ(Nn, P n) = |
R |
σ(Nn, P n) и R(0) = R |
ρ(Nn, P n). |
(2.20) |
||||
|
n |
|||||||||
|
n σ(1, P n) |
|
n |
|
|
|||||

где учитывается, что в силу (2.10), σ(1, P n) = 1.
n) = 1.
2.4. “Вечной” годовой рентой называется рента, в рамках которой предполагается, что последовательность платежей не ограничена во времени, т.е. выплачивается бесконечно долго. Хотя наращенная величина R(N ) такой ренты, как следует из (2.8), бесконечна, ее современная величина R(0) определяется бесконечным рядом дисконтированных к современному моменту платежей, который сходится к конечному пределу (см. (2.5)–(2.8)) и, таким образом, имеет смысл,
R(0) = R |
|
(1+ p)−1+ (1+ p)−2 + (1+ p)−3+Κ |
|
= lim R |
|
|
|
1− (1+ p)− N |
|
p = R p. |
|
|
|
|
|
|
|||||
|
|
|
|
N→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.21)
Пример 2.5. Аренда производственных помещений обходится в 50 000 при годовой процентной ставке 10%. Чему равна выкупная цена аренды? Выкупная цена может быть определена как современная величина всех будущих платежей. В соответствии с (2.21), она равна R(0) = 50000 0,10 = 500000. Если бы владелец помещений положил в банк 500 000 под 10% годовых по схеме простых процентов, то он получал бы 50 000 в год.♥
0,10 = 500000. Если бы владелец помещений положил в банк 500 000 под 10% годовых по схеме простых процентов, то он получал бы 50 000 в год.♥
2.5. Ренты можно суммировать (объединять) и заменять. Для получения суммарной ренты следует найти современные величины рент-слагаемых Rk (0), сложить их, R(0) = ∑k Rk (0), и, учитывая R(0),
подобрать для объединенной ренты остальные параметры N, P или R(N ) в соответствии с поставленными требованиями.
Для замены одной ренты другой рентой, но с новыми параметрами, необходимо вычислить современную величину R(0) первой ренты и, используя ее в качестве современной величины R′(0) другой (новой) ренты, R(0) = R′(0), подобрать для ее необходимые параметры.
Пример 2.6. Допустим, что рассматриваются три годовые ренты c длительностью Nk в 3, 5 и 9 лет с годовыми платежами Rk в 2000, 1000 и 500 соответственно и с одинаковой годовой процентной ставкой P = 5%. По таблице 2.1 найдем коэффициенты приведения годо-
вой ренты, ρ1(35,) = 2,723, ρ2(5,5) = 4,329 и |
ρ3(9,5) = 7,108. Следова- |
тельно, R1(0) = R1ρ1(35,) = 2000 2,723 = 5446, |
R2(0) = 1000 4,329 = 4329 |
и R3(0) = 500 7,108 = 3554. Поэтому современная величина объеди-
ненной ренты есть R(0) = R1(0) + R2(0)+ R3(0) = 5446 + 4329 + 3554=13329.
Далее, задавая один параметр, или N, или R(N ), вычислим второй.♥
3.ПРОСТЕЙШИЕ КРЕДИТНЫЕ РАСЧЕТЫ
3.1.Процедуры, связанные с заемом, кредитом или ссудой, являются древнейшими финансовыми операциями. Кредит (creditum) в переводе с латыни означает заем или ссуду. Кредитом называется получение денег или товаров в долг при условии их возврата, причем обычно кредит возвращают с процентами. Выдающий кредит называется кредитором, а получающий кредит – заемщиком.
Допустим, кредит C выдан (или заем C получен) на N лет под P сложных годовых процентов, p = P 100. Полученный заем также на-
100. Полученный заем также на-
зывается основным долгом, а проценты πk, начисляемые на остаток основного долга после предыдущего платежа, называются процентными деньгами. Таким образом, платеж rk по займу за k-й год может состоять из двух частей, суммы, идущей на выплату основного долга ck, и процентных денег πk, rk = ck + πk .
3.2. Рассмотрим общую схему погашения займа. Пусть
C = kck , τkp – поток платежей по основному долгу, в рамках которого ck – ежегодные (τk = 1) платежи могут быть различными.
В частном случае N = 2, в конце первого года в счет основного долга будет сделан платеж c1, а также будут начислены проценты π1 = pC за пользование кредитом C в течение этого года. Следовательно, платеж за первый год будет равен r1 = c1 + pC. Кроме этого, если эту сумму, например положить в банк в конце первого года, то кредитор за второй год получит на платеж r1 P процентов годовых, pr1, т. е. полученный платеж r1 нарастет до суммы r1 + pr1. В конце второго года платеж по основному долгу есть c2 = C − c1 и проценты по основному долгу за этот год – π2 = pc2 = p(C − c1), т. е.
r2 = (C − c1) + p(C − c1).
Окончательно, в течение двух лет по рассматриваемому кредиту с учетом всех процентов будет начислено
N =2 |
N =2 F |
F |
j−1 |
S2 = r1 + pr1 + r2 = ∑rj(1+ p)N − j = |
∑ Gc j + p C − ∑ck |
||
j=1 |
j=1 H |
G |
k=1 |
H |
|||
где платежи r1 и r2 представлены в виде
rj = c j + peC − ∑kj−=11ck j, j = 1,2.
II
JJ
KK
(1+ p)N − j ,
(3.1а)
(3.2а)
(В этой формуле подразумевается, что при j − 1 = 0 сумма равна нулю.) Так как r1 + pr1 = (c1 + pC)(1+ p) и r2 = (C − c1)(1+ p), то
S |
2 |
= (c + pC)(1+ p) + (C − c )(1+ p) = С(1+ p)2. |
(3.3а) |
|
|
1 |
1 |
|
|
Таким образом, величина S2 совпадает с наращенной суммой двухлетнего займа C, если бы он был положен в банк под P сложных процентов годовых (см. (1.3)).
Для того, чтобы сделать полученные формулы более понятными, рассмотрим еще один частный случай N = 3. Пусть в конце первого года сделан платеж по основному долгу c1 и по начисленным процентам π1 = pC, т. е. r1 = c1 + pC. Если выплаченную сумму r1 положить в банк под P годовых, то за второй год она нарастет до значения r1 + pr1 = p(c1 + pC), а за третий год – p(r1 + pr1) = p(c1 + pC)(1+ p).
Платеж за второй год равен по основному долгу c2, по процентам |
|||||||||
π2 = p(C − c1), |
т. е. r2 = c2 + p(C − c1). Сумма r2 в течение третьего года |
||||||||
может нарасти на величину pr2 = p( c2 |
+ p(C − c1)). За третий год пла- |
||||||||
теж состоит |
|
из |
величин |
c3 и |
π3 = pc3 = ( p(C − c1 − c2 )), |
т. е. |
|||
r3 = (C − c1 − c2 ) + ( p(C − c1 − c2 )). |
|
|
|
|
|
||||
Таким образом, платежи по трехлетнему займу C могут нарасти |
|||||||||
до значения |
|
|
|
|
|
N =3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
S3 = r1 + pr1 + p(r1 + pr1) + r2 + pr2 + r3 = ∑rj (1+ p)N − j = |
|
||||||||
|
|
N =3F |
|
|
j=1 |
|
|
|
|
|
|
|
j−1 |
I |
|
|
|
||
|
|
= |
∑ Gc j + pFC − ∑ck IJ(1+ p)N |
− j , |
(3.1б) |
||||
|
|
|
j=1 H |
G |
k=1 |
J |
|
|
|
где |
|
|
H |
KK |
|
|
|
||
|
rj = c j + peC − ∑kj−=11ck j, j = 1,2,3. |
|
|
||||||
|
|
|
(3.2б) |
||||||
Так как r + pr + p(r + pr ) = r (1+ p)2 и r + pr |
= r (1+ p), то груп- |
||||||||
|
1 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
|
пируя подобные члены в (3.1б), найдем, что наращенная сумма S3 трех летнего займа C
S |
= r (1+ p)2 |
+ r (1+ p) + r = C(1+ p)3. |
(3.3б) |
|
3 |
1 |
2 |
3 |
|
совпадает с наращенной суммой займа за три года, если бы он был положен в банк под P сложных процентов годовых (см. (1.3)).
Найденное свойство наращенной суммы S2 для двухлетнего (3.1а) и S3 трехлетнего (3.1б) потока платежей по займу C,
S2 = С(1+ p)2 и S3 = С(1+ p)3,
выполняется при получении займа C на произвольное число лет N:
наращенная сумма по N-летнему займу C определяется выражением
SN = С(1+ p)N , |
(3.3) |
причем справедливы следующие вспомогательные формулы
N |
|
SN = ∑rj (1+ p)N − j , |
(3.1) |
j=1 |
|
F |
j−1 |
I |
, j = 1,2,K, N . |
(3.2) |
rj = c j + π j = c j + pGC − ∑ck J |
||||
H |
k=1 |
K |
|
|
Формулы (3.1) и (3.2) очевидны в силу своего построения, кроме того формула (3.1) также обусловлена выражением (1.3).
Соотношение (3.3) можно доказать, используя математическую индукцию. Рассмотрим (3.3) в виде
N F |
F |
j−1 |
SN = ∑ Gc j + p C − ∑ck |
||
j=1 H |
G |
k=1 |
H |
||
II
JJ
KK
N
(1+ p)N − j = С(1+ p)N , C = ∑c j .
j=1
Это выражение, как было показано, справедливо для N = 2 и N = 3. Далее предполагая, что оно выполняется для произвольного N, докажем это выражение для N + 1. В самом деле имеем
N +1 F |
F |
~ |
j−1 |
SN +1 = ∑ Gc j + p C |
− ∑ck |
||
j=1 H |
G |
|
k=1 |
H |
|
||
II
JJ
KK
~ |
N +1 |
|
= ∑c j . |
||
(1+ p)N +1− j, C |
||
|
j=1 |
Проводя последовательно несложные преобразования, получаем
N +1 F |
|
j−1 |
I |
|
N +1 |
SN +1 = ∑ Gc j + pFC − ∑ck IJ(1 |
+ p)N +1− j + ∑ pcN +1(1+ p)N +1− j = |
||||
j=1 H |
G |
k=1 |
J |
|
j=1 |
H |
KK |
|
|||
N F |
|
j−1 |
I |
|
N +1 |
= (1+ p)∑ Gc j + pFC − ∑ck IJ(1 |
+ p)N − j + cN +1 + pcN +1 ∑(1+ p)N +1− j . |
||||
j=1 H |
G |
k=1 |
J |
|
j=1 |
H |
KK |
|
|||
Последнее слагаемое содержит сумму N + 1-го элемента геометриче-
ской прогрессии с начальным членом |
(1+ p)N +1 и знаменателем |
||||
(1+ p)−1, которая равна !!!!!!!!! |
|
|
|
|
|
N +1 |
1 |
+ (1 |
+ p) |
N +1 |
|
∑(1+ p)N +1− j = − |
. |
||||
p |
p |
||||
j=1 |
|
|
|||
|
|
|
|
||
Следовательно,
SN +1 |
= C(1+ p)N +1 + cN +1 |
− cN +1 |
+ cN +1(1+ p)N +1 = C(1+ p)N +1, |
|
|
|
~ |
что доказывает соотношение (3.3).
Из формулы (3.3) вытекает, что кредитору безразлично какими порциями возвращается основной долг, если кредит выдан под P сложных процентов годовых и возвращаемые суммы сразу же вкладываются в банк также под P сложных процентов годовых.
Общая сумма процентных денег, выплачиваемых заемщиком при возврате кредита, может быть найдена по формуле
N |
N F |
j−1 |
I |
N −1 |
|
∑ |
π j = p∑GC − ∑ck J |
= pNC − p ∑aN − jfc j . |
(3.4) |
||
j=1 |
j=1H |
k=1 |
K |
j=1 |
|
3.3. Существуют различные способы возвращения основного долга и процентных денег. Рассмотрим наиболее часто используемые:
•Весь кредит возвращается одним платежом rN в конце периода кредитования. К концу этого периода наращенная сумма займа будет равна C(1+ p)N , или C M(N, P), и она определяет требуемый пла-
теж, rN = C(1+ p)N . Здесь M(N, P) – мулитиплицирующий множи-
тель (см. (1.6)).
•Основной долг выплачивается в конце срока кредитования, а процентные деньги – ежегодно, в конце каждого года с момента выда-
чи займа. Тогда в конце первого года будет выплачена сумма
π1 = pC, то за заемщиком останется только основной долг C. Аналогичная ситуация повторится в конце следующего года, π2 = pC, и т. д. В итоге, в конце последнего N-го года заемщику необходимо выплатить rN = C + π N = C(1+ p). Таким образом, суммарные про-
центные деньги будут равны ∑k πk = NpC.
•Основной долг гасится равными ежегодными платежами cN. В конце каждого кредитного года заемщик вносит его N-ю долю, т. е.
