Поверхностные интегралы первого типа

Пусть - некоторая двусторонняя гладкая (или кусочно – гладкая) поверхность, ограниченная кусочно – гладким контуром. Пусть на этой поверхности (т.е. в каждой точке поверхности) определена функция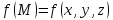.Разобьём поверхность 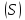с помощью сети произвольно проведённых кусочно-гладких кривых на части,…,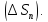Выбрав в каждой части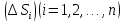произвольным образом одну точку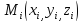, вычислим в этой точке значение функции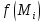=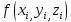и умножив его на площадь

,

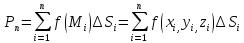которая называется интегральной суммой.

ОПРЕДЕЛЕНИЕ: Конечный предел этой интегральной суммы при бесконечном уплотнении разбиения поверхности , не зависящий ни от способа разбиения поверхности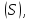ни от выбора точек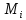в пределах каждой части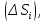называется поверхностным интегралом первого типа от функции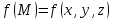по поверхности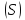и обозначается символом

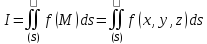,т.е.

.

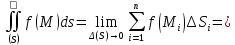
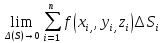ТЕОРЕМА. Пусть имеется незамкнутая гладкая поверхность 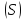заданная явным уравнением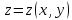. Положим, что прямые, параллельные оси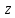пересекают поверхность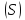, не более чем в одной точке, и пусть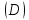проекция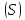на плоскость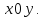

Тогда, какова бы не была функция 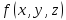, определённая в точках поверхности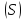и ограниченная:, имеет место равенство

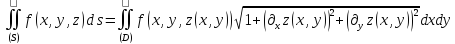
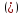
в предположении существования одного из этих интегралов (что влечет за собой и существование второго).

ЗАМЕЧАНИЕ. Так как 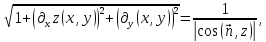то формулу (*) можно записать и так:.

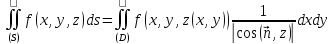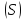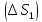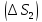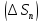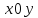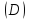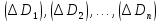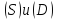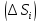Доказательство теоремы. Разложим поверхность на части,,…,с помощью сети произвольно проведённых кусочно – гладких кривых. Спроектируем линии разбиения на плоскостьи получим соответствующее расположение области:. Между построенными разложениями областейимеется то соответствие, что если к нулю стремятся диаметры частей, то к нулю стремятся диаметры частей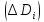инаоборот. Выберем в каждой части 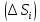точку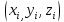и составим интегральную сумму

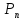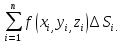=По определению=.

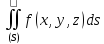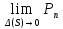В силу общей формулы для площади поверхности

=

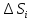Обозначим 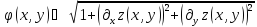, то есть=.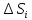

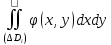По теореме о среднем, 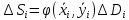, где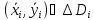, [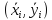- не произвольные, а фиксированные точки, определяемые теоремой о среднем].

В результате получим . Интегральная сумма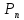отличается от интегральной суммы для интеграла: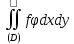

тем, что в 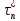значения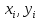произвольно в пределах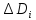, а в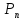значения аргумента функции 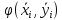фиксировано теоремой о среднем.

Рассмотрим 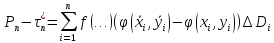. Пусть 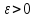– произвольно малое число. В силу равномерной непрерывности функции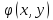при достаточно малых диаметрах областей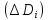будет

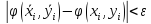. Отсюда следует, что , то есть

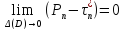. Так что .

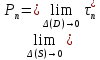Это значит, что из существования одного предела следует существование другого и обратно. По определению это означает, что

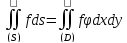, что и т. д.

ЗАМЕЧАНИЕ В частности двойной интеграл

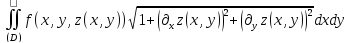существует в предложении непрерывности 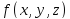. Напомним, что непрерывность функций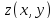,,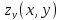предполагалось при определении поверхности (только тогда эта функция обозначалась как).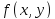

ЗАМЕЧАНИЕ Если 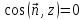или близок к нулю, или по каким-либо другим причинам, поверхностный интеграл первого типа можно с равным успехом выразить через проекции на другие координатные плоскости.

Именно, если 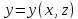, то.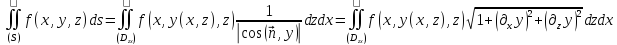

Или если 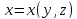, то.

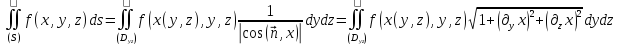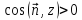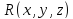СЛЕДСТВИЕ 1. Если , то для любой непрерывной ограниченной функциибудет справедливо равенство.

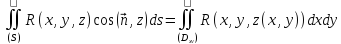Если 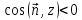, то

.

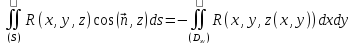Если 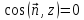, то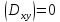, поэтому эти равенства справедливы и в этом случае.

Доказательство. В основной формуле

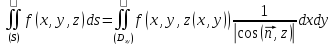
возьмём .

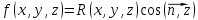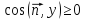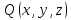СЛЕДСТВИЕ 2. Если , то для любой непрерывной ограниченной функциибудет справедливо равенство

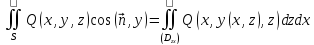
Если 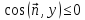, то

.

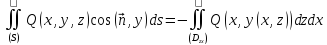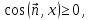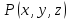СЛЕДСТВИЕ 3. Если то для любой непрерывной ограниченной функциибудет справедливо равенство

.

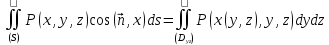Если 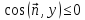, то

.

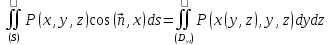ЗАМЕЧАНИЕ. В задачах математической физики часто возникает необходимость выразить поверхностный интеграл первого типа

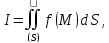
взятый по поверхности сферы радиуса 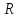в сферических координатах. Выведем соответствующую формулу. Рассмотрим отдельно верхнюю и нижнюю часть сферы. Они выражаются явной формулой:

Пусть

По формуле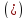

, .

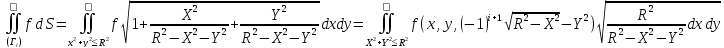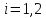На плоскости введем координаты:

,

,

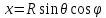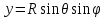(т.е. точка на плоскости рассматриваемая как проекция точки на сфере), и произведем замену переменных интегрирования.

Якобиан перехода

Кроме того

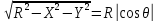
Для верхней половины

.

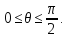
Для нижней половины с учетом того, что якобиан берется по абсолютной величине

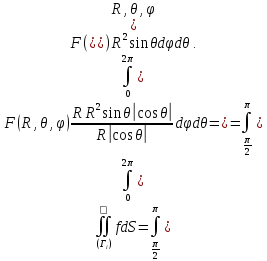
Складывая, получаем требуемую формулу: