
- •Поверхностные интегралы
- •Составители: с.Н. Алексеенко
- •Предисловие
- •Определение направляющих косинусов нормами
- •Площадь поверхности
- •Сторона поверхности
- •Орентация поверхности.
- •Поверхностные интегралы первого типа
- •Поверхностные интегралы второго типа.
- •Формула остроградского-гаусса
- •Формула интегрирования по частям
- •Формула грина
- •Формула стокса
- •Литература
- •Задания
Определение направляющих косинусов нормами
Пусть
имеется поверхность, уравнение которой
имеет вид
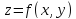 ,
,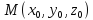 - произвольная точка на заданной
поверхности.
- произвольная точка на заданной
поверхности.
Пересечём
заданную поверхность плоскостью,
проходящей через заданную точку
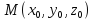 параллельно координатной плоскости
параллельно координатной плоскости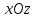 .
.
Уравнение
такой плоскости имеет вид
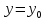 .
Пересечение поверхности
.
Пересечение поверхности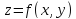 с плоскостью
с плоскостью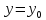 даёт некоторую кривую
даёт некоторую кривую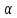 ,
параметрические уравнения которой
имеют вид:
,
параметрические уравнения которой
имеют вид: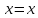 ,
,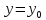 ,
,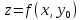 (здесь
(здесь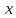 - параметр).
- параметр).
Вектор,
касательный к линии
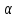 ,
будет иметь вид
,
будет иметь вид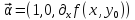 .
.
В
точке
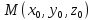 :
: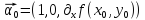 .
.
Также
пересечём поверхность
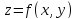 плоскостью
плоскостью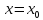 ,
через точку
,
через точку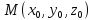 параллельно плоскости
параллельно плоскости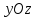 .
Пересечение поверхности
.
Пересечение поверхности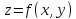 с плоскостью
с плоскостью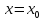 даёт
некоторую кривую
даёт
некоторую кривую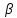 ,
параметрические уравнения которой
имеют вид
,
параметрические уравнения которой
имеют вид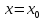 ,
, ,
,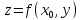 (Здесь
(Здесь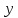 - параметр).
- параметр).
Вектор,
касательный к линии
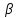 ,
будет иметь вид
,
будет иметь вид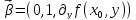 .
.
В
точке
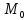 :
: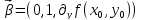 .
.
Вектор
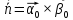 будет направлен по нормали в точке
будет направлен по нормали в точке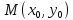 .
.
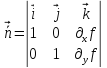 ,
,
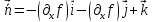 ;
;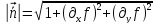 .
.
Искомый единичный вектор нормали, компоненты которого равны направляющим косинусам, будет иметь вид:
 ;
;
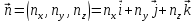 .
.
 ;
;
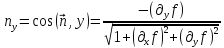 ;
;
 .
.
ЗАМЕЧАНИЕ.
Если взять
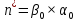 ,
то
,
то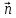 поменяет направление, а следовательно
перед радикалами поменяются знаки. Т.
е. в общем виде надо перед радикалами
ставить «±».
поменяет направление, а следовательно
перед радикалами поменяются знаки. Т.
е. в общем виде надо перед радикалами
ставить «±».
Площадь поверхности
Предварительно рассмотрим искажение площади при проектировании плоских областей.

Пусть
плоскости
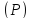 и
и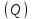 образуют между собой двугранный угол
образуют между собой двугранный угол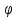 ,
т. е.
,
т. е.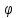 - это угол между двумя нормалями,
проведёнными в каждой из плоскостей к
общей точке на линии пересечения
- это угол между двумя нормалями,
проведёнными в каждой из плоскостей к
общей точке на линии пересечения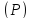 и
и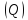 .
.
Обозначим
линию пересечения через
 .
.
Пусть
на плоскости
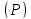 задана прямоугольная область
задана прямоугольная область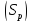 ,
у которой одна сторона параллельна
линии
,
у которой одна сторона параллельна
линии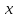 ,
а другая перпендикулярна
,
а другая перпендикулярна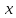 .
Спроектируем область
.
Спроектируем область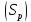 на плоскость
на плоскость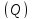 .
На плоскости
.
На плоскости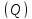 образуется прямоугольная область
образуется прямоугольная область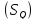 ,
у которой тоже одна сторона будет
параллельна
,
у которой тоже одна сторона будет
параллельна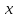 ,
а другая перпендикулярна
,
а другая перпендикулярна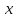 .
Обозначим сторону
.
Обозначим сторону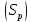 параллельную
параллельную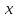 через
через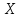 ,
а сторону перпендикулярную
,
а сторону перпендикулярную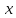 через
через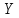 .
Для соответствующих сторон
.
Для соответствующих сторон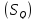 ,
которые мы обозначим через
,
которые мы обозначим через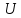 ,
,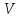 ,
будем иметь
,
будем иметь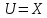 ,
,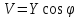 .
А тогда
.
А тогда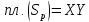 ,
, ,
или
,
или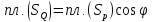 .
.
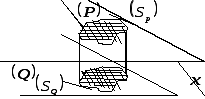 Пусть
теперь на плоскости
Пусть
теперь на плоскости
 задана криволинейная область
задана криволинейная область .
Спроектируем её на плоскость
.
Спроектируем её на плоскость .
Обозначим проекцию через
.
Обозначим проекцию через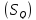 .
Разобьем область
.
Разобьем область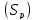 прямыми линиями, параллельными и
перпендикулярными линии
прямыми линиями, параллельными и
перпендикулярными линии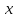 ,
на некоторое число подобластей. При
достаточно мелком разбиении большинство
из подобластей будут представлять собой
прямоугольники.
,
на некоторое число подобластей. При
достаточно мелком разбиении большинство
из подобластей будут представлять собой
прямоугольники.
Тогда
площадь
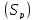 будет приблизительно равна сумме
площадей прямоугольников, целиком
принадлежащих
будет приблизительно равна сумме
площадей прямоугольников, целиком
принадлежащих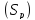 :
:
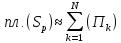 .
.
Спроектировав
линии разбиения на плоскость
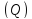 ,
разобьём область
,
разобьём область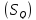 на соответствующее число подобластей,
из которых будет
на соответствующее число подобластей,
из которых будет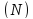 прямтугольников.
прямтугольников.
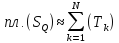 .
.
Причем
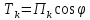 ,
откуда следует
,
откуда следует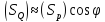 .
.
При
всё более мелком разбиении области
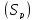 на прямоугольники, получим
на прямоугольники, получим
 .
.
Соответственно
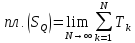 .
Так как для каждой из подобластей
справедливо равенство
.
Так как для каждой из подобластей
справедливо равенство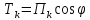 ,
где
,
где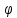 не зависит от
не зависит от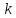 ,
то приходим к
,
то приходим к :
:
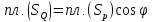 .
.
Выведем это соотношение ещё раз через преобразование интегралов.
Пусть
на плоскости
 задана декартовая система координат,
у которой одна ось совпадает с линией
пересечения плоскостей
задана декартовая система координат,
у которой одна ось совпадает с линией
пересечения плоскостей и
и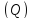 ,
а другая перпендикулярна ей. Пусть это
оси
,
а другая перпендикулярна ей. Пусть это
оси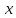 и
и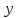 .
Тогда
.
Тогда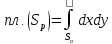 .
Спроектируем оси изменения
.
Спроектируем оси изменения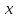 и
и на плоскость
на плоскость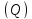 .
Обозначим проекции
.
Обозначим проекции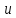 и
и .
Введём на осях те же единицы длины, что
и на осях
.
Введём на осях те же единицы длины, что
и на осях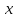 и
и .
.
Длина
любого отрезка на оси
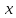 при этом совпадает с длиной любого
отрезка на оси
при этом совпадает с длиной любого
отрезка на оси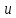 .
Следовательно, при таком проектировании
для координаты
.
Следовательно, при таком проектировании
для координаты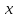 любой точки на
любой точки на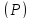 и соответствующей ей при проектировании
координате
и соответствующей ей при проектировании
координате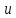 точки на
точки на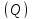 будем иметь
будем иметь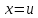 .
.
В
то же время, для координаты
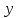 любой точки на
любой точки на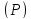 и соответствующей ей при проектировании
координате
и соответствующей ей при проектировании
координате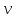 точки на
точки на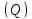 будет выполняться соотношение
будет выполняться соотношение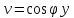 .
Это означает, что при таком проектировании
происходит преобразование координат
.
Это означает, что при таком проектировании
происходит преобразование координат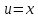 ,
,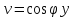 .
.
Имеем
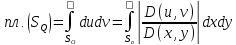 .
.
Подсчитаем
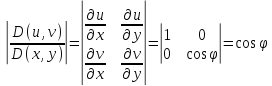 ,
отсюда получим
,
отсюда получим
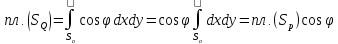 .
.
Таким образом, при проектировании площадь плоской фигуры умножается на косинус угла между той плоскостью, с которой проектируется и той, на которую проектируется.
Определим
теперь для произвольной поверхности
понятие площади.
Ограничимся случаем, когда уравнение
поверхности имеет вид
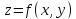 .
.
 Положим,
что цилиндр
Положим,
что цилиндр
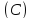 проектирует заданную поверхность
проектирует заданную поверхность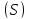 на плоскость
на плоскость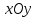 в виде области
в виде области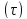 .
Разобьём площадь
.
Разобьём площадь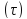 на малые элементы
на малые элементы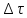 .
Цилиндры, построенные на основаниях
.
Цилиндры, построенные на основаниях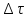 ,
разобьют
,
разобьют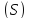 на элементы
на элементы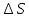 .
.
Возьмем
в каждом из элементов
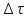 по точке
по точке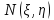 ,
которой соответствует на поверхности
,
которой соответствует на поверхности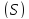 точка
точка ,
где
,
где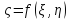 .
.
Проведем
в точке
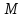 касательную плоскость и нормаль
касательную плоскость и нормаль к поверхности, и обозначим через
к поверхности, и обозначим через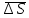 плоскую площадку, вырезаемую на этой
касательной плоскости цилиндром с
основанием
плоскую площадку, вырезаемую на этой
касательной плоскости цилиндром с
основанием .
.
ОПРЕДЕЛЕНИЕ.
Площадью поверхности
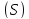 назовем предел суммы площадей плоских
площадок
назовем предел суммы площадей плоских
площадок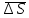 при бесконечном уплотнении разбиения
области
при бесконечном уплотнении разбиения
области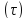 ,
т.е. когда число элементов
,
т.е. когда число элементов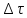 бесконечно растет, а каждый из них
бесконечно уменьшается по всем
направлениям.
бесконечно растет, а каждый из них
бесконечно уменьшается по всем
направлениям.
В
дальнейшем переход к пределу при
бесконечном уплотнении разбиения
некоторой области (Q)
будем обозначать символом (Q)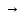 0.
0.
Покажем,
что когда
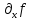 и
и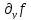 являются непрерывными функциями, то
этот предел существует и выражается
двойным интегралом по области
являются непрерывными функциями, то
этот предел существует и выражается
двойным интегралом по области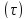 .
.
Элементы
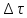 есть проекция плоского элемента
есть проекция плоского элемента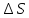 на плоскость
на плоскость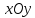 ,
причем нормали к плоскостям, в которых
лежат эти две плоские площадки
,
причем нормали к плоскостям, в которых
лежат эти две плоские площадки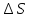 и
и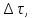 составляют угол
составляют угол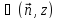 .
Следовательно, угол между самими
плоскостями тоже равен
.
Следовательно, угол между самими
плоскостями тоже равен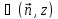 .
.
Следовательно
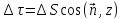 ,отсюда
следует
,отсюда
следует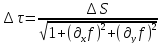 .
Берем нормаль в ту сторону, чтобы
.
Берем нормаль в ту сторону, чтобы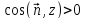 .
То есть если
.
То есть если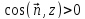 ,
то
,
то .
.
Таким
образом, для площади
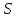 ,
рассматриваемой поверхности
,
рассматриваемой поверхности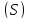 ,
мы имеем по определению:
,
мы имеем по определению:
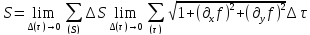 .
.
В
случае непрерывных
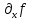 и
и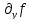 предел, стоящий в правой части равенства,
существует и представляет собой двойной
интеграл по области
предел, стоящий в правой части равенства,
существует и представляет собой двойной
интеграл по области .
.
Получим
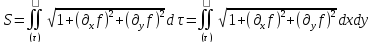 .
.
Этим доказано существование площади и установлено её выражение.
Можно написать формулы для площади и так:
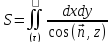 ,
считая угол
,
считая угол
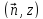 острым.
острым.
Или
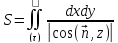 ,
если не требовать, чтобы угол
,
если не требовать, чтобы угол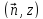 был острым.
был острым.
Нужно
брать абсолютное значение
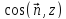 ,
т.к. площадь считается величиной
положительной.
,
т.к. площадь считается величиной
положительной.
Выражение
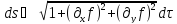 называется элементом площади поверхности.
называется элементом площади поверхности.
Если
на заданной поверхности в заданной
системе координат есть такие участки,
где
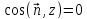 ,
то для определения площади таких участков
надо или проектировать их на другие
координатные плоскости, или изменять
систему координат.
,
то для определения площади таких участков
надо или проектировать их на другие
координатные плоскости, или изменять
систему координат.
Скажем,
есть участок поверхности, где
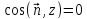 и где уравнение поверхности можно
записать в виде
и где уравнение поверхности можно
записать в виде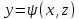 ,
то площадь такого участка можно определить
через его проекцию на координатную
плоскость
,
то площадь такого участка можно определить
через его проекцию на координатную
плоскость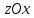 .
Тогда
.
Тогда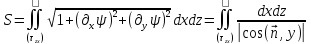 .
.
