Распределенные нагрузки

На практике часто вместо сосредоточенных сил сталкиваются с нагрузками, распределенными по поверхностям, по тому или иному закону. В этом случае вводится понятие интенсивности распределенной нагрузки . В зависимости от того, по какой поверхности распределены силы, интенсивностьможет иметь размерность:,,. Рассмотрим нагрузку, распределенную по длине для различных случаев.

28

1. Равномерно распределенная нагрузка вдоль отрезка прямой ()

В этом случае силы, равномерно распределены вдоль отрезка прямой . Для такой системы сил интенсивность имеет постоянное значение. При расчетах эту систему сил нужно заменить равнодействующей(рис. 31).Общее правило замены распределенной нагрузки сосредоточенной силой: модуль сосредоточенной силы численно равен площади фигуры, которую образует распределенная нагрузка, а линия действия этой силы проходит через центр тяжести фигуры, которую образует данная распределенная нагрузка.

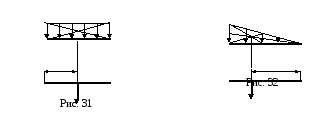Применяя это правило к схеме, показанной на рис. 31, получаем, что и проходит эта сила через центр тяжести прямоугольника ,т.е. через точку пересечения диагоналей, и делит сторону пополам.

2. Нагрузка, распределенная вдоль отрезка по линейному закону

В этом случае силы распределены вдоль отрезка прямой по линейному закону, т.е. интенсивность меняется от нуля до(рис. 32). Примером такой нагрузки могут служить силы давления воды, распределенные по высоте какого-либо не полностью погруженного тела. Действуя по процедуре описанной выше, также заменяем эту распределенную нагрузку сосредоточенной силой: . Проходит эта сила через центр тяжести треугольника ,т.е. через точку пересечения медиан, и делит высоту в отношении от основания и от вершины .

3. Нагрузка, распределенная вдоль отрезка прямой по произвольному закону

Такой вид нагрузки показан на рис. 33,а. Требуется заменить эту нагрузку сосредоточенной силой , определив ее точку приложения по процедуре описанной ранее. Для примера примем, что интенсивностьзависит от длины распределения, т.е.. Покажем, как можно сделать переход от схемы 33,а к схеме 33,б.

29

Первую часть задачи, т.е. определение модуля силы можно решить следующим образом. Разбиваем произвольную фигуру, показанную на рис. 33,а, на ряд бесконечно малых прямоугольников длиной . Модуль сосредоточенной силы от этой элементарной нагрузки будет равен . Переходя от элементарных фигур к фигуре, показанной на рис. 33,а берем интеграл по длине :.

Теперь переходим ко второй части задачи, т.е. определяем точку приложения этой силы. Для этого воспользуемся теоремой Вариньона. Применительно к данным схемам она будет выглядеть следующим образом: . Разбиваем произвольную фигуру, показанную на рис. 33,а, на ряд бесконечно малых прямоугольников длиной . Модуль сосредоточенной силы от этой элементарной нагрузки будет равен . Определяем момент этой силы относительно точки:. Тогда. Но, с другой стороны, если посмотреть на рис. 33,б, то . Приравнивая правые части полученных равенств, получаем выражение для : , отсюда.

4. Нагрузка, равномерно распределенная по дуге окружности

Примером такой нагрузки могут служить силы давления жидкости на боковые стенки цилиндрического сосуда (рис. 34).

Из симметрии видно, что сумма проекций этих сил на ось равна нулю. Следовательно, их равнодействующая направлена вдоль оси .

30

По модулю

,

г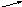де- сила, действующая на элемент дуги длиной,- угол, образуемой этой силой с осью . Из рис. 34 видно, что , тогда, вынося общий сомножительза знак суммы, получаем. Окончательно, где- длина хорды, стягиваемой дугою.