Пространство в механике рассматривается, как трехмерное, а время считается универсальным, т.е. протекающим одинаково во всех системах отсчета. Время является скалярной, непрерывно меняющейся величиной. В задачах кинематики оно принимается за независимую переменную (аргумент), а все остальные величины (координаты, скорости и т.д.) рассматриваются как функции этого аргумента.

Кинематику делят на кинематику точки и кинематику системы материальных точек (тела). В кинематике решаются две основные задачи:

- первая задача состоит в установлении математических способов задания движения точек или тел;

- вторая задача заключается в том, чтобы, зная закон движения данного тела или точки, определить все кинематические величины, характеризующие как движение тела в целом, так и движение каждой из его точек в отдельности.

Для решения задач кинематики необходимо, чтобы непосредственно был задан или закон движения данного тела, или же закон движения, какого-нибудь другого тела, кинематически связанного с данным.

Способы задания движения точки

Чтобы задать движение точки, надо задать ее положение по отношению к выбранной системе отсчета в любой момент времени. Для этого задания можно применять один из трех способов: естественный, координатный, векторный.

1. Естественный способ задания движения точки

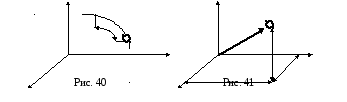
Естественным способом задания движения пользуются в тех случаях, когда траектория движущейся точки известна заранее. Непрерывная линия, которую описывает движущаяся точка относительно данной системы отсчета, называется траекторией точки. Если траектория является прямой линией, то движение точки называется прямолинейным, а если кривой линией – то криволинейным.

Пусть точка движется относительно системы отсчета вдоль некоторой траектории (рис. 40). Выберем на этой траектории какую-нибудь неподвижную точку , которую примем за начало отсчета, а затем, рассматривая траекторию как координатную ось, установим на ней положительное и отрицательное направление, как на обычной координатной оси.

39

Тогда положение точки на траектории будет однозначно определяться криволинейной координатой , равной расстоянию от точки до точки , измеренному вдоль дуги траектории и взятому с соответствующим знаком. При движении точка будет перемещаться вдоль траектории, следовательно, расстояние будет с течением времени изменяться. Чтобы определить положение точки на траектории в любой момент времени, надо знать зависимость вида:

. (13)

Это уравнение выражает закон движения точки. Таким образом, чтобы задать движение точки естественным способом, необходимо знать:

1. Траекторию движения точки;

2. Начало отсчета на траектории с указанием положительного и отрицательного направлений отсчета;

3. Закон движения точки вдоль траектории .

Следует отметить, что величина определяет положение точки, а не пройденный ей путь. Например, если точка, двигаясь из начала отсчета, доходит до положения , а затем, двигаясь в обратном направлении, приходит в положение , то в этот момент ее координата , а пройденный за это время путь будет равен.

2.Координатный способ задания движения точки

В этом случае положение движущейся точки в пространстве определяют тремя ее декартовыми координатами относительно выбранной неподвижной прямоугольной системы (рис. 41). При движении точки эти координаты являются однозначными и непрерывными функциями времени, т.е. уравнения движения получают в виде

, ,.(14)

При координатном способе задания движения точки траектория в непосредственном виде не дается, но может быть получена из уравнений движения. Исключая из уравнений движения время, получаем два соотношения между координатами , которые определяют линию, описываемую в пространстве движущейся точкой, т.е. ее траекторию.

Если движущаяся точка остается за все время движения в одной и той же плоскости, то, приняв эту плоскость за координатную , получаем два уравнения движения,.

Уравнения движения точки в координатной форме представляют собой уравнение траектории в параметрической форме, где за независимый параметр принято время. Исключая его из уравнений движения, получаем уравнение траектории.

При движении точки в плоскости можно пользоваться не только декартовыми координатами. В этом случае можно ввести в рассмотрение полярные координаты (рис. 42).

40

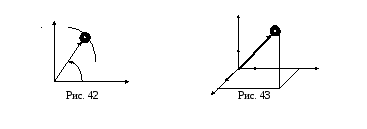
Положение точки в этом случае будут определять полярными координатами и, т.е. уравнения движения точки вполярных координатах имеют вид .