Тема 7. Пространственная система сил

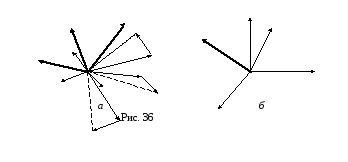
Пусть на тело действует произвольная система сил ,, …,, расположенных в пространстве (рис. 36,а). Возьмем произвольную точку , которую назовемцентром приведения, и по аналогии, как и для плоской системы, приведем все эти силы к центру (рис. 36,б). В результате в центре получаем:

1. Систему сходящихся сил, складывая которые получаем главный вектор системы .

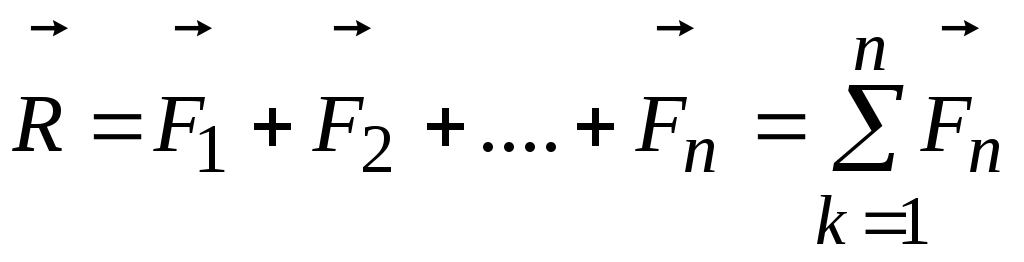2. Пространственную систему присоединенных пар, вектора – моменты которых равны: , , …, .

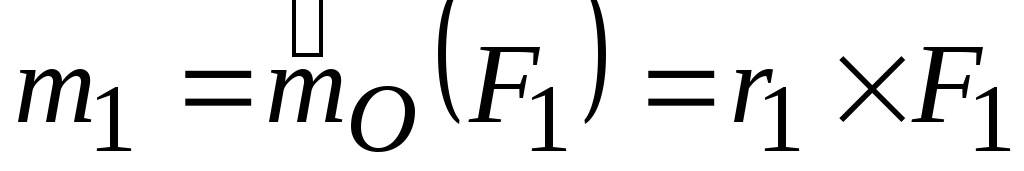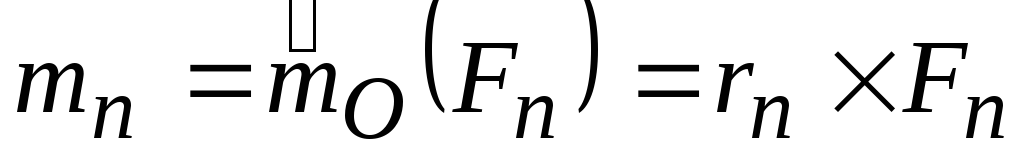33

Сложим геометрически вектора – моменты присоединенных пар. В результате система пар заменится одной парой, вектор – момент которой будет равен или . Величина , равная геометрической сумме векторов – моментов всех сил относительно центра , называетсяглавным моментом системы сил относительно этого центра.

Определим проекции этих двух векторов на координатные оси:

, ,

, .

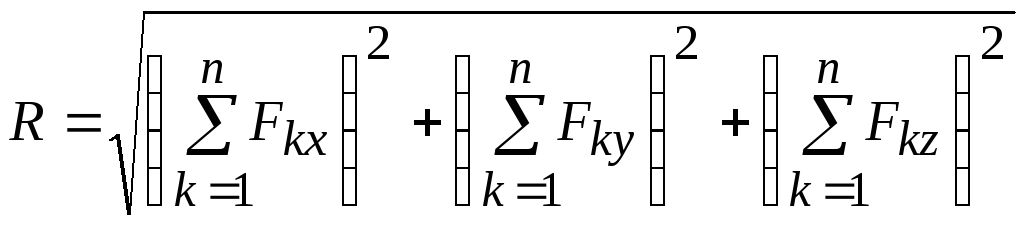Направление главного вектора определяют направляющие косинусы :

.

,,,

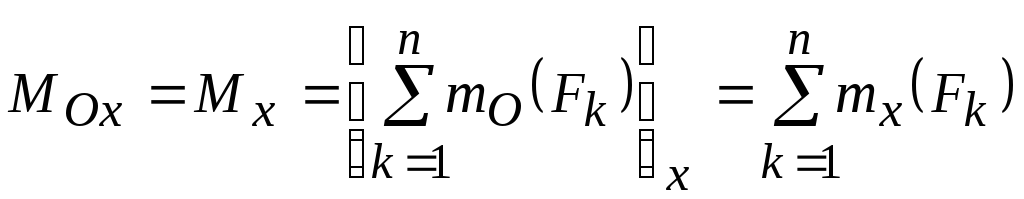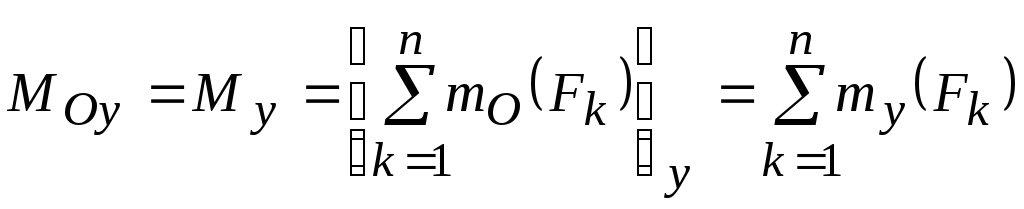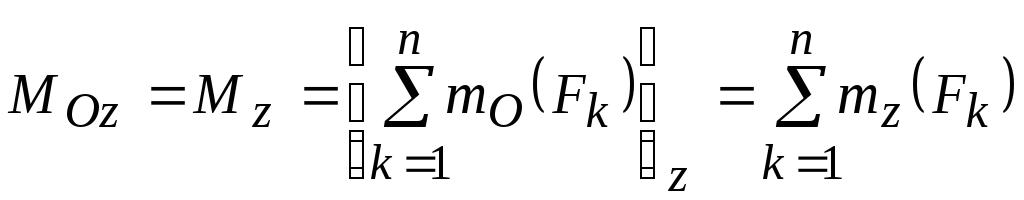34

.

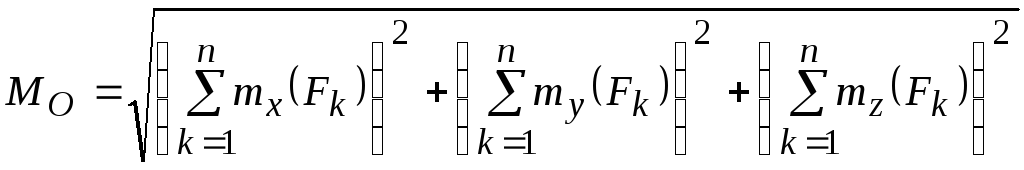Направление главного момента определяют направляющие косинусы: .

Рассмотрим теперь, к каким простейшим видам можно привести пространственную систему сил.

1. Если для данной системы сил 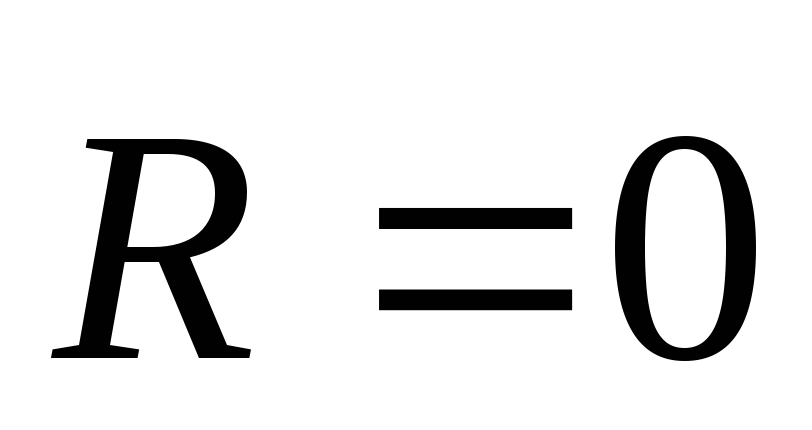, а 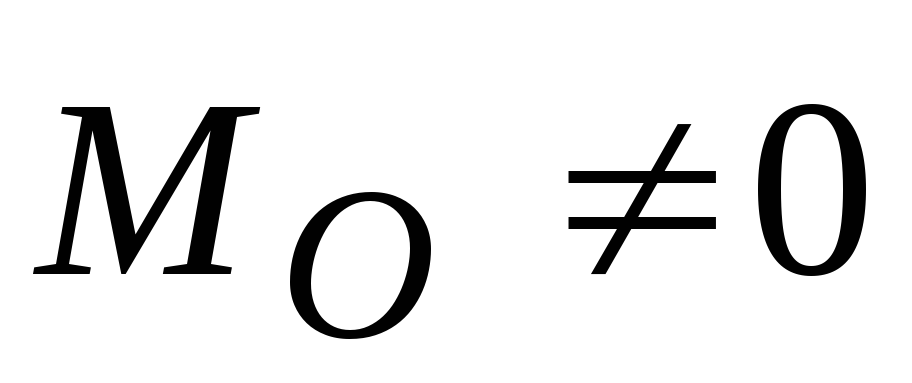, то онаприводится к одной паре с моментом . Причем в этом случае величина 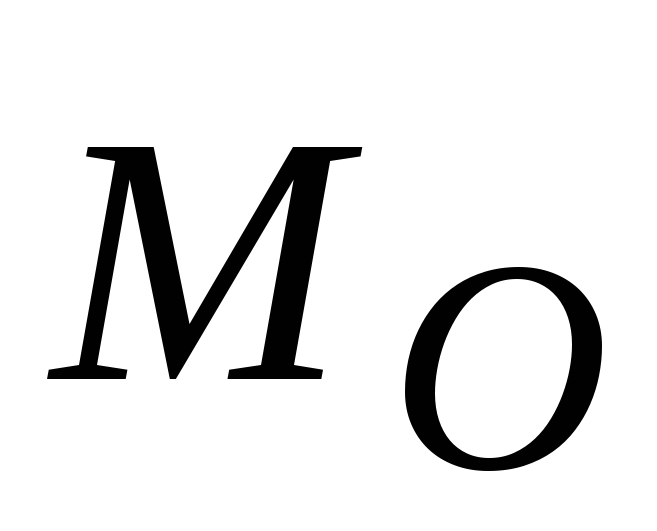не зависит от центра приведения, так как иначе мы получили бы, что одна и та же система сил заменяется разными, не эквивалентными друг другу. парами, что невозможно.

2. Если для данной системы сил 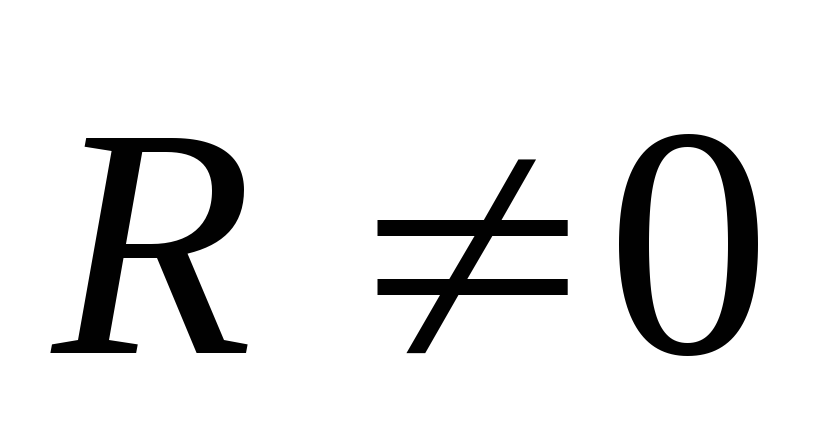, то здесь появляются следующие варианты приведения:

а) , . В этом случае система сразу заменяетсяравнодействующей, которая в данном случае будет равна главному вектору системы и проходит через точку .

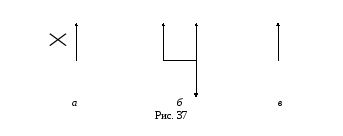б) , и. В этом случае система также заменяетсяравнодействующей, которая будет равна главному вектору системы, но проходить она будет не через точку , а через точку. Покажем, что это действительно так и определим положение точки. Пусть в результате приведения, система привелась к главному векторуи главному моментуотносительно центра(рис. 37,а).

Пару сил изобразим силами и, причем эти силы подбираем таким образом, чтобы у нас выполнялись равенства:,(рис. 37,б).

35

Затем отбрасываем силы икак уравновешенные и получаем, что система заменяется равнодействующей, но проходящей через точку(рис. 37,в). Положение точки определится соотношением.

3. Приведение к динамическому винту. Если в результате приведения система привелась и к главному вектору и главному моменту, причем угол между ними л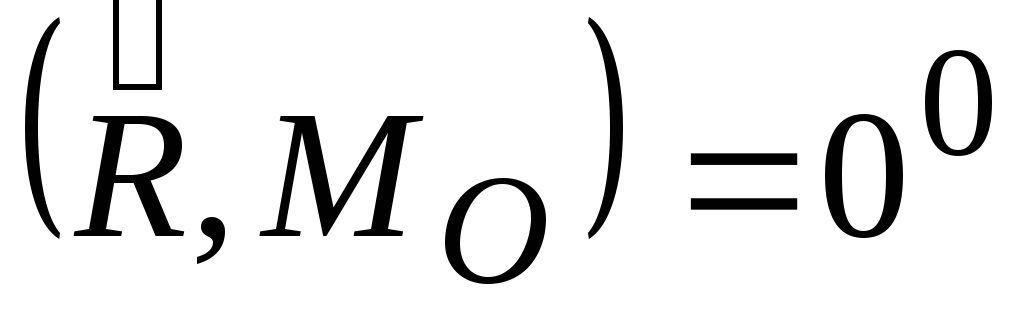ибо , либо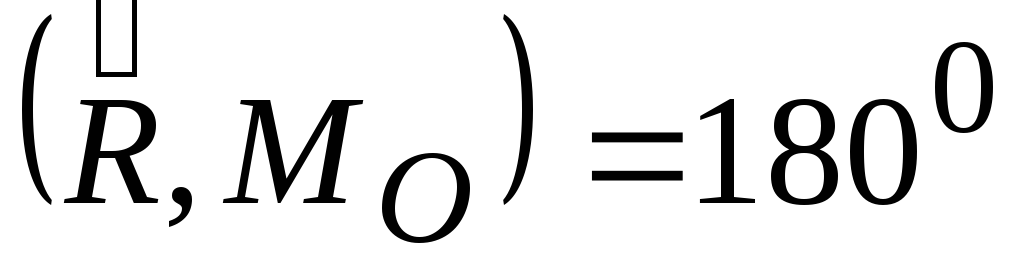, т.е. эти вектора коллинеарные, то такая система называетсядинамическим винтом.

Покажем, что если угол , то систему всегда можно привести к динамическому винту. Рассмотрим такой случай (рис. 38,а). Разложим на две взаимоперпендикулярные составляющие: , которая направлена, перпендикулярна плоскости , и , которая лежит в плоскости .

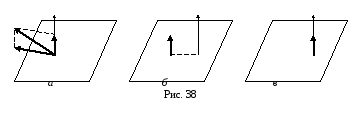
Заменяя вектора и по процедуре, описанной в п. 2, получаем вектор , но проходящий не через точку, а точку(рис. 38,б). Вектор можно свободно переносить в плоскости , используя свойства пар сил. Поэтому переносим параллельно самому себе в точку . В результате получаем два коллинеарных вектора и , которые и образуют динамический винт (рис. 38,в).

4. Приведение к равновесию. Если для данной системы сил и , то она находится вравновесии.

,

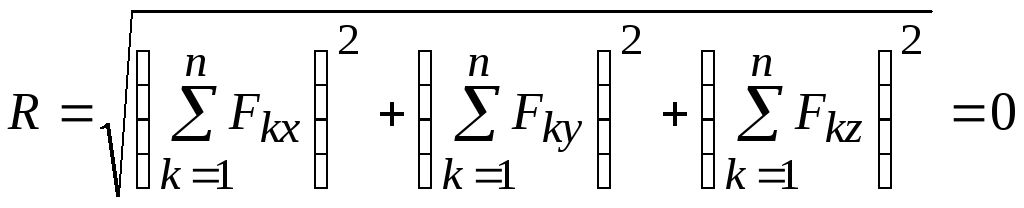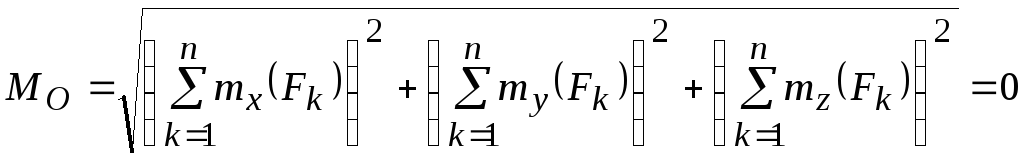
36

, , ,

(10)

, , .

Получили шесть условий равновесия: для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы

проекций всех сил на каждую из координатных осей а также суммы моментов этих сил относительно каждой из координатных осей были равны нулю.