Глава 2.Булева алгебра

2.1. Основные определения

Одна и та же логическая функция может быть задана формулами, включающими различные наборы логических операций. Существуют наборы логических операций (унарных и бинарных), с помощью которых можно выразить любые другие логические функции. Такие наборы называютсяфункционально полными системами(подробнее они будут рассмотрены в п.2.5).

Наиболее хорошо изученной является система булевых функций .Формулы, содержащие кроме переменных (и скобок) только знаки функций , называютсябулевыми.

Алгебра, основным множеством которой является все множество логических функций, а операциями – дизъюнкция, конъюнкция и отрицание, называется булевой алгеброй логических функций.

Элементами основного множества булевой алгебры объявляются не формулы, а классы эквивалентности формул, т.е. классы формул, представляющих одну и ту же функцию (так как фактически мы имеем дело не с самими функциями в чистом виде, а с представляющими их формулами, которых гораздо больше, чем функций).

Теорема 1. Всякая представленная формулой логическая функция может быть представлена булевой формулой, т.е. как суперпозиция функций,,^.

Для доказательства этой теоремы достаточно предложить любой способ построения булевой формулы. Пусть логическая функция задана некоторой формулой F(не являющейся булевой), тогда с помощью эквивалентных преобразований (используя эквивалентные соотношения 1…13) нужно заменить все логические операции на булевы операции.

Очевидно, что булевых формул для каждой логической функции бесконечно много, так как любое эквивалентное преобразование дает новую формулу той же логической функции.

Пример 24. Используя эквивалентные преобразования, получить булеву формулу для функции

.





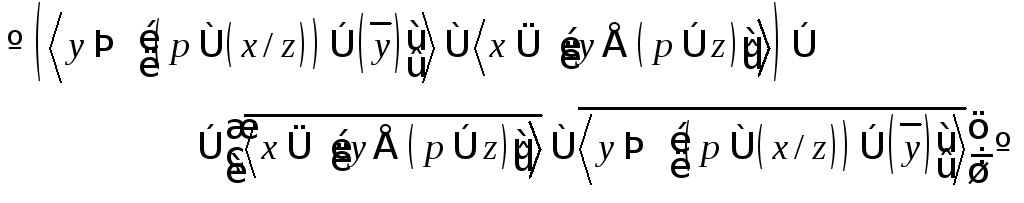
Каждая булева функция имеет конечное число вхождений переменных. Под числом вхождений переменной (длинной) понимается число раз, которое она встречается в алгебраическом выражении этой функции с отрицанием или без.Задача минимизации булевых функцийзаключается в том, чтобы получить алгебраическое выражение булевой функции с наименьшим числом вхождений переменных.

Конъюнкция любого числа переменных, взятых по одному разу, с отрицанием или без отрицания, называется элементарным произведением.

Например,– элементарное произведение,– не является элементарным произведением.

Дизъюнктивной нормальной формой (ДНФ) функции называется такая дизъюнкция нескольких различных элементарных произведений, что таблица истинности ДНФ совпадает с таблицей истинности самой функции. ДНФ может состоять из одного элементарного произведения.

Эквивалентные соотношения в булевой алгебре

Аксиомы конъюнкции	Аксиомы дизъюнкции			Название аксиомы
	xy=yx			коммутативность
	x(yz)=(xy)z			ассоциативность
	xx=x			идемпотентность
				дистрибутивность
				поглощение
	x1=1 x0=x			аксиомы 1и0
				законы де Моргана
аксиома «противоречия»:	аксиома «исключенного третьего»:
Аксиомы отрицания

Пример 25.Получить ДНФ для функции

.

В предыдущем примере мы уже получили булеву формулу для этой функции, поэтому возьмем полученную формулу в качестве исходной и воспользуемся эквивалентными преобразованиями булевой алгебры.

. 

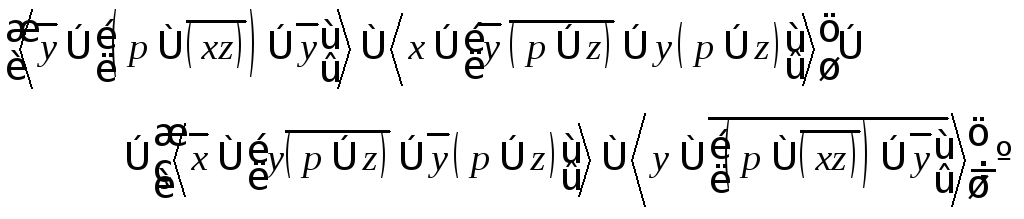
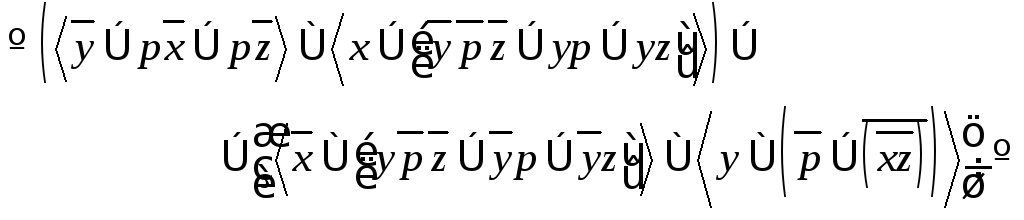
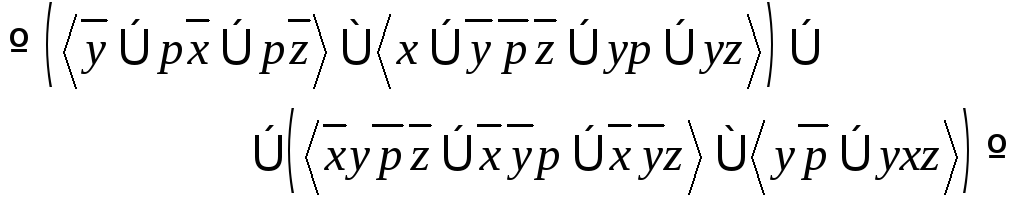
Рассмотрим способ построения булевой формулы для таблично заданной функции.

Обозначим . Очевидно, что.

Конституентой единицы (K¹) данного набора (₁,₂,...,_n) называется конъюнкция всех переменных, образующих этот набор:

,

т.е. если переменная в наборе принимает значение 1, то в конъюнкцию она берется без отрицания, если же в наборе значение переменной 0, то она записывается с отрицанием.

На произвольном фиксированном наборе x₁=₁,x₂=₂, ... ,x_n=_nимеем для конституенты единицы данного набора

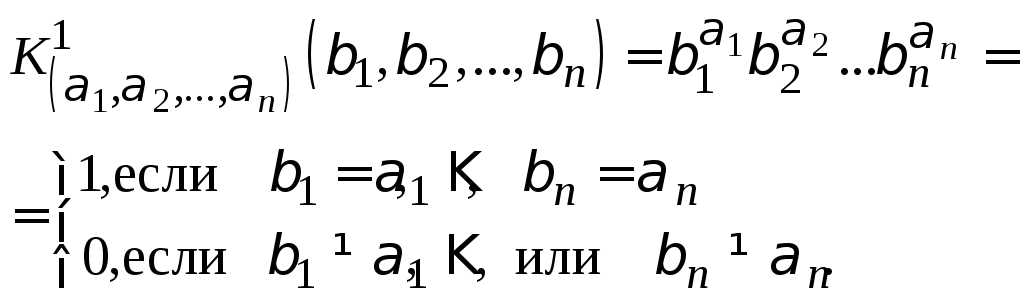
Очевидно, что если , то(так как, если хотя бы один элемент конъюнкции равен 0, то и вся конъюнкция равна 0). Следовательно, верна следующая лемма.

Лемма 1. Конституента единицы равна 1 только на одном наборе.

Конституентой нуля (K⁰) данного набора (₁,₂,...,_n) называется дизъюнкция всех переменных, образующих этот набор:

т.е. если переменная в наборе принимает значение 0, то в дизъюнкцию она берется без отрицания, если же в наборе значение переменной 1, то она записывается с отрицанием.

На произвольном фиксированном наборе x₁=₁,x₂=₂, ... ,x_n=_nимеем для конституенты нуля данного набора:

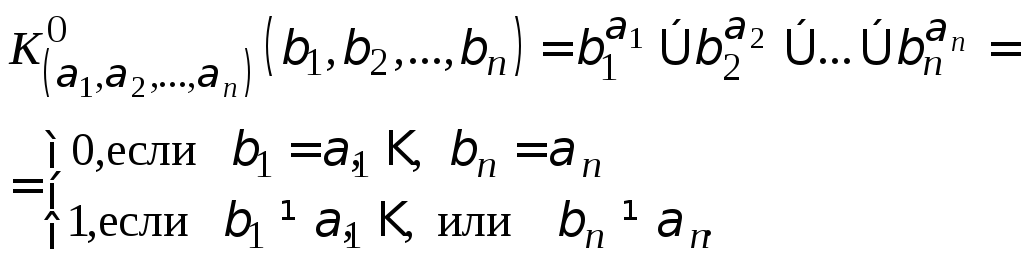
Очевидно, что если , то(так как, если хотя бы один элемент дизъюнкции равен 1, то и вся дизъюнкция равна 1). Следовательно, верна следующая лемма:

Лемма 2. Конституента нуля равна 0 только на «своем» наборе.

СДНФ есть дизъюнкция конституент единицы тех наборов, где функция равна единице:

.

Лемма 3. Всякая переключательная функция, не равная тождественно 0, представима и притом однозначно в совершенной дизъюнктивной нормальной форме (СДНФ).

СКНФ есть конъюнкция конституент нуля тех наборов, где функция равна нулю:

.

Лемма 4. Всякая переключательная функция, не равная тождественно 1, представима и притом однозначно в совершенной конъюнктивной нормальной форме (СКНФ).

Формулы, получаемые перестановкой конъюнкт и дизъюнкт, считаются одной и той же СДНФ (СКНФ) (ввиду коммутативности дизъюнкции и конъюнкции).

Пример 26.Построить таблицу истинности для функцииf, заданной формулой

.

По таблице истинности выписать СДНФ и СКНФ.

Порядок операций:

.

Таблица 3.

Таблица истинности для функции f

	I	II	III	IV	V	VI	VII	VIII	F
x y z p		pI		IIIII	yIV	pz	yVI	xVII	VVIII
0 0 0 0	1	0	1	1	1	0	0	1	1
0 0 0 1	1	1	1	1	1	1	1	0	0
0 0 1 0	1	0	1	1	1	1	1	0	0
0 0 1 1	1	1	1	1	1	1	1	0	0
0 1 0 0	1	0	0	0	0	0	1	0	1
0 1 0 1	1	1	0	1	1	1	0	1	1
0 1 1 0	1	0	0	0	0	1	0	1	0
0 1 1 1	1	1	0	1	1	1	0	1	1
1 0 0 0	1	0	1	1	1	0	0	1	1
1 0 0 1	1	1	1	1	1	1	1	1	1
1 0 1 0	1	0	1	1	1	1	1	1	1
1 0 1 1	0	0	1	1	1	1	1	1	1
1 1 0 0	1	0	0	0	0	0	1	1	0
1 1 0 1	1	1	0	1	1	1	0	1	1
1 1 1 0	1	0	0	0	0	1	0	1	0
1 1 1 1	0	0	0	0	0	1	0	1	0

,

.