§5. Свободные колебания ограниченной струны. Метод отражений (метод продолжений)

Задача о свободных колебаниях ограниченной струны возникает, если оба конца струны находятся достаточно близко от рассматриваемого участка и влияют на его движение. В этом случае колебания описываются функцией , у которойи. Уравнение свободных колебаний (3) должно быть теперь дополнено ГУ на обоих концах и НУ, заданными на. В результате возникает НКЗ

,

(33)

(или )

(34)

Возможен также смешанный случай, когда на одном конце выполняется ГУ I рода, а на другом – II. Краевые условия III рода мы не рассматриваем.

Ход наших рассуждений будет таким же, как в предыдущем параграфе. Рассмотрим сначала случай однородных ГУ, т.е. струну с закрепленными или свободными концами:

(35)

и решим задачу (3), (34), (35). Общее решение уравнения (3) описывается формулой Даламбера (18): , где

, .

Исходно функции g₁ и g₂ определены только при . Наша задача – продолжитьg₁ и g₂ (или и) с промежутка [0,l] на всю вещественную ось, т.е. определить такое начальное возмущение бесконечной струны, при котором ее кусок [0, l] будет колебаться так, как если бы его концы были закреплены (свободны), а остальная часть струны отброшена.

Подставим (18) в ГУ (35):

ГУ I рода: ;

ГУ II рода: ;

(постоянная интегрирования здесь опущена, так как потом при сложении она сокращается). Дальше рассматриваем ГУ I и II рода параллельно (верхний знак соответствует I роду, нижний – II). Обозначим ct = x, тогда

и .

Последние два равенства позволяют однозначно продолжить g₁ и g₂ с [0,l] на всю вещественную ось. При их правые части определены и, значит, определеныg₁ при иg₂ при . Теперь правые части тех же равенств определены при, что задаетg₁ при иg₂ при . Продолжая эту процедуру, определимg₁ при иg₂ при . Рассмотрим теперь те же равенства при; их левые части определены и, следовательно, определеныg₁ при иg₂ при . Дальнейшее повторение этой процедуры однозначно задаетg₁ при иg₂ при . Таким образом, функцииg₁ и g₂ оказались определенными на всей вещественной оси, при этом

,

т.е. обе функции периодичны с периодом 2l.

Обратимся к начальным данным Коши и; для них:

;

Кроме того, из периодичности g₁ и g₂ следует, что итакже периодичны с периодом 2l. Таким образом, при однородных ГУ I рода (II рода) начальные данные Коши должны быть продолжены с напо закону нечетности (четности) и дальше с периодом 2l на всю вещественную ось.

Наши построения показывают, что однородная НКЗ для ограниченной струны (3), (34), (35) эквивалентна задаче Коши для бесконечной струны:

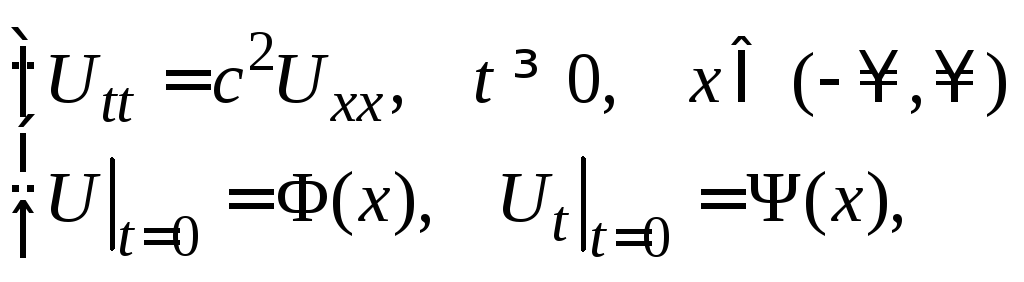
где

здесь k- целое число; аналогично определяется через. Решение исходной НКЗ совпадает с решением задачи Коши на промежутке:

Функция U(x,t) определяется формулой Даламбера:

. (36)

Упражнение 9. Проверить прямой выкладкой, что функция U(x,t) при x = 0, x = l удовлетворяет ГУ (35).

Замечание. Если функции итаковы, чтоимеет две иодну непрерывные производные на всей оси, формула (36) дает классическое решение задачи (3, 34, 35), т.е. имеет место теорема существования. Теорема единственности следует из наших рассуждений, если проводить их строго. Устойчивость этой задачи также имеет место, на ее доказательстве мы не останавливаемся.

Физическая интерпретация решения. Отметим на оси x точки вида kl, где k - целое число, и проведем через них характеристики (рис. 9). Область I соответствует точкам струны, до которых в данный момент дошло возмущение только от исходных точек, т.е. фиктивно добавленные бесконечные части на их движение не влияют. В III приходит возмущение от исходной струны и обратная волна от фиктивного куска . Эта обратная волна задается функцией, причем точка (x,t) принадлежит области III. Для области III , поэтому

.

Видно, что обратная волна от фиктивной точки есть с точностью до знака прямая волна от реальной точки, симметричной относительно концаx = l. Прямая волна g₁ из точки в моментдошла до конца струны, отразилась (изменила свое направление) и в моментt пришла в точку .

Итак, в III есть волна от исходного возмущения и прямая волна, отразившаяся от конца x = l. В II есть волна от исходного возмущения и обратная волна, отразившаяся от конца x = 0. Следующие области соответствуют точкам, в которых в данный момент накладываются многократно отраженные волны.

Действие закрепленного (свободного) конца x = 0 или x = l приводит к отражению волны смещения от этого конца, связанному с изменением направления распространения волны на противоположное, с сохранением абсолютной величины смещения и переменой (сохранением) знака смещения.

Влияние граничного режима. При рассмотрении неоднородных ГУ ограничимся условиями I рода, т.е. будем предполагать, что концы струны движутся по известным законам. Решение задачи (3), (33), (34) следует искать в виде суммы

где - решениеI НКЗ с однородными ГУ (3, 35, 34), а функции иудовлетворяют НКЗ с нулевыми данными Коши:

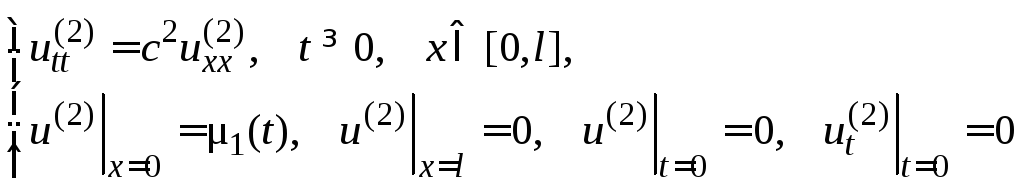(37)

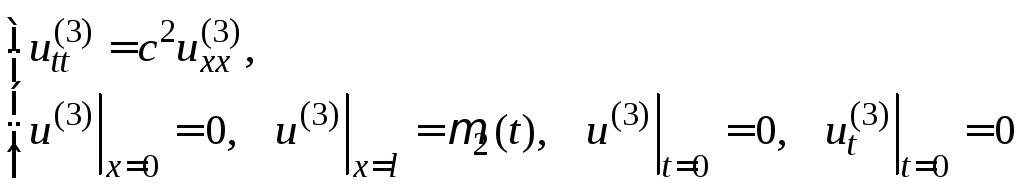
Задачу (37) будем решать так же, как (29) в предыдущем параграфе. Построенное там решение

, где

удовлетворяет (37) при . Когдаt достигает , нарушается ГУ на правом конце.

Пусть , волна, бегущая налево и колеблющаяся в точкепо закону, описывается функцией. Разность двух волндает решение задачи (37) при. Продолжая это рассуждение, получим для любогоt решение задачи (37) в виде ряда

(38)

При любом фиксированном t сумма (38) содержит конечное число слагаемых. Физически решение (38) означает, что граничный режим создает волну, которая последовательно отражается от обоих концов; решение есть суперпозиция отраженных волн.

Аналогичные рассуждения позволяют построить для функции , удовлетворяющей НКЗ с неоднородным ГУ на правом конце отрезка, ряд

; (39)

здесь функция определяется черезаналогично.

Упражнение 10. Проверить прямой выкладкой, что функции иудовлетворяют поставленным НКЗ.