
А) Разложение экспоненты
Для
всех
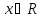 имеет место равенство
имеет место равенство
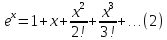
Для доказательства равенства (2) убеждаемся, что
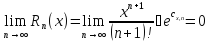
при
любом фиксированном
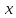 и любых величинах
и любых величинах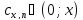 .
Далее применяем предложение предыдущего
параграфа. По другому докажем равенство
(2):как функция
.
Далее применяем предложение предыдущего
параграфа. По другому докажем равенство
(2):как функция
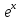 ,
так и сумма
ряда в (2) - решения дифференциального
уравнения
,
так и сумма
ряда в (2) - решения дифференциального
уравнения
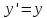 с начальным условием y(0)=1. Из теоремы
единственности решения дифференциального
уравнения следует, что в этом случае
функции совпадают.
с начальным условием y(0)=1. Из теоремы
единственности решения дифференциального
уравнения следует, что в этом случае
функции совпадают.
Б) Разложение гармоник
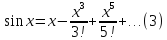
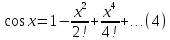
Равенства
(3) и (4) можно доказать так же как и для
экспоненты, доказав, что остаток в
разложении по формуле Маклорена
стремится к нулю при
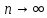 .
По другому, можно рассуждать так:
рассмотрим
дифференциальное уравнение
.
По другому, можно рассуждать так:
рассмотрим
дифференциальное уравнение
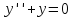 с начальными условиями y(0)=0, y'(0)=1 для
функции sin x и y(0)=1, y'(0)=0 для функции cos x.
Тогда ряды (3) и (4) также как и функции
с начальными условиями y(0)=0, y'(0)=1 для
функции sin x и y(0)=1, y'(0)=0 для функции cos x.
Тогда ряды (3) и (4) также как и функции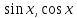 -- решения этого диф. уравнения с
указанными начальными условиями. По
теореме единственности решения диф.
уравнения с заданными начальными
условиями, получаем совпадение гармоник
с рядами (3) и (4).
Можно поступить и иначе: подставить в
разложение (2) вместо
-- решения этого диф. уравнения с
указанными начальными условиями. По
теореме единственности решения диф.
уравнения с заданными начальными
условиями, получаем совпадение гармоник
с рядами (3) и (4).
Можно поступить и иначе: подставить в
разложение (2) вместо
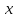 чисто мнимое число
чисто мнимое число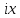 ,
а далее приравнять действительные и
мнимые части - получим в точности (3) и
(4).
,
а далее приравнять действительные и
мнимые части - получим в точности (3) и
(4).
Заметим, что во всех трех равенствах (2),(3),(4) радиус сходимости ряда, стоящего справа равен бесконечности, т.е. разложения имеют место на всей числовой оси.
???Приближенные вычисления, вычисления определенных интегралов и решения дифференциальных уравнений с помощью рядов.
Вычислим
интеграл
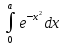 :
:
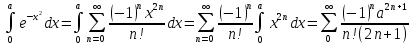
Решим
дифференциальное уравнение
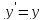 c
начальным условием
c
начальным условием
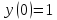 .
Полагая
.
Полагая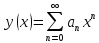 и подставляя этот ряд в дифференциальное
уравнение, а затем почленно интегрируя,
а затем приравнивая коэффициенты при
одинаковых степенях, получим
и подставляя этот ряд в дифференциальное
уравнение, а затем почленно интегрируя,
а затем приравнивая коэффициенты при
одинаковых степенях, получим
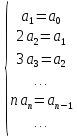
Так
как
 ,
то последовательно находим коэффициенты
,
то последовательно находим коэффициенты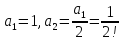 ,
,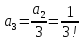 и т.д.
и т.д.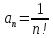 .
Получаем
.
Получаем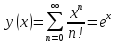 .
Полученный ряд имеет бесконечный радиус
сходимости. Это оправдывает операцию
почленного дифференцирования при любом
.
Полученный ряд имеет бесконечный радиус
сходимости. Это оправдывает операцию
почленного дифференцирования при любом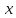 .
.
Общие понятия (определение дифференциального уравнения, решения, порядка, нормальной формы записи). Дифференциальные уравнения 1-го порядка, задача Коши, теорема существования и единственности.
Дифференциа́льное уравне́ние — уравнение, связывающее значение производной функции с самой функцией, значениями независимой переменной, числами (параметрами).
В этом разделе мы будем решать уравнения, неизвестным в которых ответом является функция. В разделе «Неопределенный интеграл» мы фактически занимались решением уравнения
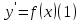
Требовалось найти
такую функцию-первообразную
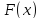 ,
производная которой тождественно равна
,
производная которой тождественно равна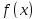 .
Решений у уравнения (1) бесконечно много,
и все они отличаются друг от друга на
константу. Эту множественность решений
можно обозревать и с другой точки
зрения. Фиксируем значение первообразной
в определенной точке:
.
Решений у уравнения (1) бесконечно много,
и все они отличаются друг от друга на
константу. Эту множественность решений
можно обозревать и с другой точки
зрения. Фиксируем значение первообразной
в определенной точке:
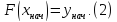
Считаем
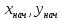 начальными условиями. Тогда для
непрерывной функции
начальными условиями. Тогда для
непрерывной функции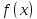 ,
заданной на интервале
,
заданной на интервале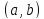 и начальных условий
и начальных условий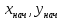 c
условием
c
условием
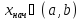 существует и единственно решение
существует и единственно решение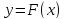 уравнения (1), удовлетворяющее соотношению
(2). Более того, ответ задается формулой
уравнения (1), удовлетворяющее соотношению
(2). Более того, ответ задается формулой
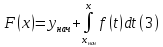
Сформулирована теорема существования и единственности для дифференциального уравнения самого простого вида. Рассмотрим теперь уравнение вида
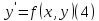
Его полное название
– обыкновенное дифференциальное
уравнение первого порядка в нормальной
форме. Обыкновенное, так как неизвестная
функция
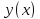 зависит лишь от одной переменной, в
отличии, например, от уравнения Лапласа
зависит лишь от одной переменной, в
отличии, например, от уравнения Лапласа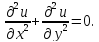 Первого порядка – так как старшая
производная, входящая в уравнение (4)
имеет первый порядок. Нормальная форма
записи дифференциального уравнения
означает, что старшая производная
выражена через младшие производные, а
также саму неизвестную функцию, а также
переменную. Таким образом,
Первого порядка – так как старшая
производная, входящая в уравнение (4)
имеет первый порядок. Нормальная форма
записи дифференциального уравнения
означает, что старшая производная
выражена через младшие производные, а
также саму неизвестную функцию, а также
переменную. Таким образом,
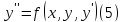
есть дифференциальное уравнение второго порядка в нормальной форме, а
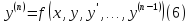
есть общий вид
дифференциального уравнения n-го
порядка в нормальной форме. Решение
уравнений вида (4) составляет основную
задачу данной темы. При этом функция
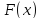 называется (частным) решением уравнения
(4) или (6), если при подстановки вместо
называется (частным) решением уравнения
(4) или (6), если при подстановки вместо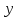 в это уравнение получаем тождество.
в это уравнение получаем тождество.
Задача решения
дифференциального уравнения с заданными
начальными условиями называется задачей
Коши. Начальные условия для уравнения
(6) задаются рядом чисел
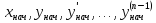 и выглядят так
и выглядят так
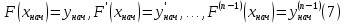
Теорема
существования и единственности.
Если в дифференциальном уравнении
первого порядка(4) функция
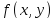 вместе со своей частной производной
вместе со своей частной производной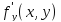 непрерывны в области, содержащей
непрерывны в области, содержащей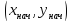 как свою внутреннюю точку, то найдется
интервал
как свою внутреннюю точку, то найдется
интервал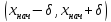 для которого, существует и единственно
решение
для которого, существует и единственно
решение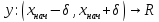 задачи Коши.
задачи Коши.
Общая теорема
для уравнения n-го
порядка (6) гласит, что если функция
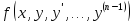 вместе со всеми своими частными
производными по второй, третьей и т.д.
поn-ой
переменной непрерывны в пространственной
области
вместе со всеми своими частными
производными по второй, третьей и т.д.
поn-ой
переменной непрерывны в пространственной
области
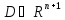 ,
содержащей точку
,
содержащей точку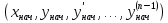 ,
то локальное решение задачи Коши
существует и единственно.
,
то локальное решение задачи Коши
существует и единственно.
Дифференциальные уравнения 1-го порядка с разделяющимися переменными. Однородные дифференциальные уравнения первого порядка.
