
3.8. Интегральная теорема Муавра-Лапласа
В рассмотренном выше примере вероятность получилась довольно малой, несмотря на то, что вероятность появления стандартной детали равна 0,9. Это объясняется тем, что была вычислена вероятность только одного из 401 исходов. Поэтому в практических приложениях представляет интерес вычисления не одного, а нескольких исходов. Такую вероятность можно получить путем суммирования по всем возможным исходам m. Однако при больших n и достаточно широких пределов изменения величины m вычисления будут довольно громоздкими. В этих случаях для приближенных вычислений используется
Интегральная теорема Муавра-Лапласа. Если в схеме Бернулли число испытаний n велико, то для вероятности Pn(k1mk2) того, что число успехов заключено в пределах от k1 до k2, справедливо приближенная формула
![]() ,
(3.15)
,
(3.15)
где
![]() ,
,![]() –функция
Лапласа.
–функция
Лапласа.
Отметим, что функция Лапласа – нечетная функция, т.е. Ф(–x) = –Ф(x), для которой составлены специальные таблицы. Обратите внимание, что 0Ф(x)0,5.
Доказательство теоремы проведем, опираясь на локальную теорему Муавра-Лапласа (здесь мы также опускаем отдельные технические детали доказательства). Очевидно, что вероятность Pn(k1mk2) можно представить в виде
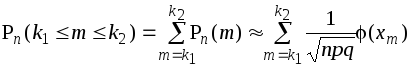 .
.
Так как
![]() ,
,
то сумму можно написать в виде
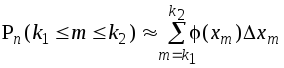 ,
,
которая
мало чем отличается от подходящим
образом выбранной интегральной суммы,
соответствующей интегралу
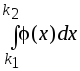 .
Следовательно,
.
Следовательно,
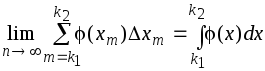 .
.
Таким образом,
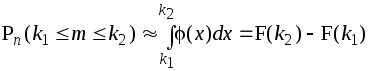 ,
,
где
![]() –функция
стандартного нормального распределения.
Часто вместо функции F(x)
используется
функция Лапласа Ф(x)=F(x)–0,5.
Отметим
еще, что в некоторых учебниках за функцию
Лапласа принимают вдвое большую функцию
–функция
стандартного нормального распределения.
Часто вместо функции F(x)
используется
функция Лапласа Ф(x)=F(x)–0,5.
Отметим
еще, что в некоторых учебниках за функцию
Лапласа принимают вдвое большую функцию
![]() = 2Ф(x);
в этом
случае 0
= 2Ф(x);
в этом
случае 0![]() 1.
1.
Пример 3.16. В среднем в ОТК бракуется 10% изделий. На контроль отобрано 625 изделий. Какова вероятность того, что среди них не менее 550 и не более 575 стандартных изделий?
Решение. По условию задачи n=625, p=0,9, q=0,1, k1=550, k2=575. Поскольку npq=56,25»1 и n=625>100, то искомую вероятность найдем при помощи интегральной формулы Муавра-Лапласа:
![]() ,
,
![]() ,
,
![]()
= 2·0,45221 = 0,90442.
Более точные компьютерные вычисления, с использованием формулы Бернулли, дают следующий результат P625(550m575) = 0,90431. Видно, что использование интегральной теоремы Муавра-Лапласа было вполне оправданным.
3.9. Теорема Пуассона
При использовании теорем Муавра-Лапласа можно заметить, что она действует тем "хуже", чем больше вероятность p отличается от 1/2, т.е. чем ближе вероятность к 1 или 0. Однако значительное число задач связано с необходимостью вычисления вероятностей Pn(m) именно при малых значениях p (или q).
Теорема Пуассона. Если в схеме Бернулли число испытаний n велико, а вероятность успеха p в одном испытании мала, причем мало также произведение np, то справедлива приближенная формула
![]() ,
(3.16)
,
(3.16)
где = np.
Доказательство. Запишем формулу Бернулли
![]()
или, с учетом обозначения = np, p = /n:
![]() .
.
Известно, что
![]() .
.
Кроме
того, если n
велико, то
![]() ,
,![]() ,
...,
,
...,![]() и
и![]() .
Поэтому
.
Поэтому
![]() ,
,
что и требовалось доказать.
Отметим, что формула Пуассона справедлива также по отношению к числу неудач, но только в том случае, когда мало = nq.
Теперь рассмотрим некоторые рекомендации по применению приближенной формулы Пуассона. 1) Если число испытаний n=1020, то теорема Пуассона используется для грубых оценок, когда = np или = nq изменяются в пределах от 02 (при n=10) до 03 (при n=20); в противном случае необходимо пользоваться формулами Муавра-Лапласа. 2) Если n=20100, то формулу Пуассона рекомендуется применять, когда и заключаются в следующих пределах: от 03 (при n=20) до 05 (при n=100). 3) Если n=1001000, то формула Пуассона используется, когда и изменяются в следующих пределах: от 05 (при n=100) до 010 (при n=1000). 4) Если n>1000, то необходимо чтобы и лежали в пределах 010 и более.
Еще раз отметим, что приближенные формулы Пуассона и Муавра-Лапласа гарантируют только малую абсолютную погрешность, но не относительную погрешность.
Пример 3.17. Счетчик Гейгера регистрирует попадание в него -частицы с вероятностью p=0,9. Найти вероятность того, что он зарегистрировал m (m=0,1,2,...,10) частиц при условии, что в него попало n=10 частиц.
Решение. Воспользуемся сначала точной формулой Бернулли, в соответствии с которой
![]() .
.
После этого воспользуемся приближенной формулой Пуассона. В данном случае = np =9 – велико, а = nq = 1 мало. Это значит, что нужно воспользоваться формулой Пуассона, но по отношению к незарегистрированным частицам. В соответствии с этой формулой
![]() .
.
Результаты вычислений P10(m) занесем в таблицу.
|
m |
Точное значение, формула Бернулли |
Приближенное значение, формула Пуассона |
Абсолютная погрешность |
Относительная погрешность % |
|
0 |
0 |
0 |
- |
- |
|
1 |
0 |
0,000001 |
0,000001 |
- |
|
2 |
0 |
0,000009 |
0,000010 |
- |
|
3 |
0,000009 |
0,000073 |
0,000064 |
734 |
|
4 |
0,000138 |
0,000511 |
0,000373 |
271 |
|
5 |
0,001488 |
0,003066 |
0,001578 |
106 |
|
6 |
0,011160 |
0,015328 |
0,004168 |
37,4 |
|
7 |
0,057396 |
0,061313 |
0,003918 |
6,8 |
|
8 |
0,193710 |
0183940 |
–0,009771 |
5,0 |
|
9 |
0,387420 |
0,367879 |
–0,019541 |
5,0 |
|
10 |
0,344678 |
0,367879 |
0,019201 |
5,5 |
Анализируя приведенные результаты, видно, что максимальная абсолютная погрешность невелика, чего нельзя сказать о максимальной относительной погрешности. Если в данной задаче воспользоваться локальной теоремой Муавра-Лапласа (чего не рекомендуется делать, поскольку npq=0,9 сравнимо и даже меньше единицы), то получим результаты, имеющие существенно большие погрешности.
Пример 3.18. Радиоаппаратура состоит из 900 элементов. Вероятность отказа одного элемента в течение года работы равна p=0,001 и не зависит от состояния других элементов. Какова вероятность отказа не менее двух элементов за год?
Решение. Поскольку =np=0,9, то можно применить теорему Пуассона. Тогда
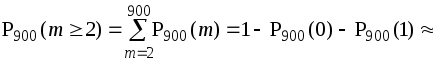
![]() .
.
Точное значение
![]()
практически не значительно отличается от приближенного. Следовательно, в данной задаче допустимо применение формулы Пуассона.
