S&M

Содержание

1Элементы математической статистики . . . . . . . . . . . . . . . 4

1.1Первичная обработка данных . . . . . . . . . . . . . . . . 4

1.2Вычисление оценок числовых характеристик статистического распределения . . . . . . . . . . . . . . . . . . . . 7

1.3Выравнивание статистического ряда . . . . . . . . . . . . 8

1.4Статистическая проверка гипотез. Критерий согласия . . 10 Литература . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14

Приложения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15

3

1Элементы математической статистики

Основной задачей математической статистики является описание и анализ экспериментальных данных, полученных в результате наблюдения массовых случайных явлений. В статистике множество значений, которые может принимать исследуемая случайная величина (в дальнейшем С.В.) X, называется генеральной совокупностью. Подмножество, отобранное из генеральной совокупности случайным образом (наугад), называется случайной выборкой или простой статистической совокупностью. Элементы случайной выборки обозначаются буквами x1; x2; : : : ; xn, где n - объем выборки.

Задача методов математической статистики состоит в том, чтобы по выборке, извлекая из нее максимум информации, сделать те или иные выводы о генеральной совокупности, в частности, выводы о параметрах распределения С.В. и правдоподобии гипотезы о том, что С.В. имеет тот или иной закон распределения.

1.1Первичная обработка данных

Выборка из генеральной совокупности представляет собой первичный статистический материал, подлежащий обработке и анализу. Если объем выборки достаточно велик (порядка сотен), то для придания статистическому материалу большей компактности и наглядности его подвергают дополнительной обработке, а именно: строят статистический ряд.

Для этого весь диапазон наблюдаемых значений С.В. X делят на интервалы (так называемые "разряды") и подсчитывают количество значений С.В., попавших в данный разряд. Эти величины называют частотами, их обознача-

ют mi (т.е. mi – это частота i-го разряда [xi¡1; xi]). Очевидно, что Pk mi = n,

i=1

где n - объем выборки, k – число разрядов.

Замечание 1. Количество разрядов k при заданном объеме выборки n обычно определяют из соотношения: k ¸ 3; 32 lg n + 1. Так, например, при n = 100 получим k ¸ 8.

Замечание 2. В случае, если значение С.В. находится на границе двух разрядов, то, по договоренности, его относят либо к "левому", либо к "правому" разряду, либо к частотам обоих смежных разрядов добавляют по

1=2.

Далее числа mi делят на общее число наблюдений n и находят относи-

тельные частоты или частости разрядов Wi = mi n

4

Очевидно, что Pk Wi = 1.

i=1

Таблица, в которой приведены разряды в порядке их расположения вдоль оси абсцисс и соответствующие им частоты и частости, называется упорядоченным вариационным рядом.

Статистический ряд оформляется графически в виде гистограммы, которая строится следующим образом. По оси абсцисс откладывают разряды и на каждом из них строят прямоугольник, площадь которого равна относительной частоте или частости данного разряда. Из способа построения гистограммы следует, что высота каждого прямоугольника hi = ¢Wxi (здесь ¢x¡ длина разряда). Полная площадь гистограммы равна единице.

Пример 1.

Случайная величина X, представляющая собой ошибку измерения некоторого расстояния, задана простой статистической совокупностью (Таблица1). Составить упорядоченный вариационный ряд и построить гистограмму частостей, заполнив Таблицу 2.

Таблица 1.

Простая статистическая совокупность

5

1)Определим размах выборки R. Для этого найдем наименьшее и наибольшее значения С.В. X:

xmin = x7 = 111; xmax = x25 = 296

и вычислим размах R = xmax ¡ xmin = 296 ¡ 111 = 185.

2)Выберем число разрядов k = 10.

3)Примем за интервал задания С.В. X такой промежуток, который содер-

жит xmin, xmax и имеет достаточно близкие к ним границы со значениями, более удобными для расчетов: x0 = 100, x10 = 300.

4)Построим упорядоченный вариационный ряд. Для этого найдем длину разряда и заполним Таблицу 2. Для контроля расчета найдем столбцовые суммы.

5)По результатам, полученным в Таблице 2, построим гистограмму. Для этого в прямоугольной системе координат на оси абсцисс отложим значения границ разрядов и на каждом из интервалов с номером i построим прямоугольник высоты hi (рис. 1).

6

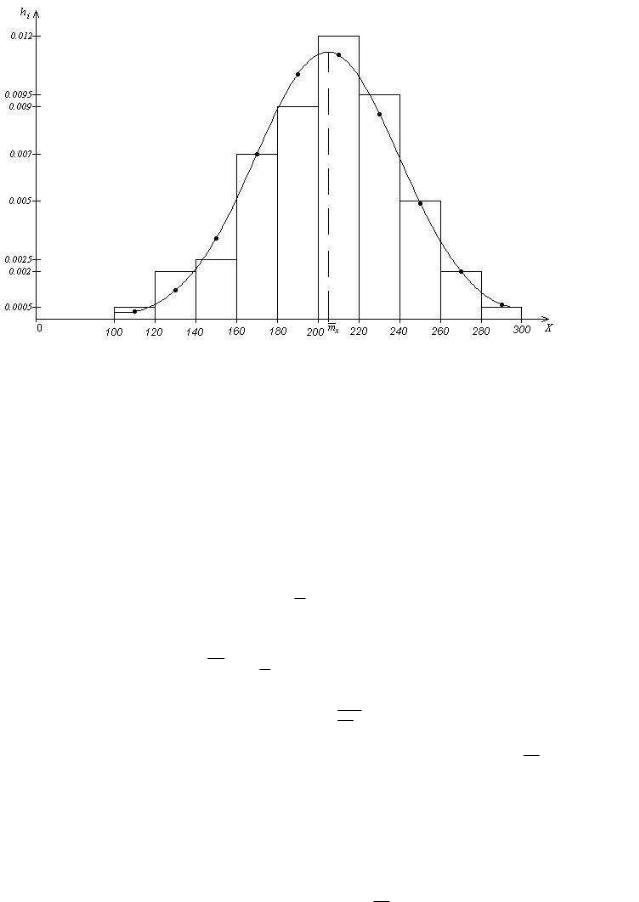
Рис. 1.

1.2Вычисление оценок числовых характеристик статистического распределения

При большом количестве опытов статистические значения числовых характеристик С.В. вычисляют по формулам:

1 Xk

mx = n i=1 xi ¢ mi;

Dx = n1 Xk (xi ¡ mx)2 ¢ mi; i=1 q

¾x = Dx;

где mx– статистическое значение математического ожидания, Dx– статистическое значение дисперсии, ¾x– статистическое значение среднеквадратичного отклонения.

Пример 2.

Для cлучайной величины X из примера 1 найти числовые характеристики математического ожидания mx и дисперсии Dx.

7

1 X10

mx = 100 i=1 xi ¢ mi;

1 X10

Dx = 100 i=1 (xi ¡ mx)2 ¢ mi:

Для удобства вычисления численных значений характеристик заполним Таблицу 3.

Таблица 3.

Вычисление статистических значений числовых характеристик С.В.

1.3Выравнивание статистического ряда

При обработке статистического материала одним из важнейших вопросов является вопрос о том, как подобрать для данного статистического ряда теоретическую кривую распределения, выражающую только существенные черты статистического материала, а не случайности, связанные с недостаточным объемом экспериментальных данных. Такая задача называется задачей выравнивания (сглаживания) статистических рядов.

8

Таким образом, задача выравнивания состоит в том, чтобы подобрать теоретическую плавную кривую распределения, наилучшим образом описывающую данное статистическое распределение.

Пример 3.

Вернемся к примеру 1. Так как случайная величина X есть ошибка измерения, возникающая в результате суммирования множества независимых элементарных ошибок, то из теоретических соображений можно предположить, что С.В. X подчиняется нормальному закону. Поэтому выровняем гистограмму теоретическим нормальным законом. Принимая m = mx, D = Dx, ¾ = ¾x, запишем плотность вероятности аппроксимирующего закона:

Для иллюстрации эффективности подбора найдем значения функции f (x) в точках xi (см. Приложение, Таблица 2), нанесем их на рис. 1 и соединим

плавной кривой, учитывая, что вершина кривой имеет координаты

µ 1 ¶ mx; ¾p2¼ .

Результаты расчета занесем в Таблицу 4.

Таблица 4.

Выравнивание статистического закона распределения

9

1.4Статистическая проверка гипотез. Критерий согласия

Предположим, что данное статистическое распределение выровнено с помощью некоторой теоретической кривой f (x). Очевидно, что между статистическим распределением и теоретической кривой неизбежны расхождения. Тогда возникает вопрос о том, насколько эти расхождения существенны и связаны ли они с тем, что подобранная нами кривая плохо выравнивает данное статистическое распределение. Для ответа на этот вопрос применяют "критерий согласия".

Идея применения критериев согласия состоит в том, что на основании известного статистического материала проводится проверка гипотезы о том, что исследуемая С.В. X подчиняется некоторому определенному закону распределения (например, нормальному, показательному и т.д.).

Наиболее часто применяемым критерием согласия является "критерий Â2" Пирсона, суть которого заключается в следующем. Для проверки того, согласуются ли экспериментальные данные с гипотезой о том, что С.В. X имеет данный "теоретический" закон распределения, находят теоретические вероятности попадания случайной величины в каждый из разрядов (они обозна-

чаются pi) и вычисляют величину Â2 = Pk (mi ¡ npi)2 . Значение Â2 зависит

i=1 npi

от параметра r, который называется числом "степеней свободы" и находится как разность числа разрядов k и числа независимых условий ("связей"), наложенных на относительные частоты.

Для Â2 составлены специальные таблицы (см. Приложение, Таблица 3, Таблица 4), из которых по известным значениям Â2 и r находят вероятность p. Если эта вероятность p мала (практически меньше 0; 1), то результат опыта следует считать противоречащим выдвинутой гипотезе, и эта гипотеза отбрасывается, как неправдоподобная. Если же вероятность p сравнительно велика, то можно считать расхождения между статистическим и теоретическим распределениями несущественными и гипотезу о том, что случайная величина подчиняется данному теоретическому закону распределения, можно считать правдоподобной.

Замечание.

Вывод о "правдоподобности" гипотезы ни в коем случае не следует понимать как достоверный факт того, что гипотеза верна. Этот вывод означает только то, что гипотеза не противоречит опытным данным (не более того).

10

Пример 4.

Для рассмотренной в предыдущих примерах случайной величины X рассмотрим гипотезу о том, что она имеет нормальный закон распределения.

Тогда теоретические вероятности того, что С.В. попадает в i-й разряд

0

находят из таблицы (см. Приложение, Таблица 1). Результаты вычислений заносим в Таблицу 5.

Таблица 5.

Далее определим число степеней свободы: r = k ¡ 3 = 10 ¡ 3 = 7, где "3" -

число связей, наложенных при выборе теоретической зависимости, а именно:

Pk Wi = 1; mx = m; Dx = D. i=1

По значениям Â2 и r из таблицы (см. Приложение, Таблица 3) находим искомую вероятность: p ¼ 0; 9.

Так как p > 0; 1, то гипотезу о нормальном законе распределения данной

11

случайной величины можно считать не противоречащей опытным данным, и нормальный закон может быть принят в качестве аппроксимирующего.

Постановка задачи

Случайная величина X, являющаяся ошибкой измерения некоторого расстояния, задана простой статистистической совокупностью (Таблица 1). Необходимо получить упорядоченный вариационный ряд, построить гистограмму частостей, выровнять статистический закон теоретическим (нормальным), проверить соответствие выбора.

Порядок выполнения работы

1.Определить размах вариационного ряда. Для этого выбрать наименьшее

инаибольшее значения случайной величины (т.е. xmin и xmax) и вычислить размах R = xmax ¡ xmin.

2.Выбрать число разрядов k.

3.Принять за интервал задания случайной величины промежуток, который содержит xmin и xmax и имеет границы, достаточно близкие к ним

иявляющиеся более удобными для вычислений.

4.Найти длины разрядов ¢x и заполнить Таблицу 2. Для проверки расчетов найти столбцовые суммы (см. Пример 1).

5.Используя Таблицу 2, построить гистограмму (рис. 1).

6.Заполнить Таблицу 3 и с ее помощью вычислить статистические значения математического ожидания, дисперсии и среднеквадратичного отклонения (см. Пример 2).

7.Выровнять гистограмму теоретическим нормальным законом распределения. Принимая m = mx, ¾ = ¾x, записать плотность вероятности

аппроксимирующего закона

Для иллюстрации эффективности подбора найти значения f (x) в серединных точках интервалов xi, заполнить Таблицу 4, нанести точки на рис. 1, найти вершину кривой и соединить полученные точки плавной линией (см. Пример 3).

12