всюду» (Р-п.в.) или просто «почти наверное» (п.н.), «почти всюду» (п.в.). Используют также термин: свойство выполнено с вероятностью 1.

М4). Если X ≥ 0 п.н. (то есть P(X ≥ 0) =1), то M X ≥ 0.

Если X ≥ 0 п.н. и при этом M X = 0, то X = 0 п.н. (то есть P(X = 0) =1).

▲ Доказательство свойства для дискретных случайных величин очевидно. Для непрерывных случайных величин доказательство следует из того, что плотность вероятностей f (x) = 0 при x < 0 ■.

М5). Если X ≤Y п.н., то M X ≤ MY .

Если X ≤Y п.н. и при этом M X = MY , то X =Y п.н..

▲ Для доказательства достаточно применить свойство М4) к случайной величине Y − X ≥ 0 п.н. ■.

М6). M X ≤ M X

▲ Поскольку − X ≤ X ≤ X для любого ω Ω, то в силу свойства М5) −M X ≤ M X ≤ M X , то есть M X ≤ M X ■.

Замечание. Свойство М6) справедливо и в более общем виде:

Для любой выпуклой вниз функции g = g(x) справедливо неравенство: g(M X ) ≤ M g(X ) (неравенство Йенсена).

Моменты. Дисперсия. Среднее квадратическое отклонение.

Кроме математического ожидания, в теории вероятностей используется еще ряд числовых характеристик различного назначения. Среди них основную роль играют моменты – начальные и центральные.

Определение. Начальным моментом k -го порядка случайной величины

Определение. Центральным моментом k -го порядка случайной величины X называется математическое ожидание k -ой степени отклонения этой случайной величины от ее математического ожидания:

µk = M(X −M X )k , (2.10)

если математическое ожидание существует.

26

момент – это начальный момент для центрированной случайной величины:

µk = M X k .

Аналогично начальным моментам, используются центральные моменты µk , как правило, целого положительного порядка. В частности, при k =1 имеем

µ1 = M X = M(X −M X ) = 0 для всех случайных величин.

Особое значение для практики имеет второй центральный момент µ2 , который называется дисперсией случайной величины и обозначается D X .

Определение. Дисперсией случайной величины X называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

DX = M(X −MX )2 . (2.11)

Для дисперсии DX справедливо также следующее выражение:

DX = M(X −MX )2 = M X 2 −2X M X +(M X )2 =

= M X 2 −2MX M X +(M X )2 = M X 2 −(M X )2

Таким образом, наряду с (2.11), имеем эквивалентное определение дисперсии DX :

D X = M X 2 −(M X )2 . (2.12)

С помощью формулы (2.12) на практике вычислять дисперсию часто бывает проще.

Дисперсия D X характеризует степень разброса (рассеивания) значений случайной величины относительно ее среднего значения (математического ожидания). Чем плотнее группируются значения случайной величины около математического ожидания, тем дисперсия меньше (ср. со смыслом параметра

σ2 в нормальном законе распределения).

Механическая интерпретация дисперсии. Дисперсия представляет собой момент инерции распределения масс относительно центра масс (центра тяжести, математического ожидания).

Вычисляются начальные моменты αk по формулам, вытекающим из основной теоремы о математическом ожидании для функции g (x)= xk :

если Х – дискретная случайная величина, то

αk =MX k = ∑xik pi ;

i

если Х – непрерывная случайная величина, то

αk =MX k = ∞∫ xk f (x)dx .

−∞

27

Центральные моменты µk вычисляются по формулам, вытекающим из основной теоремы о математическом ожидании для функции g (x)=(x −MX )k :

если Х – дискретная случайная величина, то

µk = M(X - M X )k = ∑(xi −M X )k pi ;

i

если Х – непрерывная случайная величина, то

µk = M(X - M X )k = ∞∫(x −M X )k f (x)dx .

−∞

Формулы для вычисления дисперсии DX вытекают из основной теоремы о математическом ожидании для функции g (x)=(x −MX )2 , если используется

D2). Дисперсия не изменяется при прибавлении к случайной величине константы:

D(X +C) = D X .

▲ D(X +C) = M[(X +C) −M(X +C)]2 = M(X −M X )2 = D X ■. D3). Константа из-под знака дисперсии выносится с квадратом:

D(CX ) =C2 D X .

▲ D(CX ) = M[CX −M(CX )]2 =C2 M(X −M X )2 = D X ■.

28

Дисперсия имеет размерность квадрата случайной величины. Характеристикой рассеивания, размерность которой совпадает с размерность случайной величины, является среднее квадратическое отклонение σX

(стандартное отклонение), определяемое как корень арифметический из дисперсии:

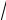σX = DX .

Поэтому часто пишут: DX =σX2 .

Другие используемые на практике числовые характеристики положения. Величина xp , определяемая равенством F (xp )= p , называется

p - квантилем распределения случайной величины X .

Квантиль x0,5 называется медианой распределения случайной величины X . Другими словами, медиана – это значение x0,5 на числовой прямой, для

которого

P(X ≤ x0,5 ) = P(X ≥ x0,5 ) = 0,5

Модой распределения непрерывной случайной величины X называется число xM , при котором плотность вероятностей f (x) достигает максимального

значения. Распределения с одной модой называются унимодальными, а распределения с несколькими модами – мультимодальными.

Для симметричных распределений медиана, мода и математическое ожидание совпадают.

2.7. Числовые характеристики дискретных и непрерывных случайных величин

1. Индикаторная случайная величина. Индикаторная случайная величина имеет вид:

29