48. Определение производной. Односторонние произ. Примеры без произв.

ОПР1: Производной ф-ии f(x) в точке называется предел отношения приращения значения ф-ии к приращению фргумента, когда последний стремится к 0, если этот предел существует и конечен.ОПР2: еслиf(x) определена в правой или левой окрестности (.)то можно определить правую и левую производную:(2)(3). Правая и левая производные также называются односторонними. Примеры функций не имеющих производной в точке:y=|x|в (.)0 но есть правая и левая, y=xsin(1/x) в 0 нет правой и левой.

49. Механический смысл: закон движения мат точки:S=S(t) t-время S-расстояние. За промежуток ∆t начиная от t0 пройдет путь ∆S=S(t0+∆t)-S(t0). Средняя скорость vср= (S(t0+∆t)-S(t0))/ ∆t. Если ∆t->0 то получим мгновенную скорость. Если существует то его обозначаютv(t0). Производная выражает скорость изменения некоторой величины в (.).Геометрический смысл: производная равна угловому коэф касательной к графику ф-и в (.) касания.ур-е касательной:Нормаль:

50. Определение ф-ии, дифф. В точке: ф-я y=f(x): IcR->R называется дифференцируемой в (.)если ее приращениеможно представить в видегдеA- конечное число. Теорема1: для того чтобы ф-я y=f(x) была дифференц в (.)необход и достат сущ конечной производнойв (.)причем значение. Докво: (=>)если ф-я дифф в (.)то выполнится соотношение (1) деля которое наи переходя к пределу приполучим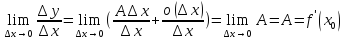(<=)пусть в (.)сущ конеч произтогда=>:=>. Теорема2: если ф-яf(x) диф в (.)то она напрерывна в этой точкеДокво:

51. Вывод формул производных суммы, произведения, частного функций. Сумма: (u(x)±v(x))’= u’(x)±v’(x): дадим приращениеПроиз:Частное:.

52. Теорема сложной функции. Если y=g(x) диффер в (.)а ф-яz=f(y) дифф в (.)(.)то сложная ф-яz=f(g(x)) будет дифф в (.)причем(1) Докво:где альф->0 при ∆y->0. Разделив (2) на ∆х и перейдя к пределу: +=

53. Теорема о производной обратной ф-и. если ф-я y=f(x) имеет в (.)произвтогда ф-яx=ϕ(y) также имеет в (.)прроизвод причем(4) Докво: дадим аргументуy обратной ф-и ϕ(y) приращение ∆y тода и х получит приращение ∆х≠0 и мы можем записать перейдя к пределу получим\

54.Диффер функ параметрич и неявно. Функция параметрически: задана f(x)= если ф-иидиффер приt=t0 причем то ф-ияy=f(x) также диффф в(.)х0=и произ находится по формуле. Неявно: пусть ф-яy=f(x) задано неявно соотношением F(x;y)=0 . Для нахождения производной y’=f’(x) нужно продиффер ф-ю F(x,f(x))=0 считая х независимой переменной а y-ее ф-ей.

55.Определение дифференциала. Величина f’(x0)∆x являющаяся главной при f’(x0)≠0 частью приращения линейной относит ∆х – дифференциал ф-ии y=f(x) в (.)x0 и обознач df(x0). Геометрически дифференциал есть приращение ординаты касательной проведенной к графуку f(x) в (.)x0 при переходе от (.)х0 к х0+∆х. Из геом смысла и формулы ∆y(x0)=f’(x0)∆x+o(∆x) получаем ∆y(x0)≈dy(x0) откуда f(x0+∆x)-f(x0)≈f’(x0)∆x => f(x0+∆x)≈ f(x0)+f’(x0)∆x. Найти значение

56.определение производных и дифференциалов высших порядков . ОПР1: пусть ф-я y=f(x) имеет в (.)х производную f’(x) которая в свою очередь явл дифф-мой в (.) х. Производная (y’(x))’=(f’(x))’ от произв первого порядка называется производ второго порядка и обознач f’’(x) . ОПР2: аналогично если сущ (n-1) производная и ф-я y=f(x) диф в (.)х то ()’ произn-ого порядка.также как и производные высшего порядка диф-ы ыс пор определяются индуктивноПример:. Для ф-й заданных параметрически: пустьx(t) y(t)- дважды диф по t, тогда 3-я и послед находятся аналогично. Для ф-й заданных неявно: нахождение первой производной явное выделение и послед диф-е.

57. диффе-л слож ф-ии первого и высших порядков. Инвариантность формы первого диф-ла. Свойством инвариантности обладают диф-лы 1 порядка, но диф-лы высших порядков этим свойством е обладают. Под свойством инвариантности понимают св-во ди-лов сохранять вид вне зависимости от тго является ф-я сложной или нет. Докажем это. Диф-л первого порядка сложной функции находится:y=f(x) dy=f’(x)dx. пусть x=ϕ(t) t-незав переменная однако для д-лов высших порядков св-во инвар нарушается:–св инвар нар.

58.Теорема Ферма о диф ф-и. Если ф-я f(x) диф в (.) х0 – точка экстремума, то f’(x0)=0 будем считать х0-т максимума тогда пусть- левой полуокр (.)х0.аналогично для правой полуокрестности<0 тк=>f’(x0)=0

59. Теорема Ролля и ее геометрич смысл. Пусть f(x) непрерывна на отрезке [a;b] диффрен на интервале (a;b) и на концах отрезка принимает одинаковые значения f(a)=f(b) тогда найдется хотя бы одна (.)такая чтоf’()=0. (fϵC[a;b]^fϵD(a;b)^f(a)=f(b))=>() Докво: ткfϵC[a;b] то найдутся точки отрезка[a;b] в которых f(x) достигает свое наименьшее m и наибольшее M значение. Если m=M то f(x) на отрезке[a;b] постоянна а значит f’(x)=0 и в качестве (.) можно выбирать любую точку. Предположимm≠M тогда имеет место один из вариантов: a) f(a)=f(b)>m b) (a)=f(b)<M но тогда это означает что точки х* и х** - экстремальные и по теореме Ферма произ=0 и в качестве пси можно взять эти точки. Геометрич смысл:

60. Теорема Лагранжа. Если f(x) непрерывна на отрезке [a;b] и диф в интервале(a;b) то найдутся (.)ξ из интервала C такая что f(b)-f(a)=f’(ξ)(b-a) Докво: рассмотрим вспомогат ф-ю F(x)=f(x)-λx значение λ выберем из условия F(a)=F(b) тогда:ф-яF(x) удовлет всем условиям теоремы Ролля при выбранной λ F(a)=F(b)=>Геометрически: найдется (.)ξ в которой касательная к графику будет паралельна хорде соед точкиA(a,f(a)) B(b,f(b))