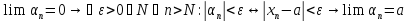- •7.Дать определения а)числовой последовательности,б)ограниченной числовой послед в)предела числовой последовательности
- •9. Сформ-ь и док-ть св-ва последоват всязанные с неравенст
- •10. Сформулировать и док-ть теорему о пределе «зажатой» послед.
- •13.Теорема о связи членов сходящ последоват со своим пределом и беск малой
- •14. Теорема об арифмет операциях со сходящ послед
- •15. Определение точных верх и ниж граней числовых сножеств. Теорема о существовании точных граней огранич числ множ.
- •16.Признак сходимости монотонной последовательности.
- •17. Число e. Второй замечательный предел.
- •18.Подпоследовательности. Теорема Больцано-Вейерштрасса.
- •19. Предельные точки. Фундаментальные последовате. Критерий коши.
- •20.Конечный предел функции в точке при . Определение по Коши и п Гейне. Геометр интерпретация. Эквивалентность опр предела.
- •21.Одностороние пределы. Теорема о существовании предела в точке.
- •48. Определение производной. Односторонние произ. Примеры без произв.
- •61.Теорема Коши о конечных приращ
- •63.Формула Тейлора с остаточным членом в форме Пеано.
- •65. Формула Тейлора с остаточным членом в форме Лагранжа.
- •66.Теорема о необходимых и достаточных условиях возраст и убывания дифф функции.
- •67.Необходимое условие существования экстремума
- •69.Второй достаточный признак существования экстремума.
7.Дать определения а)числовой последовательности,б)ограниченной числовой послед в)предела числовой последовательности
Опр1:
Пусть каждому натуральному числу
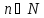 поставлено в соответствие по определенному
закону единственное число
поставлено в соответствие по определенному
закону единственное число
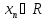 .
Тогда множество пронумерованных чисел
х1,х2,х3 и т.д называется числовой
последовательностью. Обычно обозначают
так
.
Тогда множество пронумерованных чисел
х1,х2,х3 и т.д называется числовой
последовательностью. Обычно обозначают
так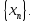
Опр1:
Числовой последовательностью называется
отображение
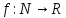 . Обычно последовательность задают с
помощью формулы, позволяющей вычислить
ее элемент по номеруn.
. Обычно последовательность задают с
помощью формулы, позволяющей вычислить
ее элемент по номеруn.
Опр3:
Последовательность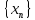 называется:
называется:
Ограниченной
сверху, если
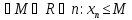 ;
;
Ограниченной
снизу, если
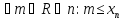 ;
;
Ограниченной,
если
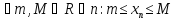 .
.
Легко
видно, что свойства последовательности
быть ограниченной означает, что

Опр4:
Число а называется пределом
последовательности
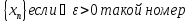 n,
что все члены последовательности с
номером >n
будут удовлетворять неравенству
n,
что все члены последовательности с
номером >n
будут удовлетворять неравенству
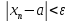 (1). При этом принято писать
(1). При этом принято писать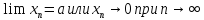 .
Опр4 можно записать с помощью символов
мат логики. В результатах получим
.
Опр4 можно записать с помощью символов
мат логики. В результатах получим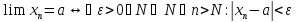 (2)
(2)
8.Сформулировать и доказать сво-ва сходящейся последоват.
Т1:
Любая окрестность предела сходящ
последоват содержит все члены
последовательности, за исключением их
конечного числа.![]()
Док-во:
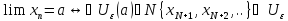 т.е
т.е
Т2:Сходящаяся последовательность имеет единственный предел.
Док-во:
Предположим противное. Пусть
последовательность xn
имеет 2 предела а1 и а2, причем a1<a2.
Т.к. а1≠а2 то согласно принципу отдельности
Хаусдорфа,
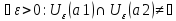
![]()
Возьмем
данное
 и зафиксируем его т.к
и зафиксируем его т.к
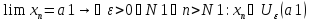

Если
взять N=max{N1,N2},
то мы получим, что
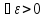 такое, чтоN>N
такое, чтоN>N
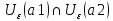 ,
что противоречит свойству Хаусдорфа.
,
что противоречит свойству Хаусдорфа.
Т3: Если последовательность сходится, то она ограничена.
Нам
нужно доказать, что если
 ,
то
,
то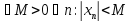 ,
т.к
,
т.к а
значит и для
а
значит и для найдется такой номерN,
что
найдется такой номерN,
что
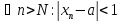 ,
дляn>N:|
,
дляn>N:|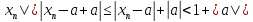 .
Выберем в качестве числаM=max{|
.
Выберем в качестве числаM=max{|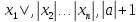 }
Тогда #.
}
Тогда #.
9. Сформ-ь и док-ть св-ва последоват всязанные с неравенст
Т1:
пусть
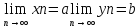 a<b
тогда сущ NϵN
для любого n>N:
xn<yn.
Док-во: тк a≠b
то по св-ву отделимости Хаусдорфа
a<b
тогда сущ NϵN
для любого n>N:
xn<yn.
Док-во: тк a≠b
то по св-ву отделимости Хаусдорфа

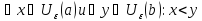 зафиксир
зафиксир
 аналогич
аналогич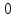
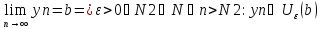 возьмемN=max{N1,N2}
и получим что одновременно все
возьмемN=max{N1,N2}
и получим что одновременно все
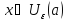 и все
и все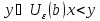 .
Т2: если
.
Т2: если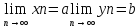
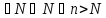 xn≤yn
то a≤b
Докво: предположим противное, тогда
согласно Т1 все члеы послед xn
yn
с некотрого номера начнут удовл
неравенству xn
>yn
что противоречит условию теоремы.
xn≤yn
то a≤b
Докво: предположим противное, тогда
согласно Т1 все члеы послед xn
yn
с некотрого номера начнут удовл
неравенству xn
>yn
что противоречит условию теоремы.
10. Сформулировать и док-ть теорему о пределе «зажатой» послед.
Пусть
числовые послед {xn}
{yn}
{zn}
удовлет условию сущ N0ϵN
для любого n>N0
xn≤yn≤zn
(*) если {xn}
и{zn}
сход к одному и тому же пределу то и
{yn}
сходится к этому пределу.
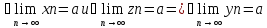 Док-во:
Док-во:
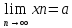 =>
=>
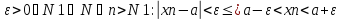 (**) аналогично
(**) аналогично (***) возьмемN=max{N0,N1,N2}
и получим
(***) возьмемN=max{N0,N1,N2}
и получим
 =>
=>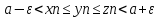 <=>
<=>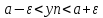 |yn-a|<
|yn-a|<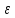 =>
=>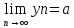
11.Бесконечно большие и малые последовательности.
Опр: Последовательность {Xn} называется бесконечно большой если ее предел равен бесконечности(-+).
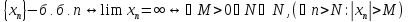
Опр:
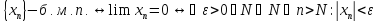
T8:
Пусть
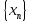 и
и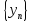 являются б.м.н. Тогда последоват
являются б.м.н. Тогда последоват так же являются б.м.п
так же являются б.м.п
Док-во:
Докажем что
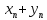 -
б.м.п. Возьмем
-
б.м.п. Возьмем и зафиксируем его. Т.к
и зафиксируем его. Т.к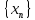 – б.м.п
– б.м.п
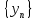 –б.м.п
–б.м.п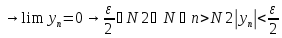 .
В результате мы получили, что
.
В результате мы получили, что
T10:
Если

12.Теорема о произведении ограниченной послед на бесконечно малую.
Т9:
Произведение
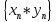 ограниченной
последовательности
ограниченной
последовательности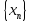 на б.м.п
на б.м.п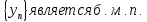
Док-во:
Т.к
 то
то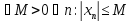 .
Т.к.
.
Т.к.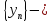 б.м.п,
то
б.м.п,
то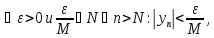 в
результате получаем что
в
результате получаем что .
.
13.Теорема о связи членов сходящ последоват со своим пределом и беск малой
T11:
Послед {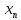 }
сходится к пределуa
}
сходится к пределуa
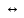 существует бесконечно малая
существует бесконечно малая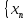 }:
}: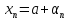
Док-во:
( )
Пусть
)
Пусть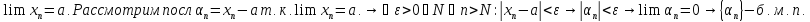
( )
)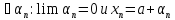
Докажем,
что
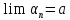 .
.
Т.к.