
- •7.Дать определения а)числовой последовательности,б)ограниченной числовой послед в)предела числовой последовательности
- •9. Сформ-ь и док-ть св-ва последоват всязанные с неравенст
- •10. Сформулировать и док-ть теорему о пределе «зажатой» послед.
- •13.Теорема о связи членов сходящ последоват со своим пределом и беск малой
- •14. Теорема об арифмет операциях со сходящ послед
- •15. Определение точных верх и ниж граней числовых сножеств. Теорема о существовании точных граней огранич числ множ.
- •16.Признак сходимости монотонной последовательности.
- •17. Число e. Второй замечательный предел.
- •18.Подпоследовательности. Теорема Больцано-Вейерштрасса.
- •19. Предельные точки. Фундаментальные последовате. Критерий коши.
- •20.Конечный предел функции в точке при . Определение по Коши и п Гейне. Геометр интерпретация. Эквивалентность опр предела.
- •21.Одностороние пределы. Теорема о существовании предела в точке.
- •48. Определение производной. Односторонние произ. Примеры без произв.
- •61.Теорема Коши о конечных приращ
- •63.Формула Тейлора с остаточным членом в форме Пеано.
- •65. Формула Тейлора с остаточным членом в форме Лагранжа.
- •66.Теорема о необходимых и достаточных условиях возраст и убывания дифф функции.
- •67.Необходимое условие существования экстремума
- •69.Второй достаточный признак существования экстремума.
19. Предельные точки. Фундаментальные последовате. Критерий коши.
Т19(Критерий предельной точки).
Пусть
мн-во
 является
бесконечным множеством, тогда точка х0
является предельной точкой, если найдется
такая последовательность точек
является
бесконечным множеством, тогда точка х0
является предельной точкой, если найдется
такая последовательность точек ,
предел которой равен этой точке.
,
предел которой равен этой точке.
Т20(критерий Коши).
Последовательность сходится т.т.т.к. она является фундаментальной.
20.Конечный предел функции в точке при . Определение по Коши и п Гейне. Геометр интерпретация. Эквивалентность опр предела.
1)(→)
Пусть выполняется определение по Коши, т.е.

Поскольку
 ,
фигурирующее в данном определении,
сущест то зафиксируем его. Рассмотрим
последовательность {
,
фигурирующее в данном определении,
сущест то зафиксируем его. Рассмотрим
последовательность {
В
итоге мы получили что

2)(←)
Пусть выполняется определение по Гейне, т.е.:

Предположим
противное

Согласно построенному выше отрицанию это означает, что:

Поскольку
у нас фигурирует произвольное значение
 ,
так выберем целую последовательность
, что
,
так выберем целую последовательность
, что
Мы
получаем:

Что противоречит условию определения предела по Гейне.
21.Одностороние пределы. Теорема о существовании предела в точке.
Т2. Функция f(x) имеет в точке а предел А т.т.т.к. в этой точке она имеет односторонние пределы и они равны А.
Док-во: 1)(→)
Пусть существует предел функции f(x)

Отсюда
следует определение односторонних
преелов
 и
и

2)(←)

Возьмем
произвольное
 и
зафиксируем его. Тогда:
и
зафиксируем его. Тогда:
Если
взять в качестве


22.Конечный
предел функции при при
 .
Геометр иллюстрация. Горизонт асимптоты.
.
Геометр иллюстрация. Горизонт асимптоты.
Понятие
предела функции при
 очень похоже на понятие предела
последовательности и имеет с ним много
общих черт. Запишем эти определения в
символической форме и дадим им геометрич
интерпретацию.
очень похоже на понятие предела
последовательности и имеет с ним много
общих черт. Запишем эти определения в
символической форме и дадим им геометрич
интерпретацию.



Поскольку
условие
 ,
что означает, что значения функции лежат
в 1-ой полосе (.)А, то с геометрической
точки зрения это означает, что, начиная
с некоторого числа Н(по смыслу достаточно
большого) значения функции отличаются
от А меньше, чем на
,
что означает, что значения функции лежат
в 1-ой полосе (.)А, то с геометрической
точки зрения это означает, что, начиная
с некоторого числа Н(по смыслу достаточно
большого) значения функции отличаются
от А меньше, чем на .
.
Мы видим, что при больших значениях Х, график функции f(x) неограниченно приближается к прямой у=А. Такую прямую принято называть горизонтальной асимптотой.
Замечание:
Вообще говоря, на - и +
и + функцияf(x)
может иметь разные горизонтальные
асимптоты.
функцияf(x)
может иметь разные горизонтальные
асимптоты.
23. Бесконечный предел функции в конеч точке. Геометр иллюстр. Вертикальные асимптоты.
Путь
функция f(x)
определена в некоторой последовательность
(.)а, кроме может быть, самой (.)а.
Опр:
Говорят, что функция f(x)
имеет в (.) бесконечный предел, и пишут
бесконечный предел, и пишут
Такие функции называются бесконечно большими.
Если для достаточно больших некоторых значений аргументы приближенные к (.)а функция f(x) принимает только отрицательные или только положительные значения, то пишут


Геометрически определение б.б.ф. означает, что для любого М>0 мы можем подойти к предельной точке а на столько близко, что значения функции в этих точках превзойдет выбранное М.
Существование у функции f(x) бесконечного предела в конечной (.)а означает, что график функции f(x) неограниченно приближается к прямой x=a, а значит, эта прямая является вертикальной асимптотой данной функции.
24.Св-ва
ф-и имеющих конечный предел.
св-во 1(единственность предела) Если
фушкция f(x)
в (.) а имеет предел то он единственен.
Докво: Предположим противоположное,
что функция f(x)
при х->a
имеет 2 предела А1 и А2. Но тогда для
 .
Согласно опр предела по Гейне (опр 2)
послед значений функции f(x)
{f(x)}
должна стремиться и к А1 и к А2, которые
не равны м\у собой, что противоречит
единственности предела сходящ
последовательностей.
.
Согласно опр предела по Гейне (опр 2)
послед значений функции f(x)
{f(x)}
должна стремиться и к А1 и к А2, которые
не равны м\у собой, что противоречит
единственности предела сходящ
последовательностей.
Св-во
2(ограниченность) Если ф-ия f(x)
имеет предел в(.)а то найдется такая
окрестность точки а в которой ф-ия
ограничена. Докво: пусть
 ,
а АϵR,
тогда
,
а АϵR,
тогда

Св-во
3(сохранение знака) Если ф-ия f(x)
имеет конечный предел в (.) а отличный
от 0 то найдется такая окрестность точки
а в которой ф-ия f(x)
имеет знак своего предела. Докво:
 .
.
25.
теорема о пределе зажатой ф-ии.
св-во 4 Если
 и
существует такая окрестность точки
а(возможно проколотая), чтоf(x)≤h(x)≤g(x)
nj
и
существует такая окрестность точки
а(возможно проколотая), чтоf(x)≤h(x)≤g(x)
nj
 .
Док-во: Пусть
.
Док-во: Пусть Тк
Тк ,
Аналогично
,
Аналогично ,
Врезультате получаем что
,
Врезультате получаем что
26.
Предел суммы.
Если ф-ии f(x)
и g(x)
имеют в (.) а конечные пределы А и В
соответсвенно то: 1)
 Докво: тк
Докво: тк Выбирая
Выбирая получаем:
получаем:
27.
Предел произведения
Если ф-ии f(x)
и g(x)
имеют в (.) а конечные пределы А и В
соответсвенно то: 2)
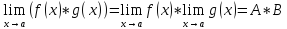 Докво: Возьмем некоторую последовательность
Докво: Возьмем некоторую последовательность имеющую
своим пределомa.
Тогда согласно определению предела
имеющую
своим пределомa.
Тогда согласно определению предела

 и из свойств сходящихся
последовательностей(предел произведения
последовательностей= произведению
пределов ) следует предела
и из свойств сходящихся
последовательностей(предел произведения
последовательностей= произведению
пределов ) следует предела
 а тк Хн – произвольная последовательнсть
то справедливо
а тк Хн – произвольная последовательнсть
то справедливо
28.
Предел частного
Если ф-ии f(x)
и g(x)≠0
имеют в (.) а конечные пределы А и В
соответсвенно то: 2)
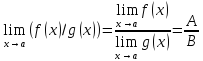 Докво: Возьмем некоторую последовательность
Докво: Возьмем некоторую последовательность имеющую
своим пределомa.
Тогда согласно определению предела
имеющую
своим пределомa.
Тогда согласно определению предела

 и из свойств сходящихся
последовательностей(предел частного
последовательностей= частному пределов
) следует предела
и из свойств сходящихся
последовательностей(предел частного
последовательностей= частному пределов
) следует предела
 а тк Хн – произвольная последовательность
то справедливо
а тк Хн – произвольная последовательность
то справедливо .
.
29.
Теорема о пределе сложной функции.
Если ф-ия y=f(x)
имеет в (.) а конечный предел b
в некоторой проколотой окрестности
(.)а
 ,
а ф-ияg(y)
имеет в точке b
конечный предел c
, то сложная ф-ия g(f(x))
имеет в точке а предел c
,
а ф-ияg(y)
имеет в точке b
конечный предел c
, то сложная ф-ия g(f(x))
имеет в точке а предел c
 Докво: тк
Докво: тк Возьмем
любую последовательность {Xn}
Xn≠a
сходящуюся
Возьмем
любую последовательность {Xn}
Xn≠a
сходящуюся
 все члены которой начиная с некоторого
номера попадут в
все члены которой начиная с некоторого
номера попадут в где
значения
где
значения фигурирует в условии теоремы. Тогда для
данной последовательности
фигурирует в условии теоремы. Тогда для
данной последовательности все члены последов
все члены последов будут отличны отb
В результате мы получаем что:
будут отличны отb
В результате мы получаем что:

30.бб
и бм ф-ии и их пределы.ОПР.Если
при x->
a
предел функции f(x)
равен ∞(-∞,+∞), то она называется
бесконечно большой функцией при x->a.
То
 ОПР. Если приx->
a
предел функции f(x)
равен 0, то она называется бесконечно
малой функцией при x->a.
То
ОПР. Если приx->
a
предел функции f(x)
равен 0, то она называется бесконечно
малой функцией при x->a.
То
 Теорема о связи бб и бм ф-й: Если функция
α(x)-бмф
при x->a
и α(x)≠0,
то функция 1/( α(x))-ббф
при x->a.
Верно и обратное. Теорема о связи функции
ее предела и бм:
Теорема о связи бб и бм ф-й: Если функция
α(x)-бмф
при x->a
и α(x)≠0,
то функция 1/( α(x))-ббф
при x->a.
Верно и обратное. Теорема о связи функции
ее предела и бм:
 f(x)=A+
α(x)
Докво: Необходимо
показать, что
f(x)=A+
α(x)
Докво: Необходимо
показать, что
 <=> f(x)-A б.м.
функция при x->a.
Так как
<=> f(x)-A б.м.
функция при x->a.
Так как  ,
то
,
то для
для будет
выполняться неравенство
будет
выполняться неравенство .
Сравним это с определением б. м. функции:
.
Сравним это с определением б. м. функции: для
для будет
выполняться неравенство
будет
выполняться неравенство .Сравнивая
определения предела функции и б. м.
функции, видим, чтоf(x)-A - б.м.
при x->a.
Некоторые свойства: 1)Сумма
конечного числа БМ при x->a функций есть
БМ функция 2) Произведение конечного
числа БМ на при x->a есть БМ при x->a
функция 3) Произведение оганиченной
величины на беск малую при x->a есть БМ
при ->a функция
.Сравнивая
определения предела функции и б. м.
функции, видим, чтоf(x)-A - б.м.
при x->a.
Некоторые свойства: 1)Сумма
конечного числа БМ при x->a функций есть
БМ функция 2) Произведение конечного
числа БМ на при x->a есть БМ при x->a
функция 3) Произведение оганиченной
величины на беск малую при x->a есть БМ
при ->a функция
31.
первый замечательный предел
 Док-во угол AOB=x
пусть хϵ (0;pi/2)
тогда длина дуги BA=x
пусть S1,
S2,
S3
–площади треуг AOB,
сектора AOB
и треуг COB.
S1=1/2*OB*AD=1/2*sinx;
S2=1/2 OB^2*x; S3=1/2*OB*CB=1/2tgx. Поскольку
фигура AOB
лежит в секторе AOB
а сектор в фигуре COB
то S1<S2<S3
или sinx<x<tgx.
Поскольку в 1-ой четверти sinx>0
то
Док-во угол AOB=x
пусть хϵ (0;pi/2)
тогда длина дуги BA=x
пусть S1,
S2,
S3
–площади треуг AOB,
сектора AOB
и треуг COB.
S1=1/2*OB*AD=1/2*sinx;
S2=1/2 OB^2*x; S3=1/2*OB*CB=1/2tgx. Поскольку
фигура AOB
лежит в секторе AOB
а сектор в фигуре COB
то S1<S2<S3
или sinx<x<tgx.
Поскольку в 1-ой четверти sinx>0
то
 по теореме о зажатой ф-ии тк
по теореме о зажатой ф-ии тк поскольку
функция
поскольку
функция нечетная
то все послед. Выкладки будут истинны.
нечетная
то все послед. Выкладки будут истинны.
32.
Сравнение бм функций
Пусть α(x)
и β(x)
–бмф при x->a
. β(x)≠0
при
 .
ОПР1 бмф α(x)
и β(x)
– ф-ии одного порядка малости при x->a
если
.
ОПР1 бмф α(x)
и β(x)
– ф-ии одного порядка малости при x->a
если
 .В этом случае пишут α(x)
=О(β(x))
при x->a.
ОПР2 бмф α(x)
называют бесконечно малой более высокого
порядка малости при x->a
чем β(x),
если
.В этом случае пишут α(x)
=О(β(x))
при x->a.
ОПР2 бмф α(x)
называют бесконечно малой более высокого
порядка малости при x->a
чем β(x),
если
 Пишут α(x)
=о(β(x))
при x->a.
Теорема 1: следующие условия эквивалентны:
1) f(x)=O(g(x))при
x->a
2)
Пишут α(x)
=о(β(x))
при x->a.
Теорема 1: следующие условия эквивалентны:
1) f(x)=O(g(x))при
x->a
2) 3)f(x)=α(x)g(x)
где α(x)-бмф
при x->a.
Докво: то что 12
следует из ОПР2. Докажем что 23
(=>)23
тк
3)f(x)=α(x)g(x)
где α(x)-бмф
при x->a.
Докво: то что 12
следует из ОПР2. Докажем что 23
(=>)23
тк
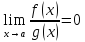 =>[по теореме связи функции, предела и
бмф]=>
=>[по теореме связи функции, предела и
бмф]=> .
(<=)Докажем что 3=>2: )f(x)=α(x)g(x)=>
.
(<=)Докажем что 3=>2: )f(x)=α(x)g(x)=>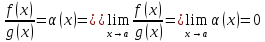 .
ОПР3 бмф
.
ОПР3 бмф называет бесконечно малой к-того порядка
малости по сравнению с бмф
называет бесконечно малой к-того порядка
малости по сравнению с бмф если
если
33.
Эквивалентные функции.
Пусть f(x)и
g(x)
определены в некоторой окрестности
(возможно проколотой) (.) а и g(x)≠0
в этой окрестности. ОПР4 функции f(x)и
g(x)
называются эквивалентными или
асимптотически равными при x->a
если
 пишутf(x)
пишутf(x) g(x)
при x->a
. Теорема 2. Для того чтобы ф-ии f(x)и
g(x)
были эквивалентными при x->a
(=>)и(<=) чтобы f(x)=g(x)+о(g(x))
при x->a
(4). Докво: (=>) пусть f(x)и
g(x)
– эквивалетны тогда выполняется формула
(3)
g(x)
при x->a
. Теорема 2. Для того чтобы ф-ии f(x)и
g(x)
были эквивалентными при x->a
(=>)и(<=) чтобы f(x)=g(x)+о(g(x))
при x->a
(4). Докво: (=>) пусть f(x)и
g(x)
– эквивалетны тогда выполняется формула
(3) (по теореме освязи функции предела и
бм), где
(по теореме освязи функции предела и
бм), где
 g(x)+о(g(x)).
(<=) пусть выполняется (4), тогда
g(x)+о(g(x)).
(<=) пусть выполняется (4), тогда перейдя к пределу приx->a
получим в силу теорм1(п3) формулу(3). След1
Если
перейдя к пределу приx->a
получим в силу теорм1(п3) формулу(3). След1
Если
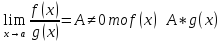 Док-во:
Док-во: .
След2: разность эквивалетных бм есть бм
более высокого порядка малости чем
каждая из них. Докво: пусть
.
След2: разность эквивалетных бм есть бм
более высокого порядка малости чем
каждая из них. Докво: пусть .
ОПР5 Еслиf(x)=g(x)+о(g(x))
.
ОПР5 Еслиf(x)=g(x)+о(g(x)) тоg(x)
называют главной частью ф-ии f(x)
тоg(x)
называют главной частью ф-ии f(x)

34.
Вычисление пределов с помощью эквивалетных
Теорема 3. f(x) g(x)
при x->a
то 1)
g(x)
при x->a
то 1) ;
2)
;
2) Докво: 1)
Докво: 1) ;
2)
;
2) (предел частного эквивалетных равен
1). Теорема 4 Сумма бм разного порядка
эквивалентна бм наинизшего порядка
малости. Докво: пусть
(предел частного эквивалетных равен
1). Теорема 4 Сумма бм разного порядка
эквивалентна бм наинизшего порядка
малости. Докво: пусть будем считать что бм
будем считать что бм -
бм наинизшего порядка по сравнению с
другими те
-
бм наинизшего порядка по сравнению с
другими те тогда
тогда
35.
Асимптоты графика функций.
ОПР:прямая y=kx+b
явл асимптотой бесконеч веттви y=f(x)при
x->+-∞
если расстояние между точкой принадлежащей
прямой и y=kx+b
стремится к 0 при x->+-∞
Теорема: прямая y=kx+b
явл асимптотой графика в-ии y=f(x)при
x->+-∞
тттк
 Докво:
(=>) Пусть выполняется условия (*)(**)
тогда нужно доктьf(x)=kx+b+o(x),
x->+∞(-∞).
Из условия (**)=> по теореме о связи ф-ии
предела и бм что
Докво:
(=>) Пусть выполняется условия (*)(**)
тогда нужно доктьf(x)=kx+b+o(x),
x->+∞(-∞).
Из условия (**)=> по теореме о связи ф-ии
предела и бм что (<=) пусть выполняетсяf(x)=kx+b+o(x)
x->+∞(-∞).
Деля на х и перейдя к пределу получаем
усл (*). Усл (**) будет выполняться из того
же соотношения.
(<=) пусть выполняетсяf(x)=kx+b+o(x)
x->+∞(-∞).
Деля на х и перейдя к пределу получаем
усл (*). Усл (**) будет выполняться из того
же соотношения.
36.
Критерий Коши.
Теорема: предел ф-ии f(x)при
x->a
существует тттк для
 Докво: (=>) пусть
Докво: (=>) пусть тогда
тогда справедливо |f(x)-a|<
справедливо |f(x)-a|< /2
поэтому если
/2
поэтому если и
и |f(x’’)-f(x’)|=|[f(x’’)-a]+[a-f(x’)]|≤
|f(x’’)-a]+[a-f(x’)|≤
|f(x’’)-f(x’)|=|[f(x’’)-a]+[a-f(x’)]|≤
|f(x’’)-a]+[a-f(x’)|≤ /2+
/2+ /2=
/2= .
(<=) пусть произвольно фиксировано
.
(<=) пусть произвольно фиксировано >0
тогда сущ-ет окрест
>0
тогда сущ-ет окрест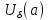 что для всехx’
что для всехx’ x’’
x’’ выполнится неравентсво |[f(x’)-
f(x’’)]<
выполнится неравентсво |[f(x’)-
f(x’’)]< докажем что в (.) а ф-я имеет предел. По
опр предела Гейне пусть {xn}-произв
послед xn->a
n->inf.
Фиксируем
докажем что в (.) а ф-я имеет предел. По
опр предела Гейне пусть {xn}-произв
послед xn->a
n->inf.
Фиксируем
 в силу определ найдется такой номер что
в силу определ найдется такой номер что выполнится
условие
выполнится
условие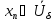 ,
, тогда по условию Коши
тогда по условию Коши что означает что
что означает что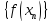 - фундаментальна
- фундаментальна сходщ к некотор числу А.
сходщ к некотор числу А.
38.
два определения функции непрерывной в
точке. ОПР1
функция непрерывна, когда она определена
в окрестности (.)х, в (.)х и
 :fϵC(
:fϵC( )
ОПР2 функция непрерывна если определена
в (.)х и бесконечно малому приращению
аргумента соответствует бм приращение
функции:
)
ОПР2 функция непрерывна если определена
в (.)х и бесконечно малому приращению
аргумента соответствует бм приращение
функции: .
Докажем эквивалентность: из условий
Опр1
.
Докажем эквивалентность: из условий
Опр1 .
.
39.
Точки разрыва и их классификация.
Ф-ия f(x)
называется разрывной в(.) ,
а
,
а называется точкой разрыва если она не
явл в этой точке непрерывной.
называется точкой разрыва если она не
явл в этой точке непрерывной.
Классификация:
Если
предел
 существует, но не равен
существует, но не равен или это значение не существует то точка
или это значение не существует то точка - устранимая.
- устранимая.
Если
существуют односторонние пределы
 – точка разрыва типа скачка причем
– точка разрыва типа скачка причем -величина
скачка. 1 и 2 – тр первого рода.
-величина
скачка. 1 и 2 – тр первого рода.
Если
е сущ хотябы один одностор предел в(.) или он равен
или он равен
 -точка
разрыва второго рода.
-точка
разрыва второго рода.
40.
Свойства функций непрерывных в точке.
СВ1 если fϵC( )
то найдется такая окрест (.)
)
то найдется такая окрест (.) в которой функцияf(x)
ограничена. СВ2 если функция f(x)
непрерывна в (.)
в которой функцияf(x)
ограничена. СВ2 если функция f(x)
непрерывна в (.) и
и то найдется такая окрестность (.)
то найдется такая окрестность (.) в которой знак ф-ии совпадает со знаком
в которой знак ф-ии совпадает со знаком .
СВ3 Еслиf,gϵC(
.
СВ3 Еслиf,gϵC(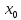 )
и
)
и то найдется такая окрестность (.)
то найдется такая окрестность (.) =>
=> СВ4 Еслиf(x),g(x)ϵC(
СВ4 Еслиf(x),g(x)ϵC( )
то в той же точке будет непрерывны ф-ии
)
то в той же точке будет непрерывны ф-ии
41.
Непрерывность сложной ф-ии.
Если функция g(x):
X->Y
непрерывна в (.)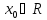 а функцияf(x):
Y->X
непрерывна в (.)
а функцияf(x):
Y->X
непрерывна в (.) то сложная функцияf(g(x)):X->Z
будет непреывна в (.)
то сложная функцияf(g(x)):X->Z
будет непреывна в (.) .
Докво: ЕслиfϵC(
.
Докво: ЕслиfϵC( gϵC(
gϵC( =>
для любого положит числа и для
=>
для любого положит числа и для (**)
Врезультате из условий (*)(**):
(**)
Врезультате из условий (*)(**): C(
C( ).
).
42.
теорема о нуле непрерывной на отрезке
функции.
Пусть ф-ия f(x)
непрерывна на отрезке [a;b]
и на концах этого отрезка имеет значения
разных знаков =>
 разделим отрезок [a;b]
пополам если значение ф-ии в середине
отрезка = 0 то мы нашли c=(a+b)/2.
Если это не так, выбираем тот из 2х
отрезков на концах которого f(x)
имеет разные знаки и опять делим,
продолжая мы либо найдем с, либо получим
систему отрезков
разделим отрезок [a;b]
пополам если значение ф-ии в середине
отрезка = 0 то мы нашли c=(a+b)/2.
Если это не так, выбираем тот из 2х
отрезков на концах которого f(x)
имеет разные знаки и опять делим,
продолжая мы либо найдем с, либо получим
систему отрезков которая
в силу построения является стягивабщйся
тк
которая
в силу построения является стягивабщйся
тк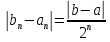 .
Мы получили возраст {
.
Мы получили возраст { }
и убыв{
}
и убыв{ }
пределом которых является с. В силу
непрерывности ф-ииf(x)
}
пределом которых является с. В силу
непрерывности ф-ииf(x) аналогично
аналогично =>f(c)=0
=>f(c)=0
43.
Теорема о промежуточных зачениях:
пусть ф-ия f(x)
непрерывна на [a;b]
и f(a)=A
и f(b)=B
тогда для любого значения С, A<C<B
 (fϵC[a;b]
и f(a)=A
и f(b)=b)=>(
(fϵC[a;b]
и f(a)=A
и f(b)=b)=>( )
Докво: расмотрим вспомаг функциюF(x)=f(x)-C
очевидно
FϵC[a;b], F(a)=A-C<0, F(b)=B-C>0=> по
теор1
)
Докво: расмотрим вспомаг функциюF(x)=f(x)-C
очевидно
FϵC[a;b], F(a)=A-C<0, F(b)=B-C>0=> по
теор1
 ;
F(c)=0 => f(c)-C=0 => f(c)=C
;
F(c)=0 => f(c)-C=0 => f(c)=C
44.
теорема об ограниченности непрерывной
функции.
Непрерывная на отрезке ф-ия ограничена
на этом отрезке
 )
док-во:
Докажем, что достигается sup (inf - аналогично).
Предположим,M-верхняя
грань что
)
док-во:
Докажем, что достигается sup (inf - аналогично).
Предположим,M-верхняя
грань что
 .
Рассмотрим вспомогательную функцию
.
Рассмотрим вспомогательную функцию
 ,
которая непрерывна и ограничена
на [a;b]:
,
которая непрерывна и ограничена
на [a;b]: .
.  , .
Таким образом
, .
Таким образом .
Но M - наименьшая из
верхних граней, а мы пришли к противоречию,
т. к.
.
Но M - наименьшая из
верхних граней, а мы пришли к противоречию,
т. к.  -
тоже верхняя грань. Теорема доказана.
-
тоже верхняя грань. Теорема доказана.
45.
Теорема о достижении непрерыв ф-ии своих
точных граней.
Если ф-ия f(x)
непрерывна на отрезке [a;b]
то найдутся (.)
 в которых ф-я f(x)
достигает своих точных нижней и верхней
грани. fϵC[a;b]=>(
в которых ф-я f(x)
достигает своих точных нижней и верхней
грани. fϵC[a;b]=>( ,
, :f(
:f( ,f(
,f( )=sup
f(x))как
мы щнаем если точка sup(inf)
принадлежит множеству то она называется
максимальным(минимальным) элементом.
m=min
f(x)
и M=max
f(x)
=> . fϵC[a;b]=>(
)=sup
f(x))как
мы щнаем если точка sup(inf)
принадлежит множеству то она называется
максимальным(минимальным) элементом.
m=min
f(x)
и M=max
f(x)
=> . fϵC[a;b]=>( ,
, :f(
:f( =m
,f(
=m
,f( )=M
– означает что ф-я в некоторых точках
достигает свое max
и min
знач.
)=M
– означает что ф-я в некоторых точках
достигает свое max
и min
знач.
46.теорема о непрерывности обратной функции. Теорема: строго монотонная и непрерывная на отрезке [a;b] ф-я f(x) имеет на отрезке с концами f(a) и f(b) обратную ф-ию, которая также явл строго монотонной с сохранением характера монотонности и непрерывности.
47.
определение и геометрическая интерпретация
равномерной непрерывности функции.
ОПР: ф-я f:
X->R,X
c
R
называется непрерывной на промежутке
Х если
 .
Геометрически: график функции не имеет
неограниченно крутых участков на Х.
Теорема Кантора о равномерности непрерыв:
Если ф-я f(x)
непрерывна на отрезке [a;b]
то она равномерно непрерывна на нем.
Докво: предположим противное
.
Геометрически: график функции не имеет
неограниченно крутых участков на Х.
Теорема Кантора о равномерности непрерыв:
Если ф-я f(x)
непрерывна на отрезке [a;b]
то она равномерно непрерывна на нем.
Докво: предположим противное возьмем значение
возьмем значение тогда
каждомуn
мы поставим в соответств
тогда
каждомуn
мы поставим в соответств
 те получить
те получить В силу условия
В силу условия также поскольку
также поскольку то
данные послед ограничены, а значит из
них можно извлечь сходящиеся причем к
одному знач,C
подпослед
то
данные послед ограничены, а значит из
них можно извлечь сходящиеся причем к
одному знач,C
подпослед
 ,
пользуясь непрерывностьюf
на [a;b]
получаем:
,
пользуясь непрерывностьюf
на [a;b]
получаем:
 -
- =
= - противоречие к
- противоречие к .
Следствие: если ф-яf(x)
непрерывна на отрезке [a;b]
то
.
Следствие: если ф-яf(x)
непрерывна на отрезке [a;b]
то
 если разбить [a;b]
на части отрезки с длинами меньшими
если разбить [a;b]
на части отрезки с длинами меньшими
 то разность значения функций предела
каждого частного отрезка будет меньшим
чем
то разность значения функций предела
каждого частного отрезка будет меньшим
чем
