
- •Формализм принципа максимума Понтрягина (вывод необходимых условий оптимальности)
- •Свойства функции Гамильтона и поиск ее экстремума
- •Типы граничных условий и виды краевых задач
- •Алгоритм применения принципа максимума Понтрягина
- •Оптимальное управление односекторной экономикой по критерию максимальной полезности
- •Оптимальное управление линейными системами
- •Решение линейных задач оптимального управления для экономических систем.
Оптимальное управление линейными системами
Постановка задачи:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
а)

б)

в)

а) Вводим дополнительную фазовую переменную, таким образом, чтобы функционал был равен конечному значению фазовой переменной.


Запишем функцию Гамильтона:
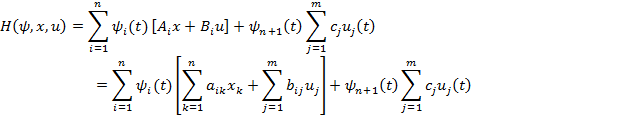
Запишем
функцию ![]() ,
которая является частью функции
Гамильтона, где управление присутствует
в явном виде:
,
которая является частью функции
Гамильтона, где управление присутствует
в явном виде:

![]()
![]()
![]()
![]()


𝝂j![]()
Найдем оптимальное управлении из условия максимизации функции Гамильтона:
![]()
Так как существуют ограничения на управление, то на ряду со стационарными точками необходимо проверить значения, которые достигает функция Гамильтона на границах:
0 uj Ujmax 𝜈j(t)>0 𝜈j(t)>0






![]()

Допустим 𝜈j имеет вид:
𝜈j(t)

t t1 t2 t3 t4
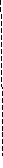



ujopt
Umax



t t1 t2 t3 t4


б) Вводим дополнительную фазовую переменную, таким образом, чтобы функционал был равен конечному значению фазовой переменной.


Запишем функцию Гамильтона:

![]()
Запишем
функцию ![]() ,
которая является частью функции
Гамильтона, где управление присутствует
в явном виде:
,
которая является частью функции
Гамильтона, где управление присутствует
в явном виде:
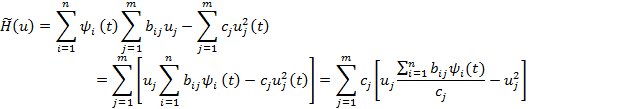

𝜈j(t)

![]()
![]()
uj 𝜈j/2 𝜈j/2 𝜈j/2 𝜈j/2 𝜈j(t) 𝜈j(t)














Решение линейных задач оптимального управления для экономических систем.
Оптимальное управление процессом фондообразования по критерию минимизации суммарного объема инвестирования
Исходная задача оптимального управления:
![]()
![]()

![]()
![]()
Перейдем к обобщенной задаче оптимального управления, которую приводим к универсальному виду:
Переобозначаем переменные:
![]()
Вводим дополнительную фазовую переменную, таким образом, чтобы функционал был равен конечному значению фазовой переменной.

![]()
![]()
![]()
Запишем функцию Гамильтона:
![]()
Запишем
функцию ![]() ,
которая является частью функции
Гамильтона, где управление присутствует
в явном виде:
,
которая является частью функции
Гамильтона, где управление присутствует
в явном виде:
![]()
Найдем оптимальное управление:
![]()
Запишем каноническую систему дифференциальных уравнений:
![]()
![]()
Условие трансверсальности:
=0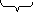
![]()
Краевая задача:

![]()




![]()
𝜓1(t)
1


t* T
t uopt
t T t* Imax



![]()
![]()
Рассмотрим отрезок временной оси

![]()
![]()
![]()
![]()
Рассмотрим временной период

![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
Тогда значение фондов в конечный момент времени равно
![]()
![]()
![]()
![]()
![]()
Из полученного уравнения выразим t*:
![]()
![]()
Определим минимальное значение функционала:
![]()
Оптимальное управление процессом фондообразования по критерию максимизации основных фондов
Задача оптимального управления:
![]()
![]()
![]()

![]() - ограничение на инвестиции
- ограничение на инвестиции
Переобозначаем переменные F и I:
![]()
![]()
Введем дополнительную фазовую переменную х2 таким образом, чтобы функционал был равен конечному значению фазовой переменной.

Запишем обобщённую задачу оптимального управления:

Запишем функцию Гамильтона:
![]()
Запишем
функцию ![]() ,
которая является частью функции
Гамильтона, где управление присутствует
в явном виде:
,
которая является частью функции
Гамильтона, где управление присутствует
в явном виде:
![]()
Найдем оптимальное управление:
![]()
Запишем каноническую систему дифференциальных уравнений:
![]()
![]()
![]()
![]()
![]()
Выражение для оптимального управления запишется следующим образом:
![]()
Построим график 𝜓1(t), где точка t* является точкой переключения управления:
t T t* 𝜓1(t)



-e-𝜇t
T t* C uopt Imax t











![]()
![]()
![]()
