12. Биномиальное распределение.

Пусть случайная величина X равна числу появлений события вn независимых испытаниях. Эта случайная величина может принимать одно из значений 0,1,2,…,n. Вероятности этих значений определяются по формуле Бернулли. Закон распределения дискретной случайной величины X задается таблицей

Этот закон называется биномиальным.

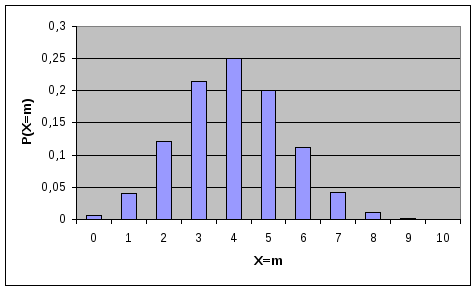
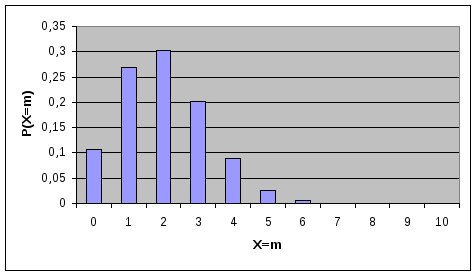
На рис.1 показаны вероятностиP(X=m) значений биномиального распределения при n=10, p=0,2 и p=0,4 соответственно.

Рис.1. Вероятности значений для биномиального распределения.

Для биномиального распределения ,.

Пример 2. Производится n=2 выстрела по цели. Вероятность попадания при каждом выстреле равна . Найти закон распределения случайной величиныX, равной числу попаданий в цель.

Может быть 0, 1 или 2 попаданий в цель. Вероятности этих значений определим по формуле Бернулли.

• Вероятность, что не будет ни одного попадания в цель .

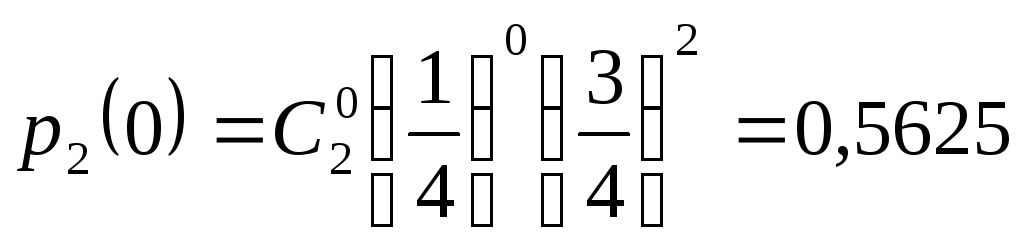• Вероятность, что будет одно попадание .

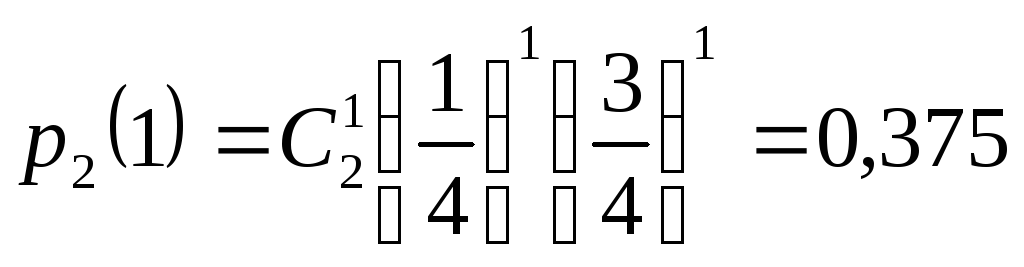• Вероятность, что будет два попадания .

Составим таблицу распределения случайной величины X

Заметим, что , поскольку все события, для которых определяются вероятности, являются несовместными и образуют полную группу.

13. Распределение Пуассона.

Случайная величина X имеет распределение Пуассона, если она принимает любые целые неотрицательные значения m=0,1,2,… с вероятностями

.

Число  называется параметром распределения Пуассона.

Таким образом,X может принимать счетное множество значений, и закон распределения этой случайной величины задается следующей таблицей

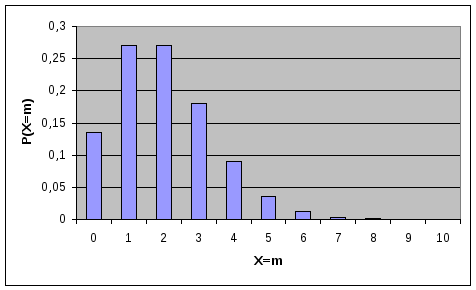
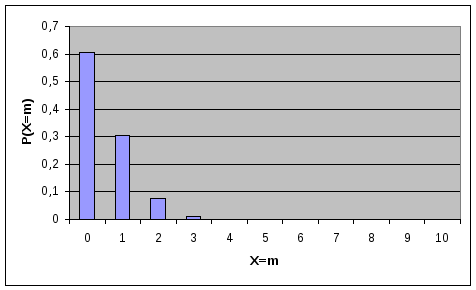
На рис.2 показаны вероятностиP(X=m) значений распределения Пуассона при =0,5 и =2 соответственно.

Рис.2. Вероятности значений для распределения Пуассона

Распределение Пуассона играет важную роль в физике, теории связи, теории надежности, теории массового обслуживания и т.д. - всюду, где в течение определенного времени может происходить случайное число каких-то событий: радиоактивных распадов, появления метеоритов, телефонных вызовов, помех в каналах связи, отказов оборудования, дорожных происшествий, несчастных случаев и т.д.

Распределение Пуассона является предельным для биномиального распределения, если в схеме Бернулли число испытаний n стремится к бесконечности, а вероятность p появления события в каждом испытании стремится к нулю, причем так, что. Отсюда получаем приближенную формулу

,

пригодную для практических расчетов. Этой формулой рекомендуется пользоваться, если , а.

Пример. Вероятность выпуска дефектного изделия равна . Из продукции выбраноn=5000 изделий. Найти вероятность того, что среди них окажется два или более дефектных изделия.

Параметр  равен . Определим требуемую вероятность

.

Так как , а , то искомая вероятность равна

.

При точных расчетах .

Для распределения Пуассона ,.

14. Геометрическое распределение.

Вероятность появления события в одном испытании равнаp. Производится серия из нескольких независимых испытаний, в каждом из которых может появиться или не появиться событие А. Испытания продолжаются до тех пор пока не появится событие . Случайная величинаX, равная числу испытаний до первого появления события , имеетгеометрическое распределение вероятностей.

Очевидно, что случайная величина X может принять одно из значений m=1,2,3,…. Значение X равно m, если в m-1-ом испытании событие не произойдет, а вm-ом испытании событие произойдет. Поэтому

.

Для геометрического распределения ,.