2. Действия над событиями.

Событие, состоящее в наступлении хотя бы одного из событий A или B, называется суммой событий A и B и обозначается A+B.

Событие, состоящее в наступлении обоих событий A и B, называется произведением событий A и B и обозначается AB.

Два события называются несовместными, если они не могут появиться вместе в результате одного испытания.

Пример 6. Событие A - выбор из ящика стандартной детали и событие B - выбор нестандартной детали несовместны.

Несколько событий образуют полную группу, если в результате испытания появится хотя бы одно из них.

Пример 7. Приобретено 2 лотерейных билета. Рассмотрим следующие события: H₁ - выигрыш выпал на оба билета, H₂ - выигрыш выпал только на первый билет, H₃ - выигрыш выпал только на второй билет, H₄ - выигрыш не выпал ни на один билет. Перечисленные события образуют полную группу несовместных событий. Такие события принято называть гипотезами.

Два несовместных события, образующих полную группу, называются противоположными. Для противополжных событий ивыполняются два условия:- достоверное событие,- невозможное событие.

События называются равновозможными, если есть основания считать, что ни одно из них не является более возможным, чем другое.

Появление того или иного числа очков на брошенной игральной кости - равновозможные события. Это верно в предположении, что игральная кость изготовлениа из однородного материала, имеет форму кубика и наличие очков не оказывает влияния на выпадение любой грани.

3. Вероятность события.

Вероятность - одно из основных понятий теории вероятностей. Существует несколько определений этого понятия. Приведем сначала, так называемое, классическое определение вероятности события. Рассмотрим пример.

Пример 8. Пусть в урне содержится 6 одинаковых перемешанных шаров, причем 2 из них - красные, 3 - синие и 1 - белый. Дадим количественную оценку возможности вынуть цветной шар из урны.

Испытание состоит в извлечении одного шара из урны. Каждый из возможных результатов испытания назовем элементарным исходом (элементарным событием). В примере возможны 6 элементарных исходов:

- появился красный шар,

- появился синий шар,

- появился белый шар.

Эти исходы образуют полную группу попарно несовместных событий, и они равновозможны.

Те элементарные исходы, в которых наступает интересующее нас событие, назовем благоприятствующими этому событию. Так событию A (появление цветного шара) благоприятствуют 5 исходов: . Следовательно, вероятность того, что выбранный наудачу шар окажется цветным, равна . Это число и дает количественную оценку возможности появления цветного шара.

Вероятностью события A называется отношение числа элементарных исходов, благоприятствующих этому событию, к общему числу всех равновозможных исходов испытания. Итак, вероятность события A определяется формулой

, (1)

где m - число элементарных исходов, благоприятствующих A, n - число всех возможных элементарных исходов испытания. Предполагается, что элементарные исходы несовместны, равновозможны и образуют полную группу. Определение вероятности события в соответствии с формулой (1) называется классическим.

Пример 9. Найти вероятность выпадения нечетного числа очков (событие A) при бросании правильной игральной кости. Общее число элементарных исходов равно 6, а число исходов, благоприятствующих событию A, равно 3. Поэтому .

Пример 10. Испытание состоит в подбрасывании двух правильных игральных костей. Найти вероятность, что сумма выпавших очков равна 10 (событие A). Все элементарные исходы имеют вид (i,j), где i,j=1,2,3,4,5,6. Общее число этих исходов равно n=36. Исходами, благоприятствующими событию A, являются (6,4), (5,5), (4,6), то есть m=3. Таким образом, .

Как и любая другая область математики теория вероятностей может быть построена на некоторой системе аксиом. Выбор системы аксиом должен быть таким, чтобы при этом были учтены наиболее важные случайные явления. Приведем аксиоматическое определение вероятности события, предложенное А.Н.Колмогоровым в 1933 г.

Обозначим через - пространство элементарных событий. Система аксиом, которые в совокупности определяют понятие вероятности, формулируется следующим образом.

Аксиома 1. Каждому случайному событию A ставится в соответствие неотрицательное число , называемое вероятностью.

Аксиома 2. .

Аксиома 3. Если события попарно несовместны, то.

Из этой системы аксиом следует, что

1. Для любого случайного события .

2. Вероятность невозможного события равна нулю.

3. Для любого события , где- противоположное событие.

Одним из недостатков классического определения вероятности является то, что оно неприменимо к испытаниям с бесконечным числом исходов. Этот недостаток можно преодолеть, если ввести геометрическое определение вероятности события.

Пусть на плоскости имеется область G и в ней содержится другая область g (рис.2).

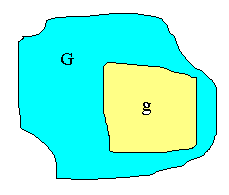
Рис.2. Геометрическое определение вероятности

Требуется найти вероятность события A, состоящего в том, что точка, взятая наудачу в области G, попадет в область g. Вероятность попадания точки в какую-либо часть области G пропорциональна мере (mes) этой части (длине, площади, объему и т.д.) и не зависит от ее расположения и формы:

.

Это есть геометрическое определение вероятности.

П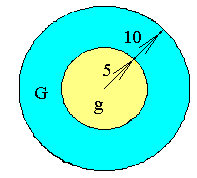ример 11. В круге радиуса 10 см. содержится круг радиуса 5 см. (рис.3). Найти вероятность, что точка, брошенная наугад в больший круг, попадет в круг меньшего радиуса (событие A). Предполагается, что вероятность попадания точки в плоскую фигуру пропорциональна площади этой фигуры и не зависит от ее расположения относительно большого круга.

Рис.3. Определение P(A)

Площадь большого круга равна , а площадь малого круга равна. На основании геометрического определения вероятности

.