2.2. Метод искусственного базиса

Если в исходной системе ограничений не выделен допустимый базис, как того требует алгоритм симплекс-метода, для его нахождения можно решить вспомогательную задачу, которая ставится сле-

дующим образом.

Пусть исходная система нетривиальных ограничений задана в общем виде

a11x1 + a12 x2 + +a1n xn = b1,a21x1 + a22 x2 + +a2n xn = b2 ,

........................................

am1x1 +am2 x2 + +amn xn = bm ,

где bi ≥ 0,i =1, ,m. Выполнения последнего условия всегда можно

добиться, умножив уравнения на −1. Введем в систему новые (искусственные) переменные y1, y2 , , ym

a11x1 + a12 x2 + + a1n xn + y1 = b1,a21x1 + a22 x2 + + a2n xn + y2 = b2 ,

........................................

am1x1 +am2 x2 + + amn xn + ym = bm ,

Если последняя задача имеет решение, то возможны два случая:

47

1. Если min F > 0, то система ограничений не имеет допустимого базиса и задача не имеет решений.

2. Если min F = 0, то система ограничений имеет неотрицательное базисное решение. Чтобы получить систему ограничений, эквивалентную исходной, но с выделенным допустимым базисом, необходимо, чтобы в заключительной симплекс-таблице все искусст-

венные переменные были свободными. Пример 3.2. Решить задачу

z = x1 +3x2 +8 → min−x + x + x =1,

1 2 3

x1 +3x2 − x4 =19,

3x1 + x2 + x5 = 33,

x ≥ 0

симплекс-методом.

Решение. В данной задаче допустимый базис выделен лишь частично (переменные x3 , x5 ), поэтому ограничимся лишь введением одной искусственной переменной y и решим следующую задачу

сем в таблицу строку для функции z , одновременно преобразуя и ее. Получим

Сделаем шаг симплекс-метода с выделенным разрешающим элементом

48

Выводим из базиса переменную y и вводим в базис x1 .

Вспомогательная задача F → min решена и искусственная переменная y – свободная. Поэтому опускаем последнюю строку и столбец, и получаем симплекc-таблицу для исходной задачи с выделенным допустимым базисом:

Более того, данная симплекc-таблица – заключительная, поэтому решением задачи является X1 = (4,5,0,0,16), а так как имеется свобод-

ный столбец x3 с нулевой оценкой, то у задачи есть альтернативное решение. Выводим из базиса переменную x5 и вводим в базис x3 :

49

иполучаем альтернативное решение X2 = (10,3,8,0,0) . Поэтому общее решение задачи

X = (1−t)X1 +tX2 = (1−t)(4,5,0,0,16)+t (10,3,8,0,0)=

=(4 +6t,5 −2t,8t,0,16 −16t),t [0,1]

иzmin = z (X * )= 27 .

Пример 3.3. Решить задачу

50

Все элементы строки оценок для задачи F → min отрицательны, поэтому симплекс-таблица – заключительная, но, так как min F = 9 / 2 > 0, то исходная задача не имеет ни одного допустимого базиса и решений не имеет.

Задачи для самостоятельного решения

Решить задачи линейного программирования, используя метод искусственного базиса

51

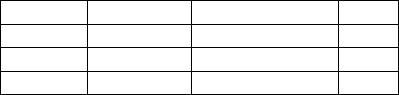
51. Суточная потребность человека в витаминах и минеральных веществах удовлетворяется за счет потребления двух продуктов – киви и гранатов. Содержание питательных веществ в продуктах (мг/100 г), суточные нормы их потребления (мг) и цена продуктов (руб. за 100 г) задаются таблицей

При этом гранат должно быть не более 800 г. Составить математическую модель задачи и найти суточный рацион минимальной стоимости.

52