6. Элементы теории расписания.

Это раздел дискретной математики, занимающийся проблемами упорядочения. В общем случае формулировка основной задачи ТР имеет следующий вид: дано некоторое множество работ или требований J=(J1, J2, ..., Jn). Этот вектор характеризуется длительностью обработки требований, стоимостью обработки требований, моментами поступления требований и дириктивными сроками окончания обслуживания требований. Задано некоторое множество машин или приборов М=(M1, M2, ..., Mm). Ставится задача дискретной оптимизации, т.е. построить расписание, минимизирующее время выпонения работ.

Расписание - указание, на каких машинах и в какое время долны обслуживаться требования.

Задачи ТР можно разделит на 2 группы:

1) задачи с прерыванием. В любой момент обслуживанея требования на машине может быть прервано ради обслуживания другого требования.

2) задачи без прерывания. В этом случае каждые требованияна машине обслуживаются от начала до конца без прерываний.

По дисциплине выполненияс работ на машине можно выделить 4 класса задач:

1) задачи открыты линий. Для каждого требования задано свое подмнодество машин, на каждой из которых оно должно обслуживаться некоторое время, порядок обслуживания произвольный и задаются разнооьразные целевые функции.

2) раьочий цех. Для каждого требования задается свое упорядоченное подмножество машин, которым оно должно обладать в заданном порядке.

3) потоковая линия. Все машины упрядочены и каждое требование проходит эти машины в том же порядке.

4) задачи с директивными строками. Для каждого требования задан момент поступления, время обслуживания и директивный срок окончания обслуживания. Порядок обслуживания на машинах произвольный.

7. Потоковая линия. Алгоритм Джонсона.

потоковая линия — все машины упорядочены - M=(M1,М2,Мn) и каждое требование проходит все машины в этом порядке. Расписание задано перестановкой требований. Как правило, минимизируется общее время обслуживания требований.

Алгоритм Джонсона позволяет найти кратчайшие пути между всеми парами вершин взвешенного ориентированного графа. Применяется для составления расписания на двух машинах. Для решения данного алгоритма используются следящие требования.

1.Все треб. должны пройти обработку последовательно на всех машинах.

2.Любая машина в каждый момент времени может обрабатывать одно требование.

3.Не допускается прерываний при обслуживание требований, и след решение определяется некоторой перестановкой требований.

Рij-время обслуживания требования i,на машине j

1.Сmax-время окончания обслуживания послед требования на послед машине.

n

2.Σ сj-сумма времени окончания обслужив требований на машине n.

i=1

8. Неориентированные графы. Основные понятия: вершины и их степень, ребра, кратные ребра, петли. Матрица смежности неориентированного графа. Примеры.

Неориентированный граф  — это упорядоченная пара, для которой выполнены следующие условия:

• — это непустое  вершин, или узлов,

• — это множество пар (в случае неориентированного графа — неупорядоченных) вершин, называемых рёбрами.

Вершины и рёбра графа называются также элементами графа, число вершин в графе — порядком, число рёбер — размером графа.

Два ребра называются кратными, если множества их концевых вершин совпадают. Ребро называется петлёй, если его концы совпадают.

Степенью вершины называют количество инцидентных ей рёбер (при этом петли считают дважды).

Пусть есть граф с n вершинами, пронумерованными числами от 1 до n. Составляется матрица A размера n x n со следующими правилами для элементов. I. Если элемент не на диагонали, то элемент (i, j) равен: a) 1, если вершины i и j соединены ребром; b) 0, если условие a не выполнено. II. Если элемент на диагонали (i=j), он равен единице, если вершина i имеет петлю (дугу или ребро с исходом и заходом в одну и ту же вершину), и 0, если петли нет. Эта матрица и называется матрицей смежности.

Пример 1.

x1 x2 x3 x4 x5 x6 x7 x8 x1 2 0 0 0 1 0 1 0 x2 0 0 1 0 0 1 1 0 x3 0 1 0 1 0 1 0 0

x4 0 0 1 0 1 0 0 0 x5 1 0 0 1 0 0 0 1 x6 0 1 1 0 0 0 0 0 x7 1 1 0 0 0 0 0 0 x8 0 0 0 0 1 0 0 0

Пример 2.

1 2 3 4 5 6 7

1 0 1 1 0 1 0 0

2 1 0 0 1 0 1 0

3 1 0 0 1 1 0 0

4 0 1 1 0 0 1 0

5 1 0 1 0 0 0 1

6 0 1 0 1 0 0 1

7 0 0 0 0 1 1 0

Номера столбцов и строк соответствуют номерам вершин. На пересечении соответствующей строки и столбца стоит единица, если между вершинами с теми же

номерами имеется одно ребро. Если две вершины соединены несколькими ребрами, то

ставится число равное количеству таких ребер.

9. Инцидентность. Матрица инцидентности неориентированного графа. Примеры.

Матрицей инцидентности ориентированного (или неориентированного) графа G=(V,E) с n вершинами V= { v₁, … , v_n} и m ребрами E={e₁, …, e_m} называется матрица B_G размера n × m с элементами

Таким образом, в матрице инцидентности B_G любому ребру e_j = (v_i,v_k) соответствует j-ый столбец, в котором в i-ой строке стоит 1, а в k-ой - -1. Ребра-петли выделяются числом 2. Для проверки наличия ребра между двумя вершинами v_i и v_k требуется просмотреть i-ю и k-ую строки B_G, поиск всех соседей вершины требует просмотра соответствующей строки. Если m >> n, то это требует существенно больше времени, чем при использовании матрицы смежности. Поэтому при практическом решении задач на графах матрица инцидентности почти не используется.

Матрица инцидентности

10. Ориентированные графы. Матрица инцидентности орграфа. Примеры.

Направленные ребра графа, т.е. ребра, для которых определены вершины, из которых они выходят, и вершины в которые входят, называются дугами.

Если все ребра графа направлены , то он называется ориентированны или орграфом.

Матрицей инцидентности орграфа G(V,E) называется матрица B(G)размера (n – число вершин, m – число ребер) с элементами.

11. Матрица смежности орграфа. Примеры.

12. Подграфы. Полные графы. Клики. Примеры.

Граф  называется подграфом графа , если  и  являются подмножествами R и , причем ребро содержится в  только в том случае, если его концевые вершины содержатся в .

        Пусть       –   некоторое    подмножество    множества    вершин    графа 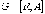 и пусть – множество всех ребер графа G, концевые вершины которых входят в . Тогда граф  называется вершинно-порожденным подграфом графа G. Обозначим через  некоторое подмножество множества ребер графаG и пусть  есть множество всех вершин графа G, инцидентных ребрам из . Тогда граф  называется реберно-порожденным подграфом  графа G.

 Рисунок 14.3.

        На рис. 14.3 изображены вершинно-порожденный подграф , представленного на рис. 11.1 (множество вершин ), и реберно–порожденный подграф  того же графа G (того же графа G ( множество ребер ).

Полный граф — простой граф, в котором каждая пара различных вершин смежна. Полный граф с  вершинами имеет  рёбер и обозначается . Является регулярным графом степени .

Полный ориентированный граф - это ориентированный граф, в котором каждая пара различных вершин соединена парой дуг (с различными направлениями).

Графы с  по  являются планарными. Полные графы с большим количеством вершин не являются планарными, так как содержатподграф  и, следовательно, не удовлетворяют критерию Понтрягина-Куратовского.

Примеры[править | править исходный текст]

Ниже приведены полные графы с числом вершин от 1 до 12 и количества их рёбер.

K1: 0	K2: 1	K3: 3	K4: 6
K5: 10	K6: 15	K7: 21	K8: 28
K9: 36	K10: 45	K11: 55	K12: 66

Кликой в неориентированном графе G = (V, E) называется подмножество вершин C ⊆ V, такое что для любых двух вершин в C существует ребро их соединяющее. Это эквивалентно утверждению, что подграф, порождённый C является полным.

Наибольшая клика – это клика, которая не может быть расширена путём включения дополнительных смежных вершин, то есть нет клики большего размера, включающей все вершины данной клики.

Максимальная клика – это клика максимального размера для данного графа. Кликовое число ω(G) графа G - это число вершин в максимальной клике графа G. Число пересечений^[en] графа G – это наименьшее число клик, вместе покрывающих все рёбра графа G.

Противоположное клике понятие – это независимое множество в том смысле, что каждая клика соответствует независимому множеству в дополнительном графе. Задача о покрытии кликами^[en] состоит в нахождении как можно меньшего числа клик, содержащих все вершины графа. Связанный термин – это биклика, полный двудольный подграф . Двудольная размерность^[en] графа – это минимальное число биклик, необходимых для покрытия всех рёбер графа.