
Методичка по матану (1)
.pdfМинистерство образования и науки Российской Федерации
ФЕДЕРАЛЬНОЕ ГОССУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«КАЗАНСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ им. А.Н. ТУПОЛЕВА-КАИ»
С.И. ДОРОФЕЕВА
Приближенное решение уравнений. Исследование функций и построение графиков
Учебное пособие
Рекомендовано к печати Учебно-методическим центром КНИТУ-КАИ
Казань 2012
УДК 517
Доро 69
Рецензенты:
докт. физ.-мат. наук, проф. С.Р. Насыров (Казанский государственный университет);
докт. физ.-мат. наук, проф. Ф.Н. Гарифьянов (Казанский государственный энергетический университет)
Доро 69 Дорофеева С.И. Приближенное решение уравнений. Исследование функций и построение графиков. Казань: Изд-во Казан. гос. техн. ун-та, 2012. 40 с.
ISBN 978-5-7579-1108-3
Пособие охватывает учебный материал, соответствующий действующей программе по математике для технических вузов.
Приведены методы приближенного решения уравнений и основные теоретические сведения, необходимые для исследования функций.
Предлагается 30 вариантов заданий для индивидуальной самостоятельной работы студентов. Даются практические рекомендации к выполнению задания. Подробно рассматривается решение типового варианта.
Предназначаются для студентов 1-го курса инженерно-технических специальностей всех форм обучения.
Табл. 3 Ил. 18 Библиогр.: 5 назв.
УДК 517
|
© |
Изд-во Казан. гос. техн. ун-та, 2012 |
ISBN 978-5-7579-1108-3 |
© |
С.И.Дорофеева, 2012 |
Введение
Многие задачи науки и техники, как известно, приводят к исследованию
функциональных зависимостей (функций). Исследовать заданную функцию
y f x с областью определения X – это значит изучить ее поведение при изме-
нении независимой переменной x X . Применение дифференциального исчисле-
ния к изучению функцией является одним из самых важных приложений диффе-
ренциального исчисления.
При исследовании функций часто используют ее наглядное геометрическое изображение. Такое представление особенно полезно при обсуждении качествен-
ных вопросов поведения функций. График функции (множество точек на плоско-
сти с координатами x, f x , x X в декартовой системе координат xOy) на-
глядно иллюстрирует изменения функции, ее характерные свойства и особенно-
сти. В некоторых случаях график удобнее строить в полярной системе координат.
При построении графиков функций ó f x необходимо знать с требуемой точ-
ностью точки пересечения графиков функций с осями координат, т.е. решать уравнения f 0 y0 и f x 0.
Цель работы – помочь студентам: 1) научиться исследовать функции, задан-
ные аналитически; 2) строить графики этих функций; 3) находить, пользуясь дифференциалом, приближенные значения функции; 4) аппроксимировать (ло-
кально, в окрестности данной точки) наилучшим образом заданную функцию по-
линомами (первой степени, второй степени, …, n–й степени).
Постановка задач индивидуального задания
Каждый из вариантов индивидуального задания предполагает ознакомление с необходимым теоретическим материалом, решение вычислительных задач, про-
ведение исследования функций и построения графиков.
Содержание задания:
1.Найти корень уравнения (решить уравнение).
а) Отделить корень графически и найти его методом половинного деления
(метод проб, метод «вилки») с точностью до 0,01.
|
б) Комбинированным методом хорд и касательных найти один из корней |
уравнения вида ax3 bx2 cx d 0 с точностью до 0,001. |
|
2. |
Исследовать заданную функцию y f x и построить ее график. |
3. |
Найти наибольшее и наименьшее значения (глобальные максимум и ми- |
нимум) заданной непрерывной функции y f x на данном отрезке a,b .
4.Вычислить приближенное значение заданной функции y f x в данной точке x x1, пользуясь дифференциалом функции.
5.Найти полиномы Тейлора первой T1 x и второй T2 x степеней для за-
данной функции y f x в данной точке x0; построить в окрестности этой точки фрагменты графиков функции y f x и аппроксимирующих ее полиномов y T1 x , y T2 x .

МЕТОДЫ ПРИБЛИЖЕННОГО РЕШЕНИЯ УРАВНЕНИЙ И ИССЛЕДОВАНИЕ ФУНКЦИЙ
Решение первой задачи
Найдем корень, используя приближенное решение уравнений. Точные реше-
ния уравнения f x 0 не всегда могут быть найдены. Будем искать действитель-
ные значения корней с помощью численных методов при заданной точности.
Решение состоит из двух этапов:
1)отделение корней, т.е. определение отрезков, внутри которых находится только один корень;
2)уточнение корней до заданной степени точности.
Отделение корней можно провести графически или аналитически, учитывая,
что если непрерывная монотонная функция на концах малого отрезка a;b прини-
мает значения разных знаков, то внутри этого отрезка содержится корень уравне-
ния f x 0. Для решения уравнений, содержащих тригонометрические, лога-
рифмические, показательные функции, удобно пользоваться таблицами математи-
ческих справочников [1].
Метод половинного деления. |
Пусть корень уравнения f x 0 отделен и |
||
находится на отрезке a;b . Точка x |
|
a b |
– середина отрезка разбивает отрезок |
|
|||
1 |
2 |
|
|
на два равных: a;x1 и x1;b .
Из этих отрезков выбираем тот, на концах которого функция f x принима-
ет значения разных знаков и также делим его пополам. Процесс деления пополам продолжается до тех пор, пока не получится отрезок an;bn , длина которого
b a меньше заданной точности ε. 2n
Окончательно за приближенное значение корня принимают число an bn .
2
5

Погрешность не превышает |
b a |
. |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
2n 1 |
|
|
|
|
|
|
|
|
Пример. Решить с точностью до 0,01 уравнение x ex 0. |
|
|
|||||||||||||||
Решение. Найдем интервал изоляции корня графически. Уравнение |
|
|
|||||||||||||||
|
|
|
|
|
|
|
y |
|
x e |
x |
0 запишем в виде e |
x |
x, где f1 x e |
x |
, |
||
|
|
|
|
|
|
|
|
y ex |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
f2 x x. Абсцисса точки пересечения графи- |
|
|||||||
y x |
ков |
f1 x и |
f2 x – корень уравнения |
|
|
||||||||||||
1 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f x x ex; за интервал изоляции возьмем от- |
|
|||||||
|
|
|
|
|
|
|
Рис. 1 |
резок 1;0 |
(видно по рис. 1): |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
f 1 1 1 0,632; f 0 1. e
Середина отрезка: 1 0 0,5; f 0,5 0,5 0,606 0,106. 2
Отрезок |
a ;b |
1; 0,5 , |
его |
середина |
1 0,5 |
0,75; |
|
|
|||||||
|
1 |
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
f 0,75 0,75 0,472 0,278.
Отрезок |
a ;b |
0,75; 0,5 , середина отрезка |
|
0,75 0,5 |
|
0,625; |
|||
|
|
||||||||
|
2 |
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||
f 0,625 0,625 0,538 0,087. |
|
|
|
|
|
|
|||
Отрезок |
a3;b3 0,625; 0,5 , |
середина |
|
отрезка |
|
0,5625; |
|||
f 0,562 0,562 0,571 0,008. |
|
|
|
|
|
|
|||
Отрезок |
a ;b 0,625; 0,562 ; |
середина |
0,625 0,562 |
|
0,594; |
||||
|
|
|
|
||||||
|
|
4 |
4 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||
f 0,594 0,594 0,554 0,04 и a5;b5 0,594; 0,562 .
Длиной отрезка a4;b4 будет 0,594 0,562 0,032 ε, поэтому продолжим
деление и найдем середину отрезка: 0,594 0,562 0,578.
2
Значение функции: f 0,578 0,578 0,5599 0,018.
6

Отрезок |
a6;b6 0,578; 0,562 , |
середина |
0,578 0,562 |
0,57; |
|
2 |
|||||
|
|
|
|
f 0,57 0,57 0,565 0,005; a7;b7 0,57; 0,562 , длина отрезка a7;b7
равна 0,008 ε.
За приближенное значение корня берем середину этого отрезка: ξ 0,566 с
учетом заданной точности ξ 0,57.
Способы уточнения корней на отрезке a;b предполагают, что для функции f x выполняются условия:
1)f x непрерывна на a;b вместе с производными первого и второго
порядков; |
|
|
|
2) |
значения f x на |
концах |
отрезка a;b имеют разные знаки, т.е. |
f a f b 0; |
|
|
|
3) |
производные f x |
и f x |
сохраняют знак на a;b . |
Условия 1 и 2 гарантируют, что на a;b находится хотя бы один корень, а из условия 3 следует, что на данном интервале функция монотонна и поэтому корень будет единственным.
Далее будем предполагать, что условия 1–3 выполняются.
Метод хорд. Метод заключается в многократном процессе замены кривой хордой и отыскания точки пересечения хорды с осью абсцисс (рис. 2).
y
y f x
B
a |
x1 |
x |
|
|
x |
b |
A1 |
|
A |
|
Рис. 2 |
|
Пусть корни уравнения f x 0 отделены и выбран отрезок a;b . Пусть x –
точное значение корня.
7

Уравнение прямой, проходящей через точки A a; f a и B b; f b : |
|
||||
|
x a |
|
y f a |
|
|
|
|
|
. |
(*) |
|
|
b a |
f b f a |
|||
Уравнение оси абсцисс: |
|
|
|
|
|
|
|
y 0. |
(**) |
||
Точку x1 найдем из системы уравнений (*) и (**):
b a f a
x1 a f b f a
для f x 0, |
f x 0 |
или f x 0, |
f x 0; |
b a f b
x1 b f b f a
для f x 0, f x 0 или f x 0, f x 0;
x x |
b xk 1 f xk 1 . |
|
k k 1 |
f b f x |
|
|
k 1 |
|
Последовательность a, x1, x2 , …, xk ,… стремится к искомому корню урав-
нения f x 0.
Вычисления ведутся до тех пор, пока не перестанут изменяться те десятич-
ные знаки, которые нужны для реализации заданной степени точности вычисле-
ний.
Оценка погрешности:
|
|
|
|
|
x |
ξ |
|
|
f a f b |
max |
|
f |
|
x |
|
|
, |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
f x 3 |
||||||||||
|
|
|
|
|
|
2 |
a x b |
|
|
||||||||
|
|
|
|
||||||||||||||
где |
x |
– точное значение корня; ξ – приближенное значение корня. |
|||||||||||||||
|
Пример. Найти один положительный корень |
уравнения (с точностью |
|||||||||||||||
до 0,01): |
|
|
|
|
|
|
|
|
|||||||||
f x x3 2x2 3x 5 0.
8

Решение. Определим знаки f x |
в различных точках: |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
0 |
|
|
1 |
|
|
1,5 |
|
1,8 |
|
|
1,9 |
|
|
2 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f x |
|
– |
|
|
– |
|
|
– |
|
– |
|
|
+ |
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
Выберем интервал 1,8;1,9 и применим метод хорд: |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f 1,8 0,248 и f |
1,9 0,339. |
|
|
|
|
|
|
|
|
||||||||||||||||||||
Тогда |
|
x 1,9 1,9 1,8 0,339 |
|
1,842; |
|
|
f 1,842 0,01009 0. |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
0,339 0,248 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Следовательно, 1,842 ξ 1,9. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 1,9 |
|
|
0,058 0,339 |
1,8437. |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
0,339 0,01009 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
За значение корня примем ξ 1,84, так как два знака после запятой (заданная |
||||||||||||||||||||||||||||||||||||||||||||||||||||
точность 0,01) при переходе от x1 |
к x2 сохраняются. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
Метод касательных (метод Ньютона). Действительный корень изолирован на |
||||||||||||||||||||||||||||||||||||||||||||||||||||
отрезке a;b и условие 1 для f x выполнено. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
Возьмем на отрезке a;b такое числоx0, что |
|
|
f x0 f x0 0. Обычно за x0 |
|||||||||||||||||||||||||||||||||||||||||||||||||
берут x a или x b (рис.3). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
В точке M0 b; f b строим касательную. За приближенное значение корня |
||||||||||||||||||||||||||||||||||||||||||||||||||||
берем абсциссу точки пересечения касательной и оси Ox. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M0 |
|
|
|
|
|
Уравнение касательной: |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y y0 |
f x0 x x0 . |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M1 |
|
|
|
|
|
|
|
|
Решая систему |
|
|
y y |
f |
|
x |
x x , |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
на- |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y 0, |
|
|
|
|
|
|
|||
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
x |
|
|
ходим |
|
|
точку x1; |
f x1 , |
где x1 |
– первое при- |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b x |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
y f x |
|
|
|
|
|
|
|
|
|
|
ближение корня x |
|
x |
f x0 |
. |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f x0 |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
0 |
|
|
|
|
|
|
||||||
Продолжая этот процесс, найдем x2 , x3, …, xk , … Полученная последова- |
||||||||||||||||||||||||||||||||||||||||||||||||||||
тельность сходится к искомому корню: |
|
|
x |
|
x |
|
|
|
|
f xn 1 |
|
, n 2,3,... |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
f xn 1 |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
n 1 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Оценка погрешности:
|
|
|
f ξ 2 |
|
f x |
|
|
x |
ξ |
|
max |
|
. |
||
|
|
|
|
||||
|
f x |
|
|||||
|
|
2 |
a x b |
3 |
|||
|
|||||||
|
|
|
|
|
|
|
|
Замечание. На каждой итерации объем вычислений в методе касательных больше, чем в методе хорд, так как приходится вычислять не только f x , но и f x , зато сходимость метода значительно выше. На практике чаще всего при-
меняют комбинированный метод (хорд и касательных).
Комбинированный метод. Ограничения, наложенные на функцию f x ,
сохраняются: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) a;b – отрезок изоляции корня; |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
б) |
функция f x |
непрерывна |
на |
a;b |
вместе |
со своими производными |
|||||||||||||||||
f x и f x ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в) для x a;b |
f a f b 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
г) |
f x и f x |
сохраняют знак на a;b . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
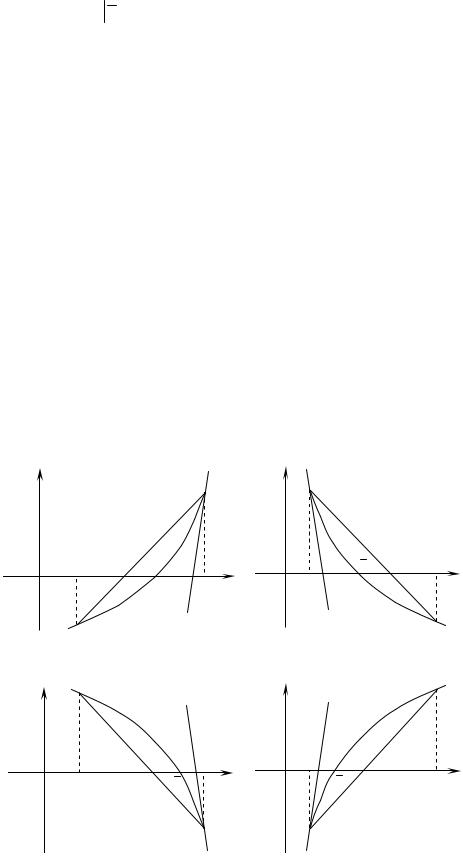
|
|
|
f b f b 0 B |
|
|
|
A |
|
f a f a 0 |
|
|||||||||||||
|
y 0 |
|
|
|
|
|
|
|
|
|
|
y 0 |
|
|
|
|
|
|
xхорд |
|
|||
|
|
a |
|
|
|
|
|
|
|
|
|
y 0 |
|
|
|
|
|
x |
b |
||||
|
y 0 |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
a |
x1кас |
|
|
|
|
1 |
|
|
||||||
|
|
|
хорд |
|
кас |
b |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
x1 |
|
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
A |
|
y f x |
|
|
|
|
|
|
|
|
|
|
|
y f x |
|
B |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
|
|
|
|
||
|
A |
|
y f x |
|
|
|
|
|
|
|
|
|
|
y f x |
|
B |
|||||||
|
y 0 |
|
|
|
|
|
|
|
|
|
|
y 0 |
|
xкас |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
кас |
y 0 |
a |
|
|
|
|
|
|
|
||||
|
y 0 |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||
|
|
a |
|
хорд |
|
x |
|
1 |
|
|
|
x |
|
|
xхорд |
|
|
|
b |
||||
|
|
x |
|
|
|
b |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f b f b 0 |
|
|
|
|
B |
|
|
A |
f a f |
|
a |
0 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
г |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
