
Методичка по матану (1)
.pdf
Если |
y 0, |
y 0 |
или |
y 0, |
y 0, |
то |
a x1хорд |
x |
x1кас b |
(рис. 4, а и 4, б). |
|
|
|
|
|
|
|
|
|
Если |
y 0, |
y 0 |
(рис. |
4, в) |
или |
y 0, |
y 0 (рис. 4, г), |
||
то a x1кас x x1хорд b.
Во всех случаях истинный корень уравнения заключен между приближенны-
ми корнями, полученными методом хорд и методом касательных.
Пример. Найти значение положительного корня уравнения x4 2x 4 0 с
точностью 0,01 комбинированным методом.
Решение. Найдем интервал изоляции корня графически: x4 2x 4, корни
принадлежат отрезкам 2; 1 и 0;2 (рис.5).
y
y x4 |
8 |
|
y 2x 4 |
|
4 |
|
|
-2 |
0 |
2 |
x |
Рис.5
Проверим: f 0 4; |
f 2 8; при x 1 |
|
|
|
|
|
|
|
|
x |
f 1,7 0,952. |
|||||
|
f 1 5; при x 1,7 |
|||||||||||||||
Примем за отрезок изоляции отрезок 1; 1,7 : |
|
|
|
|
||||||||||||
f x 4x3 2; |
f x 12x2 |
0 для любого x. |
|
|||||||||||||
Значение функции |
f 1.7 0, поэтому xкас |
|
1,7; |
|
||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
xкас |
1,7 |
|
0,952 |
|
|
1,7 |
|
0,952 |
1,646; |
|
||||||
|
|
|
|
|
|
|||||||||||
1 |
|
|
4 1,7 3 2 |
|
|
|
|
17,652 |
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
1,7 1 |
|
f |
1 |
|
|
|
||||
a 1; |
xхорд 1 |
|
|
|
|
|
|
|
|
1,588. |
|
|||||
f |
1,7 |
|
f |
1 |
|
|||||||||||
|
|
1 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вычислим f 1,646 0,048; f 1,646 15,838; f 1,588 0,817 0.
Проведем вычисления на отрезке [1,588; 1,646].
11

x2кас 1,646 0,048 1,643; 15,838
xхорд |
1,588 1,7 1,588 f 1,588 |
1,639. |
||||||||
2 |
f 1,7 |
f 1,588 |
|
|
|
|||||
|
|
|
|
|||||||
Вычислим f 1,639 0,051 0; f |
1,643 0,004; |
f 1,643 15,740. |
||||||||
Проведем вычисления на отрезке [1,639; 1,643]. |
|
|
|
|||||||
|
xкас 1,643 |
0,004 |
|
1,6427; |
||||||
|
|
|
||||||||
|
3 |
15,740 |
|
|
|
|
||||
|
|
|
|
|
|
|||||
xхорд 1,639 1,7 1,639 f 1,639 |
1,642. |
|||||||||
3 |
|
|
|
|
f |
|
|
|
|
|
f 1,7 |
|
1,639 |
|
|
||||||
За приближенное значение корня примем ξ 1,64.
Решение второй задачи.
Исследование заданной функции y f x и построение ее графика рекомен-
дуется проводить по следующей общей схеме:
1. Провести элементарное исследование функции:
1.1.Установить область определения (существования) функции.
1.2.Установить, является ли функция четной, нечетной, периодической (спе-
цифические особенности функции позволяют сократить объем исследований). 1.3. Найти точки разрыва функции, если они существуют, и установить про-
межутки непрерывности.
1.4.Установить поведение функции в окрестностях точек разрыва и наличие
уграфика функции вертикальных асимптот.
1.5.Найти точки пересечения (если они существуют) графика функции с осями координат (методами приближенного вычисления корней).
1.6. Установить поведение функции в бесконечности, т.е. при x и x (для неограниченной области определения функции).
1.7. Установить наличие у графика функции наклонных (в частности, гори-
зонтальных) асимптот и (в случае их существования) найти их. 2. Исследовать функции с помощью производных:
12
2.1.Установить промежутки монотонности (возрастания, убывания) функции. 2.2. Найти точки внутренних локальных экстремумов (точки максимума,
точки минимума, если они существуют) и экстремальные значения функции.
2.3. Установить интервалы выпуклости и вогнутости функции, если они су-
ществуют.
2.4. Найти точки перегиба функции (если они существуют) и значения функ-
ции в этих точках, а также угловые коэффициенты касательных к графику в точ-
ках перегиба графика функции.
3. Построить (в целом) график функции.
При выполнении п.1.1 надо воспользоваться определением области опреде-
ления функции, заданной аналитически, т.е. формулой (или формулами). Обла-
стью определения называют множество действительных значений аргумента, при которых формула, определяющая функцию, имеет смысл, причем как в процессе всех необходимых вычислений по этой формуле, так и в окончательном результа-
те для функции получаются действительные значения.
При выполнении п.1.2 надо воспользоваться свойствами функции.
- Четной (нечетной) называют функцию y f x , если она определена на сим-
метричном относительно нулевой точки множестве X и для любого x X вы-
полняется равенство
f x f x f x f x .
- Если функция y f x , |
x X четна, то ее график симметричен относительно |
оси ординат. |
|
- Если функция y f x , |
x X нечетна, то ее график симметричен относительно |
начала координат.
- Если функция четна или нечетна, то исследование можно проводить для x 0, и отображать соответствующим образом на левую полуплоскость.
- Периодической называют функцию y f x , x R R , , если для нее существует такое положительное число T , называемое периодом, что для любого x R справедливо равенство f x T f x .
13
- Если функция f x является периодической с периодом T , то для построения ее графика достаточно знать ее график на одном из промежутков вида a x a T ; смещая этот график вдоль оси абсцисс на отрезки T , 2T , …, по-
лучают график функции y f x .
При выполнении п.1.3 надо воспользоваться определениями и теоремой: - Функция f x непрерывна в точке x x0, если lim f x f x0 .
-Непрерывной в интервале называют функцию, непрерывную в каждой точке этого интервала.
-Точками разрыва функции y f x , x X , называют точки, в которых наруше-
но условие непрерывности: |
|
|
|
|
|
|
||||
|
если |
lim |
f x |
lim |
f x f x0 , то x0 – точка непрерывности; |
|||||
|
|
x x0 0 |
|
x x0 0 |
|
|
|
|
|
|
|
если |
lim |
f x |
lim |
f x f x0 , то |
x0 |
– точка разрыва первого рода |
|||
|
|
x x0 0 |
x x0 0 |
|
|
|
|
|
||
(точка устранимого разрыва); |
|
|
|
|
|
|
||||
|
если |
lim |
f x |
lim |
f x , то x0 – точка разрыва первого рода, функция |
|||||
|
|
x x0 0 |
|
x x0 0 |
|
|
|
|
|
|
в точке x0 |
имеет скачок |
f x0 |
0 f x0 0 ; |
|
|
|
||||
если хотя бы один из пределов |
lim |
f x или lim |
f x не существует |
|||||||
|
|
|
|
|
|
x x0 0 |
|
x x0 0 |
||
или равен бесконечности, то в точке x0 |
функция имеет разрыв второго рода. |
|||||||||
|
Любая элементарная функция непрерывна в каждой точке ее области опреде- |
|||||||||
ления. |
|
|
|
|
|
|
|
|
|
|
|
При выполнении п.1.4 надо воспользоваться определением: прямую x a |
|||||||||
(a – предельная точка |
X ) называют вертикальной (параллельной оси Oy) |
|||||||||
асимптотой графика функции y f x , x X , если |
|
|||||||||
|
|
|
lim f x |
или |
lim |
f x . |
||||
|
|
|
x a 0 |
|
|
|
x a 0 |
|
|
|
|
При выполнении п.1.5 надо решить уравнения |
f x 0 |
и y f 0 , действи- |
|||||||
тельные корни которых и будут точками на осях Ox и Oy, через которые прохо-
14
дит график функции y f x . Действительные (вещественные) корни уравнения f x 0 называют нулями функции. Уравнение y f x можно решить одним из
рассмотренных методов приближенного решения уравнения.
В простейших случаях область определения функции может быть разбита точками разрыва и нулями функции на определенное число интервалов, в которых
f x сохраняет знак ( f x 0 или f x 0). |
|
|
При выполнении п.1.6 надо для f x , |
x R, найти пределы |
lim f x и |
x
lim f x .
x
При выполнении п.1.7 надо воспользоваться определениями асимптот функ-
ции.
- Прямые y k1x b1 и y k2x b2 называют наклонными асимптотами графика функции y f x , x R соответственно при x и x , если существуют пределы:
|
|
|
|
|
k |
lim |
f x |
; |
b |
lim |
f x |
k x ; |
|
||||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
1 |
x |
x |
1 |
x |
|
1 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
k |
2 |
lim |
|
f x |
; |
b |
lim |
f x k |
2 |
x . |
|
|||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
x |
x |
2 |
x |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
- |
Прямые |
y b1 |
и |
y b2 |
называют |
горизонтальными асимптотами графика |
|||||||||||||
функции |
y f x , |
|
x R |
соответственно |
при |
x |
и x , если |
||||||||||||
b |
|
lim f x , b |
|
lim |
f x . |
|
|
|
|
|
|
|
|
|
|
||||
1 |
|
x |
2 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
При выполнении п.2.1 надо воспользоваться определением и условиями мо- |
|||||||||||||||||
нотонности функции на интервале a,b . |
|
|
|
|
|
|
|||||||||||||
- Функцию f x , |
x X , называют: |
|
|
|
|
|
|
|
|||||||||||
|
|
возрастающей на a,b X , если x1,x2 a,b x1 |
x2 |
f x1 f x2 ; |
|||||||||||||||
|
|
убывающей на a,b X , если x1,x2 a,b |
x1 x2 f x1 f x2 ; |
||||||||||||||||
|
|
неубывающей на a,b X , если x1,x2 a,b |
x1 |
x2 |
f x1 f x2 ; |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
невозрастающей на a,b X , если x1,x2 a,b (x1 x2 f x1 f x2 ). (Функции перечисленных типов называют монотонными на a,b ).
- Если функция y f x , x X , дифференцируема на a,b X , то между ха- |
||
рактером монотонности функции на a,b и знаком ее производной |
f x |
на этом |
интервале имеется следующая взаимосвязь: |
|
|
f x 0 f x возрастает; |
|
|
f x 0 f x убывает; |
|
|
f x 0 f x не убывает; |
|
|
f x 0 f x не возрастает; |
|
|
f x 0 f x const. |
|
|
В простейших случаях область определения X функции y f x |
может |
|
быть разбита на определенное число интервалов монотонности критическими
точками для функции f x по первой производной, т.е. точками, в которых
f x 0 или f x не существует (точки, в которых f x 0 называют точка-
ми стационарности функции f x ).
При выполнении п.2.2 надо воспользоваться определениями, необходимыми и достаточными признаками существования внутреннего локального экстремума
(минимума, максимума) функции.
- Точку x0 открытого промежутка X называют точкой локального максимума
(минимума), а значение функции в ней – локальным максимумом (минимумом)
функций y f x , x X , если у нее существует такая окрестность, для каждой точки которой выполняется неравенство f x f x0 f x f x0 .
- Если для любой точки x (x x0) из ее окрестности имеет место строгое нера-
венство f x f x0 f x f x0 ,то точку x0 называют точкой строгого ло-
кального максимума (минимума), а значение функции в ней – строгим локальным максимумом (минимумом) функции.
16
- Точки локального максимума и локального минимума называют точками ло-
кального экстремума, а значения функции в них – локальными экстремумами
функции.
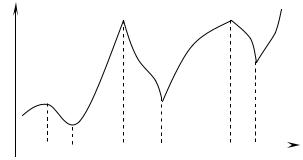
На рис.6 изображен график функции y f x , y которой x0, x2 и x4 – точки
максимума; x1, x3 и x5 – точки минимума.
Необходимое условие существования экстремума: если x0 – точка экстремума
функции f x , то f x0 0 |
или f x0 не существует (точки, критические для |
f x по первой производной, |
и только они являются точками возможного экстре- |
мума функции f x ). |
|
y |
|
|
|
|
|
x |
|
0 |
x0 x1 |
x2 |
x3 |
x4 x5 |
|
|
|
|
Рис. 6 |
|
|
Первое достаточное условие существования экстремума: точка x0 X яв- |
|||||
ляется точкой строгого локального экстремума функции f x , |
x X , если вы- |
||||
полняются следующие условия: |
|
|
|
|
|
1)f x непрерывна в x0, дифференцируема в некоторой ее окрестности за исключением, быть может, самой точки x0;
2)f x при переходе x через x0 слева направо меняет знак (при перемене знака с «–» на «+» точка x0 является точкой строгого локального минимума; при перемене знака с «+» на «–» точка x0 является точкой строгого локального мак-
симума (рис.7, 8).
Если же при выполнении условия 1 производная f x при переходе x через
x0 сохраняет знак, то x0 не является точкой экстремума (рис.9).
17

y |
f x 0 |
|
y |
|
|
y |
|
|
|
|
|
|
f x 0 |
|
|
f x 0 |
|
|
|
|
|
|
|
f x 0 |
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
f x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
x0 |
x |
0 |
x0 |
x |
0 |
x0 |
x |
|
|
Рис. 7 |
|
Рис. 8 |
|
|
Рис. 9 |
|
|
|
Второе достаточное условие существования экстремума: точка x0 X явля-
ется точкой строгого локального экстремума функции f x , x X , если
1) |
f x |
имеет в x0 производные до порядка n(n 2) включительно, причем |
|
f x0 f x0 ... f n 1 x0 0, f n x0 0; |
|||
2) |
n – четное; при этом точка x0 |
является точкой строгого локального мини- |
|
мума, |
если |
f n x 0, и точкой |
строгого локального максимума, если |
|
|
0 |
|
f n x0 0.
В частности, x0 X является точкой строгого локального минимума функции
f x , x X , если |
f x0 0, f x0 0, и точкой строгого локального максиму- |
ма, если f x0 0, |
f x0 0 (рис.10, 11). |
Если же при выполнении условия 1 этой теоремы n является нечетным, то x0 не является точкой экстремума функции.
y |
f x0 0 |
y |
f x0 0 |
||
|
f x0 0 |
|
f x0 0 |
||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
x |
x |
0 |
x0 |
x |
|
0 |
|
|
|
|
|
Рис.10 |
|
|
Рис. 11 |
|
При выполнении п.2.3 надо воспользоваться определениями и признаками выпуклости (вогнутости), строгой выпуклости (строгой вогнутости) функции на интервале a,b .
- Дифференцируемую функцию f x , x X называют выпуклой (вогнутой)
18
на a,b X , если для любых x, x0 a,b таких, что x x0, выполняется
f x f x0 f x0 x x0 f x f x0 f x0 x x0 .
- Дифференцируемую функцию f x , x X , называют строго выпуклой
(строго вогнутой) на a,b X , если для любых x, x0 a,b таких, что x x0,
выполняется
f x f x0 f x0 x x0 f x f x0 f x0 x x0 .
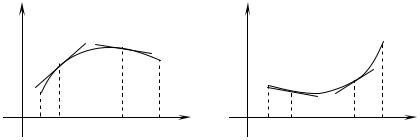
График выпуклой на a,b функции лежит не выше любой своей касательной
(рис.12).
График вогнутой на a,b функции лежит не ниже любой своей касательной
(рис.13).
y |
|
|
|
|
y |
|
|
|
|
|
|
M0 |
M1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
M1 |
|
|
|
|
|
|
|
|
|
M0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
x |
0 |
a |
x |
x |
b |
0 |
a |
x |
x |
b |
|
0 |
1 |
|
|
0 |
1 |
|
||
|
|
|
Рис. 12 |
|
|
|
Рис. 13 |
|
|
Для того чтобы дважды дифференцируемая на a,b X |
функция y f x , |
||||||||
x X , была выпуклой (вогнутой) на |
a,b , необходимо и достаточно, чтобы на |
||||||||
этом интервале |
|
|
|
|
|
|
|
|
|
|
|
|
f x 0 f x 0 . |
|
|
||||
Для того, чтобы дважды дифференцируемая на a,b X |
функция y f x , |
||||||||
x X , была строго выпуклой (строго вогнутой) на |
a,b , достаточно, чтобы на |
этом интервале |
|
f x 0 f x 0 . |
|
В простейших случаях область определения |
X функции y f x может |
быть разбита на определенное число интервалов выпуклости и вогнутости функ-
19
ции критическими точками функции f x по второй производной, т.е. точками, в
которых f x 0 или f x не существует (точки, в которых |
f x 0, назы- |
вают точками стационарности функции f x ). |
|
При выполнении п.2.4 кроме определения используют необходимые и доста-
точные признаки существования точки перегиба: |
|
|
Точку x0 X называют точкой перегиба функции |
f x , |
x X , если в ней |
функция имеет конечную либо бесконечную производную и эта точка отделяет интервал строгой выпуклости функции от интервала строгой вогнутости.
|
Если |
x0 – точка |
перегиба |
функции |
y f x , то |
в этом случае точку |
||
x0, f |
x0 |
называют точкой перегиба графика функции, |
т.е. график функции |
|||||
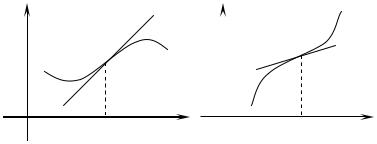
f x |
в точке x0, f x0 |
«перегибается» через касательную, проведенную к нему |
||||||
в этой точке, переходит с одной стороны касательной на другую (рис.14, 15). |
||||||||
|
|
y |
|
|
y |
|
|
|
|
|
|
|
|
|
x0, f x0 |
|
|
|
|
|
x0, f x0 |
|
|
|
|
|
|
|
0 |
x0 |
x |
0 |
x0 |
x |
|
|
|
|
Рис. 14 |
|
|
Рис. 15 |
|
|
|
Если x0 – точка перегиба функции |
f x , то f x 0 или |
f x не суще- |
|||||
ствует (точки перегиба отыскиваются среди точек, в которых |
f x 0 или |
|||||||
f x не существует, т.е. среди критических точек для функции |
f x по второй |
|||||||
производной). |
|
|
|
|
|
|
||
Точка x0 X является точкой перегиба функции f x , x X , если:
1)f x дифференцируема в x0, дважды дифференцируема в некоторой окрестности этой точки, за исключением, быть может, самой точки x0;
2)f x меняет знак при переходе x через x0.
20
