Перевод чисел из восьмеричной системы счисления в двоичную и наоборот

Существует особый случай перевода, если основание одной системы счисления является целой степенью основания другой системы. В этом случае перевод чисел существенно упрощается. В ЭВМ наиболее часто используется переход между 8-ричной и 2-ичной системами. Поэтому ограничимся рассмотрением только этого случая.

Пусть задано число А в 8-ричной системе:

A=a_n-1 a_n-2…a₁ a₀₍₈₎ = a_n-1´8^n-1+a_n-2´8^n-2+…+a₁´8¹+a₀´8⁰.

Пусть число А записано в 2-ичной системе счисления:

A=b_l-1 b_l-2…b₂ b₁ b_{0 (2)} = b_l-1´2^l-1+b_l-2´2^l-2+…+b₂´2²+b₁´2¹+b_0.

Так как числа одинаковые, мы можем приравнять их друг другу:

a_n-18^n-1+a_n-28^n-2+…+a₁8¹+a₀8⁰= b_l-1 2^l-1+2_l-2 2^l-2+…+b₂ 2²+b₁ 2¹+b₀ 2⁰ .

Если разделить обе части равенства на 8, то получим одинаковые частные

a_n-1 8^n-2 + a_n-2 8^n-3 +…+ a₁ = b_l-1 2^l-4 + b_l-2^l-5 +…+ b₄ 2¹ + b₃

и одинаковые остатки:

a₀₍₈₎=b₂2² + b₁2¹ + b₀2⁰ = b₂ b₁ b_{0 (2)}.

Следовательно, младшая восьмеричная цифра a₀₍₈₎выражается трехразрядным двоичным числом b₂b₁b₀₍₂₎.

Если частное вновь разделить на 8, то получим

а₁₍₈₎=b₅b₄b₃₍₂₎.

Аналогично можно получить все остальные разряды.

Правило перевода. Для перевода восьмеричного числа в двоичную систему счисления достаточно каждую восьмеричную цифру заменить равным ей трехразрядным двоичным числом (двоичной триадой).

Пример 3.14. Перевести восьмеричное число 571,034 ₍₈₎в двоичное.

Решение. .

Для перевода числа из двоичной системы в восьмеричную достаточно разбить его вправо и влево от запятой на триады и заменить каждую триаду соответствующей ей восьмеричной цифрой. Если крайние триады окажутся неполными, их следует дополнить нулями.

Пример 3.15. Перевести двоичное число 11011111011001 , 1001₍₂₎в восьмеричное.

Решение.

.

Простота перехода от восьмеричной системы к двоичной иногда используется для перевода чисел из десятичной системы счисления в двоичную: сначала от десятичной системы переходят к восьмеричной, а затем уже к двоичной.

Лекция 5. Способы представления в ЭВМ отрицательных чисел

В ЭВМ нашли широкое распространение три способа представления (кодирования) чисел в прямом, обратном и дополнительном кодах.

Как уже указывалось ранее, для запоминания одной двоичной цифры в ЭВМ используется элемент с двумя устойчивыми состояниями 0 и 1. Для хранения k-разрядного двоичного числа берут k таких элементов, совокупность которых называется регистром.

Пусть в ЭВМ для записи числа А отводится n разрядов под целую часть, m под дробную часть и один разряд под знак числа:

an

an-1

an-2

…

a1

a0

a-1

…

a-m

Прямой код

Прямой код соответствует обычной записи числа со своим знаком. Положительное число имеет в знаковом разряде символов 0, отрицательное – 1. Прямой код обозначают [A]_пр, а знаковый разряд отделяют от цифровых разрядов точкой.

Ч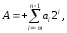исла в прямом коде представляются в форме:

при А ³ 0 [A]_пp = 0.a_n-1a_n-2 … a₁a₀,a_-1 … a_-m;

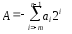(3.2 )

при А £ 0 [A]_пр = 1.a_n-1a_n-2 … a₁a₀,a_-1 … a_-m ;

Пример 3.16.

А =+11011,1001; [A]_пр=0.11011,1001 (n=5, m=4).

Пример 3.17.

В =-1010,101, [В]_пр=1.1010,101 (n=4, m=3).

Число нуль в прямом коде имеет два изображения:

+ 0 : [0]_пр= 0.00…0, - 0 : [0]_пр = 1.00…0.

Прямой код применяется при вводе и выводе информации в ЭВМ, а также при хранении чисел в запоминающем устройстве. В прямом коде просто выполняется умножение чисел. Однако при выполнении операции алгебраического сложения ЭВМ должна выполнять и сложение, и вычитание чисел. Применение обратных и дополнительных кодов позволяет операцию вычитания заменить операцией сложения.

Общая идея представления отрицательных чисел в обратном и дополнительном кодах заключается во введении специального разряда с отрицательным весовым коэффициентом. Число А записывают в форме:

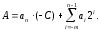
( 3.3 )

Здесь a_n– не знаковый разряд , он будет участвовать во всех операциях. Как увидим, введение этого разряда позволит заменить операцию вычитания операцией алгебраического сложения чисел с разными знаками. Для удобства разряд a_nвсе равно называют знаковым. При записи чисел разряд с отрицательным весовым коэффициентом отделяют точкой.

Обратный код

Для образования обратного кода коэффициент С в выражении (3.3) выбирается равным максимальному числу, которое может быть записано в регистре с n целыми и m дробными разрядами:

С = 2ⁿ-2^-m.

Двоичное число в обратном коде записывается в виде

[A]_обр = b_n.b_n-1 … b₁b₀,b_-1 … b_-m,

при этом число А определяется как:

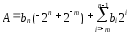
( 3.4 )

Пример 3.18. Найти значения двоичных чисел, записанных в обратном коде:

[A₁]_обр = 0.110,11, [A₂]_обр = 1.011,01 (n=3, m=2).

Решение. А₁=0^. (-2⁺³+2^-2)+110,11=+110,11.

А₂= 1^. (-2⁺³+2^-2)+011,01=-1000+0,01+011,01=-100,10.

Как видим, положительные числа в прямом и обратном кодах имеют одинаковую форму записи.

Ч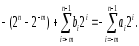тобы найти правило перехода от прямого кода отрицательного числа к обратному, приравняем правые части соотношений (3.2) и (3.4). Учитывая, что в соотношении (3.4 ) для отрицательных чисел b_n=1, получим:

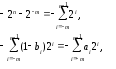
Так как то

Следовательно, b_i=1-a_i, т.е. если a_i=0, то b_i=1 и если a_i=1, то b_i=0.

Правило:Для получения обратного кода для отрицательного числа следует в разряд с отрицательным весовым коэффициентом записать 1, а в остальных разрядах прямого кода заменить 1 на 0, а 0 на 1. Аналогично образуется и прямой код отрицательного числа из обратного.

Пример 3.19. Получить обратный код для числа А = -10101,1011.

Решение. [A]_пр= 1.10101,1011, [A]_обр= 1.01010,0100.

Важно заметить, что в обратном коде отрицательного числа нули, записанные в конце числа после запятой и в начале числа, после 1, отделенные точкой, отбрасывать нельзя, но можно отбрасывать записанные на этих позициях 1.

Нуль в обратном коде имеет два представления:

+ 0 : [0]_обр= 0.00 … 0, - 0 : [0]_обр= 1.11 … 1.

Сложение чисел в обратном коде

Покажем, что при использовании обратного кода вычитание можно заменить сложением в обратном коде. При этом сумма обратных кодов равна обратному коду алгебраической суммы.

Рассмотрим возможные случаи при сложении чисел В и С : В+С=D.

1. B > C , C > 0. Так как положительные числа в прямом и обратном кодах записываются одинаково, то и складываются они по известному правилу.

2. Рассмотрим сложение чисел с разными знаками: В > 0, C < 0.

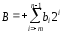
[B]_обр= 0.b_n-1b_n-2… b₁b₀,b_-1… b_-m,

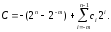
[C]_обр = 1.c_n-1c_n-2… c₁c₀,c_-1… c_-m, .

Тогда

[B]_обр+ [C]_обр= [D]_обр = d_n.d_n-1… d₁d₀,d_-1… d_-m,

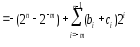
D . (3.5)

Рассмотрим два случая в выражении (3.5):

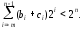
1.

Тогда нет переноса в n–й разряд и [D]_обр имеет вид:

[D]_обр= 1.d_n-1… d₁d₀,d_-1… d_-m,

т.е. результат получаем, пользуясь обычными правилами сложения.

Пример 2.20. Сложить два числа в обратных кодах: В = + 3₍₁₀₎,

С = - 5₍₁₀₎, n=3, m=0.

Решение. В = + 011₍₂₎, С = - 101₍₂₎.

[B]_обр=0.011

[C]_обр=1.010

[D]_обр=1.101 .

[D]_пр= 1.010, D = - 010₍₂₎= - 2₍₁₀₎, т.е. + 3₍₁₀₎+ (-5)₍₁₀₎= - 2₍₁₀₎.

2.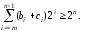

В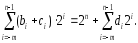данном случае имеется единица переноса в n-ный разряд и тогда можно записать:

Подставив это выражение, получим:

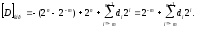
Отсюда следует , что для получения обратного кода суммы необходимо к результату сложения чисел прибавить единицу младшего разряда.

Заметим, что в этом случае при сложении чисел по обычным правилам появится 1 переноса из разряда с отрицательным весом, которая также участвует в операции сложения.Это и является формальным признаком того, что необходимо добавить 1 в младший разряд. Такая операция называетсяциклическим переносом.

Пример 3.21. Сложить два числа в обратных кодах: В = +5 ₍₁₀₎,

С = -3 ₍₁₀₎, n = 3, m = 0.

Решение. В = +101₍₂₎, С = - 011₍₂₎.

[B]_обр= 0.101

[C]_обр= 1.100

0.001

+1

[D]_обр= 0.010

[D]_пр= 0.010, D = + 010₍₂₎= + 2₍₁₀₎, т.е. +5₍₁₀₎+ (-3)₁₀= +2₍₁₀₎.

3. В < 0, C < 0. В этом случае аналогично можно показать , что и при сложении двух отрицательных чисел необходимо выполнять циклический перенос.

Пример 3.22. Сложить два числа в обратных кодах: В = - 2₍₁₀₎, С = - 5₍₁₀₎, n=3, m=0.

Решение. В = - 010₍₂₎, С = -101₍₂₎.

[B]_обр= 1.101

[C]_обр= 1.010

0.111

+1

[D]_обр= 1. 000

[D]_пр= 1.111, D = - 111₍₂₎= - 7₍₁₀₎, т.е. (-2)₁₀+ (-5)₁₀= -7₁₀.

Правило сложения в обратных кодах.Сложение чисел в обратных кодах выполняется по обычным правилам, причем знаковый разряд участвует в операции сложения наравне с обычными разрядами. При появлении единицы переноса из знакового разряда (или разряда с отрицательным весом) ее следует циклически перенести в младший разряд и просуммировать с полученным ранее результатом.

Заметим, что это правило чисто формально приводит к правильному результату, а фактически выполнять сложение единиц с разными весами нельзя. Просто при наличии переноса для получения обратного кода необходимо добавить единицу в младший разряд. Для этого и используется единица переноса.

Дополнительный код

Идея образования дополнительного кода возникла в связи со стремлением избавиться от операции циклического переноса, которая приводит к увеличению времени выполнения операции сложения. Оказывается , что для устранения циклического переноса достаточно уменьшить величину отрицательного веса С на единицу младшего разряда: С = 2_n. Тогда двоичное число в дополнительном коде имеет вид:

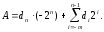[A]_доп = d_n . d_n-1 … d₁ d₀, d_-1…d_-m,

Правило. Положительные числа в прямом и дополнительном кодах имеют одинаковую форму записи. Для записи отрицательного числа в дополнительном коде достаточно образовать обратный код этого числа и к нему прибавить единицу младшего разряда 2^-m.

Пример 3.23. Получить дополнительный код для чисел: A=+1001,101₍₂₎, B=-1000,010₍₂₎(n=4, m=3).

Решение: [A]_доп.=0.1001,101. [B]_обр.=1.0111,101

1

[B]_доп.=1.0111,110

Для образования прямого кода отрицательного числа из дополнительного кода следует вычесть единицу младшего разряда (получим обратный код) и заменить 1 на 0, а 0 на 1 (получим прямой код).

Рассмотренный метод неудобен тем, что содержит операцию вычитания. В ЭВМ прямой код отрицательного числа получают путем образования дополнительного кода от дополнительного, т.е. образуется обратный код и к нему прибавляется 1 младшего разряда.

Пример 3.24. Получить прямой код из дополнительного: [B]_доп.=1.0111,110.

Решение. ([B]_доп.)_обр.=1.1000,001

1

[B]_пр.=1.1000,010

Как представляется нуль в дополнительном коде:

+0: [0]_доп.= 0.000…00 ,

-0: [0]_доп.=1.111 … 1

+ 1

[0]_доп.=0.000 … 0 ,

т.е. нуль в дополнительном коде имеет единственное представление.

Правило сложения в дополнительных кодах. Для того чтобы при сложении дополнительных кодов двух чисел получить дополнительный код суммы, необходимо сложить дополнительные коды слагаемых по правилам сложения двоичных чисел, рассматривая знаковые разряды как обычные цифровые. При возникновении единицы переноса из знакового разряда ее следует опустить.

Пример 3.25. Сложить в дополнительных кодах числа:

А₁=+7₍₁₀₎= +111₍₂₎и В₁=-3₍₁₀₎= -011₍₂₎,

А₂=-7₍₁₀₎= -111₍₂₎и В₂=+3₍₁₀₎= +011₍₂₎.

Решение.

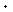
[A₁]_доп = 0.111 [A₂] _доп = 1.001

[B₁]_доп = 1.101 [B₂] _доп = 0.011

[C₁]_доп= 0.100, [C₂] _доп= 1.100

[C₂]_пр= 1.100

С₁= + 100₍₂₎= + 4₍₁₀₎, С₂= -100₍₂₎= - 4₍₁₀₎.

Сравнивая представление чисел в различных кодах, можно сделать следующие выводы:

- перевод чисел из прямого кода в обратный осуществляется проще, чем в дополнительный;

- в дополнительном коде проще выполняется сложение, т.к. отсутствует циклический перенос.

Поэтому обратный и дополнительный коды примерно равноценны при их реализации на ЭВМ.

Лекция 6. Переполнение разрядной сетки

В ЭВМ количество разрядов, используемых для представления чисел, ограничено. Поэтому при сложении двух чисел с одинаковыми знаками их сумма может оказаться больше по модулю, чем максимальное число, которое может быть записано при заданном количестве разрядов и результат сложения окажется неверным. Такое явление называется переполнением разрядной сетки.

Пример 3.26. Сложить два числа А = + 1101,1 и В = + 1011,0 (n=4, m=1) в обратном коде.

Р

+

ешение. [A]_обр= 0.1101,1

[B] _обр= 0.1011,0

[C] _обр= 1.1000,1

В этом примере 1 переноса из старшего разряда попадает в знаковый разряд ( с отрицательным весом) и , следовательно, в результате сложения двух положительных чисел получается отрицательное число.

При сложении отрицательных чисел в обратном или дополнительном кодах переполнение разрядной сетки наступает в том случае, если отсутствует 1 переноса в разряд с отрицательным весом и результат оказывается положительным.

Пример 3.27. Сложить два числа А = - 1011 и В= - 1101 (n=4, m=0) в дополнительном коде .

Р

+

ешение: [A]_доп= 1.0101

[B]_доп= 1.0011

[C]_доп= 0.1000

Для обнаружения переполнения разрядной сетки используют следующие способы:

1. Сравнивают знаки слагаемых со знаком суммы. Сигнал переполнения вырабатывается тогда, когда знаки слагаемых одинаковы и не совпадают со знаком суммы.

2. Второй способ основан на применении модифицированных кодов. Модификация кодов заключается во введении дополнительного разряда, который располагается перед знаковым. Этот разряд часто называют разрядом переполнения. Иногда говорят, что модифицированные коды содержат два знаковых разряда. Положительные числа имеют в знаковых разрядах два нуля, отрицательные – две единицы. При использовании модифицированных обратного и дополнительного кодов признаком переполнения разрядной сетки является наличие в знаковых разрядах различных цифр 01 или 10.

Пример 3.28. Сложить числа А₁= +1011 и В₁= +1101, А₂= -1100 и В₂= -1101 (n=4, m=0) соответственно в модифицированных дополнительном и обратном кодах.

Р

+1

ешение.

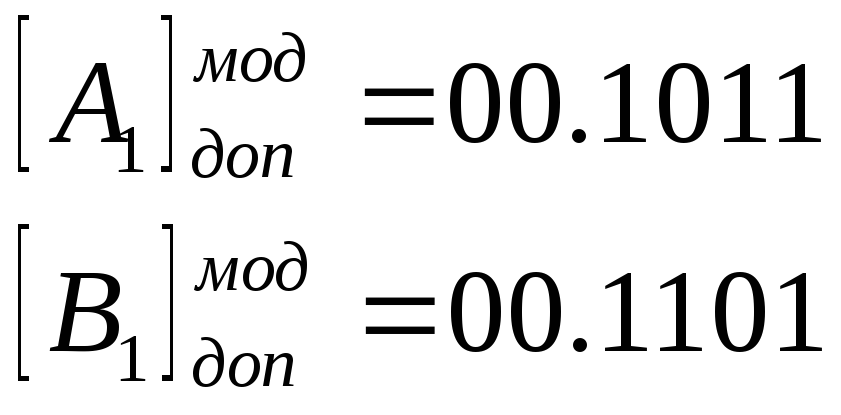
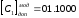
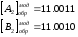
В обоих примерах произошло переполнение разрядной сетки.

При несовпадении знаковых разрядов в модифицированных кодах вырабатывается сигнал переполнения разрядной сетки.

Формы представления в ЭВМ числовых данных

В математике широко используются две формы записи чисел: естественная и нормальная.

При естественной формечисло записывается в естественном натуральном виде, например: 28759 – целое число, 0,01372 – правильная дробь, 25,0265 – неправильная дробь.

При нормальной формезапись одного и того же числа может быть различной в зависимости от ограничений, накладываемых на ее форму. Например, число 28759 может быть записано так:

28759=2,8759 ^.10⁴=287590^. 10^-1=0,28759^. 10⁵и т.д.

При естественном представлении чисел в ЭВМ устанавливается длина разрядной сетки, а также число разрядов, отводимых под целую и дробную части числа. При этом распределение разрядов между целой и дробной частями не изменяется и остается постоянным независимо от величины числа, т.е. положение запятой в разрядной сетке ЭВМ строго фиксировано. Поэтому существует также и другое название этой формы представления чисел – с фиксированной запятой.

Например, если под целые части отведено 3 разряда (n=3), а под дробную часть – 4 разряда (m=4), то числа запишутся в виде:

000,0000

000,0001

000,0010

.………..

111,1110

111,1111.

Здесь число 000,0001 наименьшее (отличное от нуля) двоичное число, а 111,1111 – наибольшее число, представленное при данной разрядной сетке. Всякое число, большее нуля, но меньшее 0,0001, будет представлено нулем (это так называемый машинный нуль). Числа, большие 111,1111 в данной разрядной сеткене могут быть представлены, т.к. при записи таких чисел часть старших разрядов теряется.

Возникает вопрос, в каком месте разрядной сетки ЭВМ целесообразнее фиксировать запятую? Как правило запятую фиксируют или перед старшим цифровым разрядом чисел (машина оперирует с числами, меньшими единицы, т.е. n=0), или в конце разрядной сетки (машина оперирует с целыми числами, т.е. m=0).

При машинном представлении чисел один разряд отводится под знак числа, а остальные образуютполе числа(рис.3.1). Знаковый разряд может располагаться как в начале, так и в конце числа. Обычно знак положительного числа изображается символом0, а знак отрицательного числа - символом 1.

а) номер разряда

0

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

знак поле числа

б)

1

1

0

1

0

1

1

1

0

0

1

0

1

0

0

1

,- 0,101011100101001

в)

0

0

0

1

0

0

0

1

1

1

1

1

0

1

1

1

+ 001000111110111 ,

Рис.3.1

На рис.3.1 приведены примеры записи чисел в форме с фиксированной запятой отрицательного числа (запятая фиксирована перед старшим разрядом, n=0) и положительного целого числа (запятая фиксирована в конце разрядной сетки,m=0).

Если поле числа включает в себя mразрядов и запятая фиксирована перед старшим разрядом, то диапазон представления чисел в этом случае ограничивается значениями –(1-2^-m)¸+ (1-2^-m).

Представление чисел в ЭВМ в нормальной форме называют так же представлением с плавающей запятой, т.к. положение запятой в записи числа, как показывают приведенные выше примеры, в этом случае может изменяться.

В нормальной форме записи число А представляется в виде

A=M ^. q^П,

где М – мантисса числа, определяющая значащие цифры числа, q – основание системы счисления, П – порядок числа, определяющий положение запятой в числе.

Формат машинного изображения числа с плавающей запятой содержит поля для мантиссы (m разрядов) и порядка (р разрядов) и по одному разряду для знака мантиссы и знака порядка (рис.3.2., m=9, p=5). Очевидно, что знак мантиссы является и знаком числа. Кодирование знаков остается таким же, как и при представлении чисел в форме с фиксированной запятой.

Обычно в ЭВМ запятая в мантиссе фиксируется перед старшим знаковым разрядом, а порядок представляет собой целое число. Чтобы избежать неоднозначности представления чисел используют так называемую нормализованную форму, для которой справедливо следующее условие:

q^-1 £½m½< 1. (3.6)

Так десятичные числа 42,56 ^. 10²и 0,00374^. 10^-4в нормализованном виде должны быть записаны следующим образом: 0,4256^. 10⁴и 0,374^. 10^-6. Для двоичной системы счисления нормализованные числа в старшем разряде мантиссы имеют 1.

Рассмотрим примеры записи чисел в форме с плавающей запятой. Пусть в разрядную сетку ЭВМ (рис.3.2) необходимо записать двоичные числа А₁=-10110,1111 и А₂=+0,000110000111. Прежде всего эти числа необходимо нормализовать. Порядок чисел выбираем таким образом, чтобы для них выполнялось условие (3.6), т.е. А₁=-0,101101111^. 2⁵и А₂=+0.110000111^. 2^-3. Порядок должен быть записан также в двоичной системе.

а)

0

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

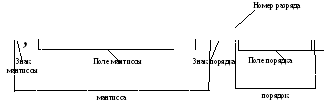
б)

1

1

0

1

1

0

1

1

1

1

0

0

0

1

0

1

А₁= - 0,101101111^. 2⁺⁵

в)

0

1

1

0

0

0

0

1

1

1

1

0

0

0

1

1

А₂= + 0,110000111^. 2^-3

Рис.3.2

Для изображения порядка выделено пять цифровых разрядов и один знаковый разряд, поэтому машинные изображения порядков запишутся как П_А1=000101 и П_А2=100011. При этом машинные изображения мантисс будут равны соответственно: М_А1=1101101111 и М_А2=0110000111.

Изображения чисел А₁и А₂в форме с плавающей запятой показаны на рис.3.2б и 3.2в.

Представление числовой информации в ЭВМ, как правило, влечет за собой появление погрешностей (ошибок), значения которых зависят как от формы представления чисел, так и от длины разрядной сетки ЭВМ.

Абсолютная погрешностьпредставления – это разность между числом А и его значением, полученным из машинного изображения А_М:

D[A] = A - A_M.

Относительная погрешностьпредставления – это отношение абсолютной погрешности представления числа к его значению в машинном представлении:

d[A] =D[A] / A_M.

Целые числа представляются в машине без погрешностей. Максимальная абсолютная погрешность представления правильной дроби в форме в фиксированной запятой равна половине значения младшего разряда разрядной сетки, т.е.

D[A]_{max ф.з.}= 2^-m / 2 = 2^-m-1,

где m - длина разрядной сетки для представления дробной части числа. Тогда минимальная и максимальная относительные погрешности представления правильной дроби в форме с фиксированной запятой определятся соответственно следующим образом:

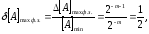
Таким образом имеем неодинаковую относительную погрешность чисел в форме с фиксированной запятой, причем погрешности представления малых чисел могут быть значительными.

При представлении чисел в форме с плавающей запятой максимальная абсолютная погрешность определяется половиной значения младшего разряда мантиссы и кроме того она зависит от величины порядка:

Отсюда относительная ошибка определится как

которая достигает максимума при минимальной нормализованной мантиссе

и минимума при максимальной мантиссе

Из этого следует, что относительная погрешность представления чисел в форме с плавающей запятой практически не зависит от величины числа и примерно постоянна во всем диапазоне представления чисел.