4. Раздел 2

5. Логические основы информатики Лекция 2. Основные понятия и определения

В ЭВМ обрабатывается числовая информация, представленная в двоичной системе счисления (0 и 1). Любую схему ЭВМ можно рассматривать как устройство, имеющее n входных сигналов и m выходных. Поступления на входы некоторойпоследовательности 0 и 1 вызывает появление на выходах вполне определеннойпоследовательности 0 и 1.

В ЭВМ различают два больших класса схем: класс комбинационных (логических) схем и класс конечных автоматов. В комбинационных схемах значение выходных сигналов в момент времени t однозначно определяется входными сигналами в тот же момент времени. В конечных автоматах выходные сигналы определяются не только входными сигналами, но и состоянием схемы (конечные автоматы содержат элементы памяти).

Построение схем ЭВМ решается с помощью аппарата математической логики. При этом используется только самая простая ее часть – алгебра логики. Основным понятием в той части алгебры логики, на которой основывается ее применение к построению схем ЭВМ, является понятиепереключательной функции.

Переключательной или булевой функцией называется функция f(x_1, ,x₂, … x_n), способная принимать как и ее аргументы x₁, … , x_n только два значения 0 или 1. Любая переключательная функция (ПФ) может быть задана таблицей ее значений в зависимости от значений ее аргументов. Такая таблица называетсятаблицей истинности.

Пример. Зададим ПФ трех аргументов f(x₁, x₂, x₃). Так как каждый из аргументов принимает лишь 2 значения, поэтому мы имеем 8 различных комбинаций 3 переменных. Эти комбинации называют набором. Наборы обычно пишут в так называемом естественном порядке, когда наборы принимают значения (000), (001), … Для получения следующего набора прибавляют 1 к правому разряду – применяется как бы сложение чисел. Наборам присваивается номер, равный двоичному числу, соответствующему данному набору. Сопоставляя каждому набору одно из двух значений ПФ, мы и получим таблицу истинности (например, представленную в табл.2.1).

Таблица 2.1

Л

x1	x2	x3	f(x1,x2,x3)
0	0	0	0
0	0	1	1
0	1	0	1
0	1	1	1
1	0	0	1
1	0	1	0
1	1	0	0
1	1	1	1

юбая ПФ n аргументов определена на 2ⁿнаборах. Число различных ПФ n аргументов равно приn= 1, число различных ПФ равно 4, приn= 2 – 16, приn= 3 – 256, приn=4 – 65536, приn=5 – примерно 4,310⁹. Ясно, что прямое изучение ПФ с помощью таблиц истинности возможно для небольшого числа аргументов.

Возьмем какую либо комбинационную схему (КС) (рис.2.1).

х₁.

х₂

_.

.

.

х_n

.

.

.

Рис.2.1. Комбинационная схема

Если значения ПФ отождествить с выходным сигналом КС, а аргументов - с входными сигналами, то ПФ будет описывать процесс преобразования входных сигналов в выходные, т.е.

y₁ = f₁(x₁,x₂,…,x_n);

y₂ = f₂ (x₁,x₂,…,x_n);

.

y_m= f_m(x₁,x₂,…,x_n).

Любые сложные схемы ЭВМ строятся из простых схем, которые называют логическими элементами^.

Логическим элементом называется электронная схема, реализующая элементарную ПФ, имеющая количество входов, равное числу аргументов ПФ и только один выход.

При составлении сложных схем используют два приема: последовательное соединение элементов и перестановку входов элементов. Последовательное соединение логических элементов показано на рис.2.2.

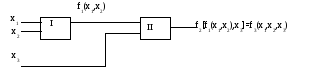
Рис.2.2. Последовательное соединение элементов

Последовательное соединение двух логических элементов позволяет получить функцию f₃трех аргументов. Подстановка в функцию вместо ее аргументов других функций называетсясуперпозицией.

Перестановка входов элементов показана на рис.2.3.

В общем случае функция f₄(x₁,x₂,x₃) отличается от функции f₃(x₁,x₂,x₃). Замена одних аргументов функции другими или изменение порядка записи аргументов называетсяподстановкойаргументов.

Рис.2.3. Перестановка входов элементов

В алгебре логики доказывается, что из ПФ одного и двух аргументов с помощью операций суперпозиции и подстановки можно получить все ПФ от большого числа аргументов. Практически это означает, что из логических элементов с одним и двумя входами можно построить любую сколь угодно сложную комбинационную схему.

Переключательные функции одного и двух переменных

Рассмотрим некоторые ПФ одного и двух аргументов. В табл. 2.2 представлены все 4 функции одного аргумента.

Таблица 2.2

x	f0(x)	f1(x)	f2(x)	f3(x)
0	0	0	1	1
1	0	1	0	1

Ф

ункция f₀ (x) равно нулю (константа нуля), f₃(x) равна единице (константа единицы), функция f₁(x) повторяет значение аргумента, т.е. f₁(x)=x. Наиболее интересной и имеющей важное значение является функция f₂(x), которая принимает значения, обратные значению аргумента-логическое отрицаниеили функция НЕ и обозначается как:

 х (читается не х).

Все ПФ двух аргументов приведены в табл.2.3.

Таблица 2.3

х1	х2	f0	f1	f2	f3	f4	f5	f6	f7	f8	f9	f10	f11	f12	f13	f14	f15
0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
0	1	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
1	0	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
1	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1

Функции f₀(x₁,x₂) и f₁₅(x₁,x₂) не зависят от значений аргументов: f₀(x₁,x₂)=0 и f₁₅(x₁,x₂)=1. Функции f₃(x₁,x₂), f₅(x_1, x₂), f₁₀(x₁,x₂) и f₁₂(x₁,x₂) являются фактически функциями одного аргумента:

f₃(x₁,x₂)=x₁, f₅(x₁,x₂)=x₂, f₁₀(x₁,x₂)=x₂и f₁₂(x₁,x₂)=x₁.

Рассмотрим часто встречающиеся ПФ. Функция f₁(x₁,x₂) реализует операциюконъюнкцииилилогического произведения. Как видим из табл.2.3 , функция f₁(x₁,x₂) равна 1, когда и x₁и x₂равны 1. Конъюнкция обозначается как

f₁(x₁,x₂)=x₁x₂ = x₁x₂ = x₁x₂ (читается x₁и x₂).

Функция f₇(x₁,x₂) реализует операциюдизъюнкциюилилогического сложения. Функция равна 1, когда или x₁или x₂равны 1. Дизъюнкция обозначается как

f₇(x₁,x₂)=x₁x₂.

Функция f₁₄(x₁,x₂) реализует операциюотрицания конъюнкции. Из табл.2.3 видно, что когда конъюнкция f₁(x₁,x₁) равна 0, то функция f₁₄(x₁,x₂) равна 1, а если f₁(x_1, x₂) равна1, то f₁₄(x₁,x₂) равна 0, т.е. f₁₄(x₁,x₂)=f₁(x₁,x₂). Эта операция получила название “штрих Шеффера” и обозначается различными способами:

Функция f₈(x₁, x₂) реализует операциюотрицания дизъюнкции. По аналогии с функцией отрицания конъюнкции, из табл.2.3 видно, что f₈(x₁, x₂)=f₇(x₁, x₂). Эта операция также получила отдельное название – “стрелка Пирса” и обозначается следующим образом:

Функция f₆(x₁, x₂) реализует операциюлогической неравнозначностиили еще ее называют суммой по модулю два. ПФ равна 1, если аргументы x₁и x₂не равны между собой.

Остальные ПФ двух аргументов рассматривать не будем. Вдействительности, для реализации сколь угодно сложной ПФ не обязательно использовать все 16 ПФ двух аргументов. Можно ограничиться некоторым набором, с помощью которого можно строить любые ПФ.

Система ПФ, из которых с помощью операций суперпозиции и подстановки можно получить любую сколь угодно сложную ПФ, называется функционально полной системой переключательных функций (ФПС ПФ). Существует несколько ФПС ПФ:

- дизъюнкция, конъюнкция и отрицание;

- отрицание конъюнкции;

- отрицание дизъюнкции и другие.

Возникает вопрос, какие ФПС ПФ представляют наибольший практический интерес? Выбор ФПС ПФ с технической точки зрения эквивалентен выбору типов логических элементов, из которых может быть построена любая логическая схема. Оказывается, что наиболее удобной для решения задач синтеза схемы является ФПС ПФ, содержащая дизъюнкцию, конъюнкцию и отрицание.