§9. Линейные образы в пространстве
Предположим, что в пространстве выбрана декартова прямоугольная система координат. Рассмотрим геометрические объекты в пространстве, определяемые линейными уравнениями.
ВЕКТОРНОЕ УРАВНЕНИЕ ПЛОСКОСТИ
Пусть в пространстве
заданы точка
и вектор
.
Следует записать уравнение плоскости,
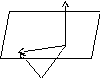
проходящей через точку
перпендикулярно вектору
(рис. 37). Точка
принадлежит плоскости тогда и только
тогда, когда
|
Рис. 37. |
Рис. 38. |
Если
и
- радиус-векторы соответственно точек
и
,
то
и равенство
примет вид
Полученному
уравнению удовлетворяют только
радиус-векторы
точек рассматриваемой плоскости,
следовательно, это – векторное уравнение
данной плоскости. Вектор
называется
нормальным вектором плоскости.
Замечание. Если
начало нормального вектора
поместить
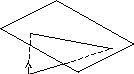
в начало координат и при этом вектор
будет направлен в сторону плоскости
(рис. 38), то произведение
,
где
- расстояние от начала координат до
плоскости. Векторное
уравнение плоскости
в
этом случае имеет вид
.
Уравнение
называется нормированным (нормальным)
уравнением плоскости.
ОБЩЕЕ УРАВНЕНИЕ ПЛОСКОСТИ
Пусть в заданной
системе координат имеем
,
тогда
и векторное уравнение плоскости в
координатной форме будет иметь вид:
.
Это уравнение
называется уравнением плоскости,
проходящей через данную точку
перпендикулярно вектору
Если ввести
обозначение
,
то получим общее уравнение плоскости
НОРМИРОВАННОЕ УРАВНЕНИЕ ПЛОСКОСТИ
Векторное
нормированное уравнение плоскости
в координатной форме имеет вид
где
- направляющие косинусы вектора
Общее уравнение
плоскости
приводится
к нормальной форме умножением обеих
частей уравнения на
,
где знак берется противоположный знаку
:
.
Замечания. 1. Чтобы записать уравнение плоскости, достаточно знать какую-либо точку этой плоскости и направление, перпендикулярное этой плоскости. Направление задается при помощи вектора.
2. Любая плоскость является алгебраической поверхностью первого порядка, так как в декартовой системе координат уравнением плоскости является алгебраическое уравнение первого порядка.
Справедливо также и обратное утверждение: поверхность первого порядка – плоскость.
Доказательство аналогично доказательству для прямой/
КОНТРОЛЬНЫЕ ВОПРОСЫ
Выведите векторное уравнение плоскости.
Запишите уравнение плоскости, проходящей через данную точку перпендикулярно данному направлению.
Выведите уравнение плоскости в нормальной форме.
§10. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ДВУХ ПЛОСКОСТЕЙ
Дано:
и
.
УГОЛ МЕЖДУ ПЛОСКОСТЯМИ
Угол
между плоскостями
и
равен углу между их нормальными векторами
и
:
/
УСЛОВИЕ ПЕРПЕНДИКУЛЯРНОСТИ ДВУХ ПЛОСКОСТЕЙ
или
УСЛОВИЕ ПАРАЛЛЕЛЬНОСТИ ДВУХ ПЛОСКОСТЕЙ
или
КОНТРОЛЬНЫЕ ВОПРОСЫ
Напишите формулу для вычисления угла между плоскостями.
Напишите условия параллельности и перпендикулярности двух плоскостей.
§11. РАССТОЯНИЕ ОТ ТОЧКИ ДО ПЛОСКОСТИ
Пусть заданы
плоскость
и точка
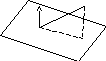
Рис. 39.
от точки
до плоскости. Задача решается аналогично
задаче в плоскости при вычислении
расстояния от точки до прямой. Искомое
расстояние где точка
принадлежит плоскости
,
вектор
- нормальный вектор этой плоскости (рис.
39). В результате вычисления
получим
Замечание. Если
уравнение плоскости задано в нормальной
форме, то
§12. ПРЯМАЯ ЛИНИЯ В ПРОСТРАНСТВЕ
ОБЩИЕ УРАВНЕНИЯ ПРЯМОЙ
Общими уравнениями прямой называется система двух уравнений
задающих эту прямую, как линию пересечения двух плоскостей.c
ВЕКТОРНОЕ УРАВНЕНИЕ ПРЯМОЙ
0
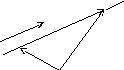
Рис. 40
и вектор
.
Требуется определить уравнение прямой,
проходящей через точку
параллельно вектору
(рис. 40). Точка
принадлежит искомой прямой тогда и
только тогда, когда
или
Это уравнение рассматриваемой прямой,
где
- параметр,
- направляющий вектор прямой.
ПАРАМЕТРИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ
Если в заданной
системе координат
то
и из векторного уравнения прямой следует
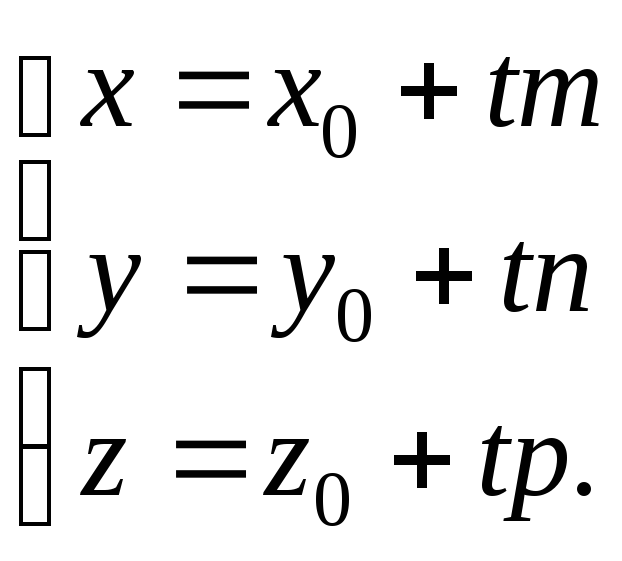
Это параметрические
уравнения прямой, где
КАНОНИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ
Записывая в
координатной форме условие
или исключая параметр
из параметрических уравнений, получим
канонические уравнения прямой:
Замечание. Направляющим вектором прямой может быть любой вектор, параллельный этой прямой.