
- •Конспект лекций
- •1.1.2.Закон кулона
- •1.1.3.Электрическое поле. Напряженность электростатического поля
- •1.1.4.Принцип суперпозиции электрических полей
- •1.1.5. Примеры расчета полей на основе принципа суперпозиции. Электрическое поле диполя
- •1.1.6. Густота линий напряженности. Поток вектора напряженности
- •1.1.7. Теорема гаусса в интегральной форме и ее применение к расчету электрических полей
- •1.1.8. Теорема гаусса в дифференциальной форме. Дивергенция векторного поля
- •1.1.9.Потенциальный характер электростатического поля. Работа сил поля при перемещении зарядов. Циркуляция и ротор векторного поля. Теорема стокса в интегральной и дифференциальной форме
- •1.1.10.Потенциал электростатического поля. Потенциальная энергия заряда в электростатическом поле
- •1.1.11. Связь между напряженностью и потенциалом
- •1.1.12. Уравнение пуассона и лапласа для потенциала
- •1.1.13. Эквипотенциальные поверхности
- •Лекция 2
- •1.2. Диэлектрики в электрическом поле
- •1.2.1.Полярные и неполярные молекулы
- •1.2.2. Диполь во внешнем электрическом поле
- •1.2.3 Поляризация диэлектриков. Ориентационный и деформационный механизмы поляризации. Дипольный момент системы зарядов. Диэлектрическая восприимчивость для полярных и неполярных диэлектриков
- •1.2.5. Вектор электрического смещения (электростатической индукции). Диэлектрическая проницаемость диэлектриков
- •1.2.6. Граничные условия для векторов напряженности электрического поля и электрического смещения
- •1.2.7. Примеры расчета электрических полей в диэлектриках
- •1.2.8. Силы, действующие на заряд в диэлектрике
- •1.3.Проводники в электрическом поле
- •1.3.1. Равновесие зарядов на приводнике. Основная задача электростатики проводников. Эквипотенциальные поверхности и силовые линии электростатического поля между проводниками
- •1.3.2.Проводник во внешнем электрическом поле. Электростатическая защита
- •1.3.3.Электроемкость проводников
- •1.3.4. Электроемкость конденсаторов
- •1.3.5. Соединения конденсаторов
- •1.4.Энергия электрического поля
- •1.4.1.Энергия взаимодействия электрических зарядов. Теорема ирншоу
- •1.4.2. Энергия заряженного проводника
- •1.4.3. Энергия заряженного конденсатора. Объемная плотность энергии электростатического поля
- •1.4.4.Энергия поляризованного диэлектрика. Объемная плотность энергии электрического поля в диэлектрике
- •1.4.5. Энергия системы заряженных проводников
- •1.4.6. Закон сохранения энергии для электрического поля в несегнетоэлектрической среде
1.1.8. Теорема гаусса в дифференциальной форме. Дивергенция векторного поля
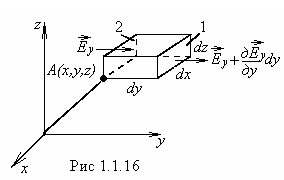 Рассмотрим теперь
дифференциальную форму теоремы Гаусса.
Пусть в некоторой точке
Рассмотрим теперь
дифференциальную форму теоремы Гаусса.
Пусть в некоторой точке
![]() с координатами
с координатами![]() напряженность поля (рис.1.1.16) равна
напряженность поля (рис.1.1.16) равна
![]() .
Построим около точки
.
Построим около точки
![]() прямоугольный бесконечно малый
параллелепипед объемом
прямоугольный бесконечно малый
параллелепипед объемом![]() .
Объемная плотность заряда в нем равна
.
Объемная плотность заряда в нем равна![]() и зависит от координат выбранной точки
поля:
и зависит от координат выбранной точки
поля:![]() .
.
Поток
вектора
![]() через правую грань (1) равен:
через правую грань (1) равен:![]() ,
,
а через левую
(2):![]() ,
,
Поэтому
поток вдоль оси
![]() равен
равен
![]()
Таким же образом
для верхней и нижней грани получим:![]() ,
,
для задней и
передней:![]() .
.
По
теореме Гаусса
![]() ,
причем
,
причем![]() - заряд, заключенный внутри объема
- заряд, заключенный внутри объема![]() (ввиду малости
(ввиду малости![]() можно считать что
можно считать что![]() внутри параллелепипеда всюду одинакова),
внутри параллелепипеда всюду одинакова),![]() ,
тогда
,
тогда
![]() ,
или
,
или
![]()
Сумма,
стоящая в левой части, называется
дивергенцией вектора
![]() ,
,
![]() ,
или
,
или
![]()
-дивергенция
вектора напряженности равна объемной
плотности зарядов, создающих поле,
деленной на
![]() .Это
выражение представляет собой теорему
Гаусса в дифференциальной форме. Она
характеризует поле в точке. Электрические
заряды являются источниками и стоками
поля вектора
.Это
выражение представляет собой теорему
Гаусса в дифференциальной форме. Она
характеризует поле в точке. Электрические
заряды являются источниками и стоками
поля вектора
![]() .
Линии вектора
.
Линии вектора![]() начинаются и заканчиваются на электрических
зарядах. Если
начинаются и заканчиваются на электрических
зарядах. Если![]() - это источник поля
- это источник поля![]() ,
если
,
если![]() - сток поля. Если
- сток поля. Если![]() ,
то в данной точке нет зарядов, линии
,
то в данной точке нет зарядов, линии![]() не прерываются.
не прерываются.
1.1.9.Потенциальный характер электростатического поля. Работа сил поля при перемещении зарядов. Циркуляция и ротор векторного поля. Теорема стокса в интегральной и дифференциальной форме
Работа,
совершаемая силами электростатического
поля при перемещении заряда
![]() на отрезок
на отрезок![]() ,
определяется выражением:
,
определяется выражением:
![]()
Разделив
на величину заряда
![]() ,
получим работу по перемещению единичного
положительного заряда:
,
получим работу по перемещению единичного
положительного заряда:![]()
Работа,
совершаемая при перемещении единичного
положительного заряда по конечному
пути
![]() ,
равна интегралу
,
равна интегралу
![]() .
(1.1.2)
.
(1.1.2)
Здесь
![]() - сила Кулона, которая является центральной
силой. Из механики известно, что поле
центральных сил консервативно.
Следовательно, работа электростатического
поля по перемещению заряда не зависит
от траектории, а определяется только
начальной и конечными ее точками. Работа
по замкнутому пути равна нулю. Поле,
обладающее такими свойствами, называется
потенциальным. Тогда из (1.1.2) имеем:
- сила Кулона, которая является центральной
силой. Из механики известно, что поле
центральных сил консервативно.
Следовательно, работа электростатического
поля по перемещению заряда не зависит
от траектории, а определяется только
начальной и конечными ее точками. Работа
по замкнутому пути равна нулю. Поле,
обладающее такими свойствами, называется
потенциальным. Тогда из (1.1.2) имеем:

![]() (1.1.3)
(1.1.3)
-
циркуляция
вектора
![]() по замкнутому пути равна нулю.Поле,
обладающее такими свойствами, называется
потенциальным.
по замкнутому пути равна нулю.Поле,
обладающее такими свойствами, называется
потенциальным.
Докажем потенциальный характер электростатического поля.
Рассмотрим
сначала работу электрических сил в поле
элементарного точечного заряда
![]() .
Работа этих сил при бесконечно малом
перемещении
.
Работа этих сил при бесконечно малом
перемещении![]() пробного единичного положительного
заряда равна:
пробного единичного положительного
заряда равна:
![]()
 ,
,
Из
рис. 1.1.17 видно, что
![]() - это
приращение численного значения
радиус-вектора
- это
приращение численного значения
радиус-вектора
![]() ,
то есть увеличение расстояния пробного
заряда
,
то есть увеличение расстояния пробного
заряда![]() от заряда
от заряда![]() .
Поэтому работа
.
Поэтому работа![]() может быть представлена как полный
дифференциал скалярной функции точки
может быть представлена как полный
дифференциал скалярной функции точки![]() :
:
 ,
,
где
![]() - численное значение радиус-вектора
- численное значение радиус-вектора![]() .
Тогда работа по перемещению единичного
положительного заряда из точки
.
Тогда работа по перемещению единичного
положительного заряда из точки![]() в точку
в точку![]() по конечному пути
по конечному пути![]() равна:
равна:
![]() ,
,
где
![]() и
и![]() - расстояния начальной и конечной точек
пути от заряда
- расстояния начальной и конечной точек
пути от заряда![]() .
Таким образом, работа электрических
сил на произвольном пути в поле
неподвижногоэлементарного
точечного заряда действительно зависит
от положений начальной и конечной точек
этого пути и не зависит от формы пути.
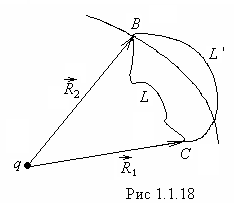
На рис.1.1.18
работа на пути
.
Таким образом, работа электрических
сил на произвольном пути в поле
неподвижногоэлементарного
точечного заряда действительно зависит
от положений начальной и конечной точек
этого пути и не зависит от формы пути.
На рис.1.1.18
работа на пути
![]() равна работе на пути
равна работе на пути![]() :
избыточная работа, совершаемая на пути
:
избыточная работа, совершаемая на пути![]() при перемещении пробного заряда за
пределы сферы радиуса
при перемещении пробного заряда за
пределы сферы радиуса![]() ,
компенсируется отрицательной работой,
совершаемой при последующем приближении
пробного заряда к заряду
,
компенсируется отрицательной работой,
совершаемой при последующем приближении
пробного заряда к заряду![]() на последнем участке пути
на последнем участке пути![]() .
Таким образом, поле неподвижного
точечного заряда есть поле потенциальное.
.
Таким образом, поле неподвижного
точечного заряда есть поле потенциальное.
Очевидно, сумма потенциальных полей тоже есть потенциальное поле (так как если работа слагаемых сил не зависит от формы пути, то и работа равнодействующей от нее не зависит). Поле произвольной системы зарядов можно рассматривать как сумму полей каждого из точечных зарядов, поэтому всякое электростатическое поле есть поле потенциальное.
Согласно
интегральной форме теоремы Стокса
циркуляция векторного поля равна
![]() ,
тогда
проекция
,
тогда
проекция
![]() на произвольное направление поля
на произвольное направление поля![]() равна
равна![]() ,
где
,
где![]() - бесконечно малая площадка, проходящая
через точку
- бесконечно малая площадка, проходящая
через точку![]() перпендикулярно вектору
перпендикулярно вектору![]() .
.
Так
как циркуляция вектора
![]() по замкнутому контуру равна нулю,
по замкнутому контуру равна нулю,![]() ,
то
,
то![]() ,
или
,
или
![]() .
(1.1.4)
.
(1.1.4)
Так
как направление
![]() выбрано произвольно, то проекция
выбрано произвольно, то проекция![]() на любые направления равна 0, поэтому
из (1.1.4)
на любые направления равна 0, поэтому
из (1.1.4)![]() во
всех точках электростатического поля,
то есть электростатическое поле является
безвихревым.
Это дифференциальная форма теоремы
Стокса для электростатического поля.
Выражения (1.1.3) и (1.1.4) эквивалентны.
во
всех точках электростатического поля,
то есть электростатическое поле является
безвихревым.
Это дифференциальная форма теоремы
Стокса для электростатического поля.
Выражения (1.1.3) и (1.1.4) эквивалентны.
