MATAN
.docx1)Последовательность
и ее предел.
Пусть имеется правило, по которому
каждому натуральному n
ставится в соответствие вещественное
число
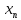 :n
:n В этом случае говорят, что задана
последовательность x1,x2,x3…
Её обозначают {
В этом случае говорят, что задана
последовательность x1,x2,x3…
Её обозначают {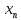 }.
При этом число
}.
При этом число
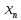 называют n-ым
членом или общим членом последовательности
{
называют n-ым
членом или общим членом последовательности
{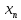 }.
Примеры: 1,2,3,4…
}.
Примеры: 1,2,3,4…
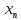 =n;
=n;
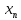 +∞;
-1,-2,-3…
+∞;
-1,-2,-3…
 =-n;
=-n;
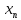 -∞;-1,1,-1,1,-1…
-∞;-1,1,-1,1,-1…
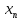 =(-1)^n.
(Никуда не стремится)
=(-1)^n.
(Никуда не стремится)
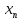 a,
если
a,
если
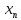 неограниченно приближается к а с ростом
n.Определение
таково:
неограниченно приближается к а с ростом
n.Определение
таково:
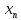 a
при n→∞
или, что
тоже самое
a
при n→∞
или, что
тоже самое
 если для любого ε>0 сущ.такое N=N(ε)
такое, что |
если для любого ε>0 сущ.такое N=N(ε)
такое, что |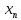 -a|<ε
для любого n>N.
Другими словами
-a|<ε
для любого n>N.
Другими словами
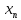 →
a(n→∞)
если для любой окрестности точки a
найдется номер, начиная с которого все
члены последовательности принадлежат
этой окрестности. Последовательность
{
→
a(n→∞)
если для любой окрестности точки a
найдется номер, начиная с которого все
члены последовательности принадлежат
этой окрестности. Последовательность
{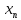 }
называется бесконечно малой если
}
называется бесконечно малой если
 →0
при n→∞
→0
при n→∞
2)
Существование предела для монотонной
ограниченной последовательности. Число
e.Экспонента
и натуральный логарифм. Говорят,
что последовательность {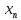 }
монотонно возрастает(не убывает) если
}
монотонно возрастает(не убывает) если
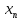 <
< для каждого n(
для каждого n(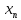 =<
=< для каждого n).
Говорят, что последовательность {
для каждого n).
Говорят, что последовательность { }
ограничена сверху, если существует
такое M>0
такое, что
}
ограничена сверху, если существует
такое M>0
такое, что
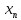 =<M
для любого n(аналогично
для убывающей последовательности и
ограниченной снизу). Теорема: монотонно
возрастающая( или неубывающая) ограниченная
сверху последовательность имеет конечный
предел. Если для всех n
=<M
для любого n(аналогично
для убывающей последовательности и
ограниченной снизу). Теорема: монотонно
возрастающая( или неубывающая) ограниченная
сверху последовательность имеет конечный
предел. Если для всех n
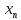 =<
=< и
и
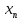 =<M,
то существует такой
=<M,
то существует такой
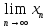 =a,
a=<M.
Число e.
=a,
a=<M.
Число e.

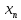 <
<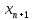 для каждого n
и что
для каждого n
и что
 <3
для любого n
(следовательно) существует предел
последовательности, обозначаемый e.
<3
для любого n
(следовательно) существует предел
последовательности, обозначаемый e.
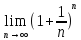 =e≈2,7.
=e≈2,7.
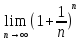 есть неопределенность типа
есть неопределенность типа
 .Ф-ция.
Y=
.Ф-ция.
Y=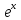 называется экспонентой и обозначается
exp(x).Логарифм
с основанием e
называется натуральным логарифмом и
обозначается ln(x)
называется экспонентой и обозначается
exp(x).Логарифм
с основанием e
называется натуральным логарифмом и
обозначается ln(x)
3)Понятие
функции. Область определения, область
значения. Пусть
заданы X
и Y
два множества. Говорят, что задана
функция(отображения) f
из X
в Y(и
пишут f:X→Y),
если задано правило, согласно которому
каждому элементу x X
однозначно ставится в соответствие
элемент y
X
однозначно ставится в соответствие
элемент y Y.
Обозначают y=f(x)
и называют образом элемента x
при отображении f,
а x
называют прообразом элемента y
при этом отображении. Также произвольный
элемент x
Y.
Обозначают y=f(x)
и называют образом элемента x
при отображении f,
а x
называют прообразом элемента y
при этом отображении. Также произвольный
элемент x X
называют аргументом ф-ции f(x).
Множество X
называют областью определения, а
множество Y
областью значений ф-ции f.
Множество образом f(x)
всех элементов x
X
называют аргументом ф-ции f(x).
Множество X
называют областью определения, а
множество Y
областью значений ф-ции f.
Множество образом f(x)
всех элементов x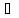 X
обозначают f(X)
т.е. f(X)={y=f(x)|x
X
обозначают f(X)
т.е. f(X)={y=f(x)|x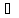 X}
X}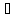 Y.
Графиком ф-ции f:
X→Y
называется множество пар (x;
y)
таких, что x
Y.
Графиком ф-ции f:
X→Y
называется множество пар (x;
y)
таких, что x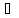 X,
а y=f(x).
Если X
и Y-подмножества
числовой оси, то график располагается
на плоскости
X,
а y=f(x).
Если X
и Y-подмножества
числовой оси, то график располагается
на плоскости
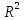
4)
Обратные функции. Функция
называется строго монотонно возрастающей
на отрезке
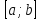 ,
если из условий x1,x2
,
если из условий x1,x2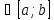 ,x1<x2
следует что f(x1)<f(x2).
Аналогично определяется строго монотонно
убывающая на отрезке функция. Функция
строго монотонна на отрезке, если оно
монотонно возрастает или монотонно
убывает на этом отрезке. Сложная
функция.
Пусть даны 3 множества X,Y,Z
и два отображения f:X→Y
и g:Y→Z.
Можно построить отображение из X
в Z
по правилу z=g(f(x))
для любого x
,x1<x2
следует что f(x1)<f(x2).
Аналогично определяется строго монотонно
убывающая на отрезке функция. Функция
строго монотонна на отрезке, если оно
монотонно возрастает или монотонно
убывает на этом отрезке. Сложная
функция.
Пусть даны 3 множества X,Y,Z
и два отображения f:X→Y
и g:Y→Z.
Можно построить отображение из X
в Z
по правилу z=g(f(x))
для любого x X,
т.е. элементу x
отображение f
сопоставляет элемент y=f(x)
а элементу y
отображение g
сопоставляет элемент z=g(y)=g(f(x))
Тем самым определена ф-ция F:X→Z,
что F(x)=g(f(x))
для любого x
X,
т.е. элементу x
отображение f
сопоставляет элемент y=f(x)
а элементу y
отображение g
сопоставляет элемент z=g(y)=g(f(x))
Тем самым определена ф-ция F:X→Z,
что F(x)=g(f(x))
для любого x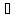 X.
Обозначается F=g
X.
Обозначается F=g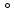 f
и называется сложной ф-цией или
суперпозицией отображений f
и g.
Обратная
функция.
Пусть f:X→Y
биекция. Построим отображение из Y
в X
следующим образом. Возьмем произвольный
элемент y
f
и называется сложной ф-цией или
суперпозицией отображений f
и g.
Обратная
функция.
Пусть f:X→Y
биекция. Построим отображение из Y
в X
следующим образом. Возьмем произвольный
элемент y Y.Поскольку
f
отображает «на»,
то у него
имеется прообраз x,т.е.
такой элемент, что f(x)=y.
Этот прообраз является единственным,
поскольку отображение в f
взаимно-однозначно. Произвольному y
Y.Поскольку
f
отображает «на»,
то у него
имеется прообраз x,т.е.
такой элемент, что f(x)=y.
Этот прообраз является единственным,
поскольку отображение в f
взаимно-однозначно. Произвольному y Y
мы сопоставили единственный x
Y
мы сопоставили единственный x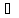 X.
Обозначим его x=g(y).Получили
отображение g:
Y→X
которое называется обратным к отображению
f:X→Y
и обозначается g=
X.
Обозначим его x=g(y).Получили
отображение g:
Y→X
которое называется обратным к отображению
f:X→Y
и обозначается g=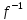 .
При этом для x
.
При этом для x X
и y
X
и y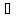 Y
имеем x=g(y)↔y=f(x);
g(f(x))=x
для всех x
Y
имеем x=g(y)↔y=f(x);
g(f(x))=x
для всех x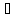 X;
f(g(y))=y
для всех y
X;
f(g(y))=y
для всех y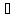 Y.
На примере sin(x)
выберем отрезок
Y.
На примере sin(x)
выберем отрезок
 -симметричен
относительно нуля, на нем синус принимает
все свои значения и сохраняет нечетность.
Sin:
-симметричен
относительно нуля, на нем синус принимает
все свои значения и сохраняет нечетность.
Sin: →
→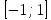 биекция(след.)
сущ.-вует. обратная ф-ция arcsin
биекция(след.)
сущ.-вует. обратная ф-ция arcsin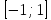 →
→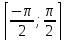 .Если
x
.Если
x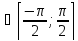 ,y
,y то
arcsin(y)=x↔y=sin(x);arcsin(sin(x))=x
для любого x
то
arcsin(y)=x↔y=sin(x);arcsin(sin(x))=x
для любого x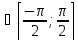 ;
sin(arcsin(y))=y
для любого y
;
sin(arcsin(y))=y
для любого y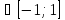 .
Лог.функция.
.
Лог.функция.
 (a>0;a≠1)
При x>0
(a>0;a≠1)
При x>0
 ↔
↔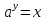 ,т.е.
лог.ф-ция является обратной к показательной.
,т.е.
лог.ф-ция является обратной к показательной.
5)Предел
функции в точке. Теоремы о пределах.
Пусть y=f(x)
определена в некоторой окрестности
точки a
за исключением быть может самой точки
a.
Запись =b
означает, что f(x)
неограниченно приближается к b
по мере того как xк
a.
Точное определение таково:
=b
означает, что f(x)
неограниченно приближается к b
по мере того как xк
a.
Точное определение таково:
 =b
если для каждого ε>0 существует такое
=b
если для каждого ε>0 существует такое
 такое, что из условий 0<|x-a|<
такое, что из условий 0<|x-a|<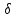 следует что |f(x)-b|<ε.
B
есть предел ф-ции f(x)
в точке a
если для любой окрестности V
точки b
существует окрестность U
точки a
такая, что из условий x
следует что |f(x)-b|<ε.
B
есть предел ф-ции f(x)
в точке a
если для любой окрестности V
точки b
существует окрестность U
точки a
такая, что из условий x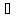 U,x≠a
следует что f(x)
U,x≠a
следует что f(x) V.
Теоремы о
пределах: 1)Единственность
предела: если
V.
Теоремы о
пределах: 1)Единственность
предела: если
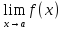 =b1
=b1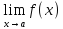 =b2
то b1=b2.
Док-во: пусть b1≠b2
ε=(b2-b1)/3
(следоват.) окрестности V1=(b1-ε,b1+ε)
и V2=(b2-ε,b2+ε)
не пересекаются. Поскольку
=b2
то b1=b2.
Док-во: пусть b1≠b2
ε=(b2-b1)/3
(следоват.) окрестности V1=(b1-ε,b1+ε)
и V2=(b2-ε,b2+ε)
не пересекаются. Поскольку
 =b1
то для указанного ε найдется
=b1
то для указанного ε найдется
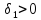 такое, что неравенства 0<|x-a|<
такое, что неравенства 0<|x-a|<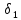 влекут условие f(x)
влекут условие f(x) .
Поскольку
.
Поскольку
 =b2
то для указанного ε найдется
=b2
то для указанного ε найдется
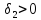 такое, что неравенства 0<|x-a|<
такое, что неравенства 0<|x-a|< влекут условие f(x)
влекут условие f(x)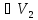 .
Положим
.
Положим
 min{
min{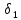 ;
; }
тогда из равенств 0<|x-a|<
}
тогда из равенств 0<|x-a|<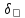 должны следовать оба условия f(x)
должны следовать оба условия f(x) и f(x)
и f(x)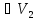 что невозможно поскольку V1
что невозможно поскольку V1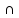 V2=
V2= .Утверждение
теоремы из полученного противоречия.
Пусть для ф-ций f
и g
существуют пределы
.Утверждение
теоремы из полученного противоречия.
Пусть для ф-ций f
и g
существуют пределы
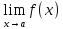 =A;
=A; =B.
Справедливы утверждения: 2)Предел суммы
f+g
сущ-вует. и равен сумме пределов:
=B.
Справедливы утверждения: 2)Предел суммы
f+g
сущ-вует. и равен сумме пределов:
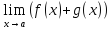 =A+B;
=A+B; .
3)Предел произведения существует и =
произведению пределов:
.
3)Предел произведения существует и =
произведению пределов:
 4)Предел частного f/g
сущ-вует и равен частному от пределов:
4)Предел частного f/g
сущ-вует и равен частному от пределов:
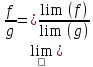 при
при
 .
5)Пусть f(x)=<g(x)
в окрестности точки a.
Тогда
.
5)Пусть f(x)=<g(x)
в окрестности точки a.
Тогда
 т.е.неравенство передается и предельным
величинам. 6)Т.о пределе сложной ф-ции:
Пусть
т.е.неравенство передается и предельным
величинам. 6)Т.о пределе сложной ф-ции:
Пусть
 и пусть
и пусть
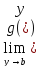 =c
тогда
=c
тогда
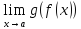 =c
=c
6)Бесконечно
малые величины (для ф-ции). Сравнение их
по порядку малости. Эквивалентные б.м.
Ф-ция α(x)
называется бесконечно малой при x→a
если
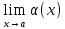 =0.
Например x,sin(x),1-cos(x),ln(1+x)-б.м.
Теорема α(x)
и β(x)-б.м.
при xa
(следоват.) α(x)+β(x);
α(x)*β(x)-б.м.
при xa.
Док-во: α(x)+β(x)=γ(x)-б.м.
при xa
Пусть ε>0; существует
=0.
Например x,sin(x),1-cos(x),ln(1+x)-б.м.
Теорема α(x)
и β(x)-б.м.
при xa
(следоват.) α(x)+β(x);
α(x)*β(x)-б.м.
при xa.
Док-во: α(x)+β(x)=γ(x)-б.м.
при xa
Пусть ε>0; существует
 >0
такое, что |α(x)|<
>0
такое, что |α(x)|<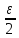 при |x-a|<
при |x-a|<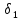 (поскольку
α - б.м. при xa)
Далее существует такое
(поскольку
α - б.м. при xa)
Далее существует такое
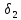 >0
такое что |β(x)|<
>0
такое что |β(x)|<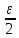 при |x-a|<
при |x-a|<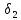 (поскольку
β - б.м. при xa)
Положим
(поскольку
β - б.м. при xa)
Положим
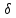 =min{
=min{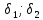 }
тогда из условия |x-a|<
}
тогда из условия |x-a|<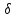 следует, что |γ(x)|=|α(x)+β(x)|
следует, что |γ(x)|=|α(x)+β(x)|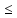 |α(x)|+|β(x)|<
|α(x)|+|β(x)|<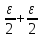 =ε. Для произвольного ε>0 мы указали
=ε. Для произвольного ε>0 мы указали
 >0
такое, что из условия |x-a|<
>0
такое, что из условия |x-a|<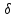 следует что |γ(x)|<ε
γ=α+β-б.м. при xa
Лемма
следует что |γ(x)|<ε
γ=α+β-б.м. при xa
Лемма
 =
b
тогда и только тогда когда f(x)=b+α(x)
где α(x)-б.м.
при xa.
Сравнение
б.м. Пусть
α(x)
и β(x)-б.м.
при xa
и пусть α(x)≠0
в окрестности точки a.
Говорят, что β есть величина более
высокого порядка малости(и пишут β=о(α))
чем α, если
=
b
тогда и только тогда когда f(x)=b+α(x)
где α(x)-б.м.
при xa.
Сравнение
б.м. Пусть
α(x)
и β(x)-б.м.
при xa
и пусть α(x)≠0
в окрестности точки a.
Говорят, что β есть величина более
высокого порядка малости(и пишут β=о(α))
чем α, если
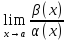 =0.
Другими словами
=0.
Другими словами
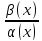 =γ(x)
есть б.м. при xa
и тогда β(x)=
γ(x)*α(x).
Таблица эквивалентностей.
Sin(x)
=γ(x)
есть б.м. при xa
и тогда β(x)=
γ(x)*α(x).
Таблица эквивалентностей.
Sin(x) x;tg(x)
x;tg(x) x;1-cos(x)
x;1-cos(x) x*x/2;
x*x/2; ;
;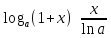 ;
; ;
arcsin(x)
;
arcsin(x) x;arctg(x)
x;arctg(x) x;
x;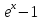 x;
x;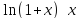 ;
;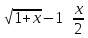
7)1-ый
замечательный предел.
 =1
sinx~x
Док-во: OA=1
дугаAB=x;
AC=tgx;
S(oab)=1/2OA*OB*sinx=1/2sinx;
Sсектора(OAB)=1/2r*r*x=1/2x;
S(oac)=1/2tgx;1/2sinx<1/2x<1/2tgx;
=1
sinx~x
Док-во: OA=1
дугаAB=x;
AC=tgx;
S(oab)=1/2OA*OB*sinx=1/2sinx;
Sсектора(OAB)=1/2r*r*x=1/2x;
S(oac)=1/2tgx;1/2sinx<1/2x<1/2tgx;
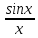 <1;
cosx<
<1;
cosx<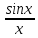 <1;
cosx1
при x0
<1;
cosx1
при x0
8)Бесконечно
большая величина. Связь между бесконечно
малыми и бесконечно большими величинами.
Последовательность
{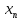 }
называется бесконечно большой если
}
называется бесконечно большой если
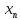 +∞
при n∞.
Ф-ция называется бесконечно большой
при xa
если
+∞
при n∞.
Ф-ция называется бесконечно большой
при xa
если
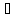 N>0
N>0
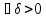 такое что 0<|x-a|<
такое что 0<|x-a|< (следоват.)|f(x)|>N.Это
определение дано для конечного a.Если
f(x)-б.б.
при xa
то 1/f(x)-б.м.
при xa
т.е. 1/б.б=б.м. Если f(x)-б.м.при
xa
и f(x)≠0
в окрестностях точки a
при x≠a
то 1/f(x)-б.б.
при xa.
1/б.м=б.б.(б.м.≠0)
(следоват.)|f(x)|>N.Это
определение дано для конечного a.Если
f(x)-б.б.
при xa
то 1/f(x)-б.м.
при xa
т.е. 1/б.б=б.м. Если f(x)-б.м.при
xa
и f(x)≠0
в окрестностях точки a
при x≠a
то 1/f(x)-б.б.
при xa.
1/б.м=б.б.(б.м.≠0)
9)Ограниченная
величина. Произведение б.м. на ограниченную.
Ф-ция f(x)
называется ограниченной на множестве
A
если существует число M>0
такое что |f(x)|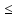 M
M
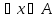 .
Пусть ω(x)
определена в окрестности точки a
за исключением самой точки a.
Ф-ция ω(x)
называется ограниченной при xa
если существует окрестность U
точки a
и число M>0
такое что |f(x)|
.
Пусть ω(x)
определена в окрестности точки a
за исключением самой точки a.
Ф-ция ω(x)
называется ограниченной при xa
если существует окрестность U
точки a
и число M>0
такое что |f(x)|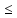 M
M
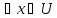 ,
x≠a,
т.е. f
ограничена на U\{a}.
Пусть α(x)-б.м.
при xa,
а ω(x)
ограниченная величина при xa.
Тогда α(x)ω(x)-б.м.
при xa
т.е. (б.м.)*(огранич.)=(б.м.)
,
x≠a,
т.е. f
ограничена на U\{a}.
Пусть α(x)-б.м.
при xa,
а ω(x)
ограниченная величина при xa.
Тогда α(x)ω(x)-б.м.
при xa
т.е. (б.м.)*(огранич.)=(б.м.)
11)Левые
и правые пределы функции в точке. Запись
xa+0
означает что xa
и x>a
т.е. xa
справа. Запись xa-0
означает что xa
и x<a,
т.е. xa
слева. По определению
 =
= если
если
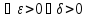 такое
что a-
такое
что a-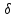 <x<a
(след.) |f(x)-
<x<a
(след.) |f(x)-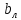 |<ε
Величину
|<ε
Величину
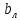 называют левым пределом ф-ции f
в точке a
и обозначают f(a-0)
По определению
называют левым пределом ф-ции f
в точке a
и обозначают f(a-0)
По определению
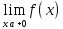 =
=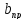 если
если
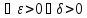 такое
что a<x<a+
такое
что a<x<a+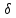 (след.) |f(x)-
(след.) |f(x)-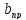 |<ε
Величину
|<ε
Величину
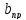 называют правым пределом ф-ции f
в точке a
и обозначают f(a+0).
Разность f(a+0)-f(a-0)
называют скачком функции f
в точке a.
Существование предела A=
называют правым пределом ф-ции f
в точке a
и обозначают f(a+0).
Разность f(a+0)-f(a-0)
называют скачком функции f
в точке a.
Существование предела A=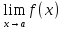 равносильно тому, что существует левый
предел f(a-0),
существует правый предел f(a+0)
и они равны между собой: f(a-0)=f(a+0).
Их общее значение и есть предел функции
f
в точке a.
равносильно тому, что существует левый
предел f(a-0),
существует правый предел f(a+0)
и они равны между собой: f(a-0)=f(a+0).
Их общее значение и есть предел функции
f
в точке a.
12)Задача
о непрерывном начислении процентов.
При решении
этой задачи используем 1 замечательный
предел.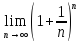 .
Пусть первоначальный вклад в банк
.
Пусть первоначальный вклад в банк
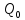 средств. Банк выплачивает ежегодно p%
годовых. Найти размер вклада через t
лет. Через год величина вклада станет
равной Q1=
средств. Банк выплачивает ежегодно p%
годовых. Найти размер вклада через t
лет. Через год величина вклада станет
равной Q1= .
Через t
лет вклад окажется равным
.
Через t
лет вклад окажется равным
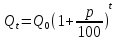 Это основная формула для вычисления
сложных процентов. Величина вклада за
t
лет при nt
начислениях составит
Это основная формула для вычисления
сложных процентов. Величина вклада за
t
лет при nt
начислениях составит
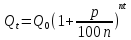 Величина вклада растет не беспредельно.
Следует перейти к пределу.
Величина вклада растет не беспредельно.
Следует перейти к пределу.
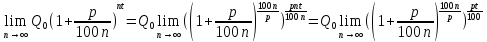 Поскольку x=
Поскольку x=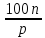 ∞
то в силу 1-ого замечательного предела
имеем
∞
то в силу 1-ого замечательного предела
имеем
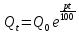 .
Это показательный(экспотенциальный)
закон роста вклада при непрерывном
начислении процентов.
.
Это показательный(экспотенциальный)
закон роста вклада при непрерывном
начислении процентов.
13)Непрерывность
функции в точке. Приращение функции.
Непрерывность элементарных функций.
Пусть функция
y=f(x)
определена в окрестности точки x0.
Функция f(x)
называется непрерывной в точке x0
если существует предел функции при xx0
и он равен значению функции в этой
точке: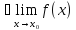 =f(x)=f(
=f(x)=f(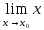 )
Следовательно, для непрерывной функции
знак ф-ции и знак предела можно менять
местами. Эквивалентное определение
непрерывности в точке. Пусть
)
Следовательно, для непрерывной функции
знак ф-ции и знак предела можно менять
местами. Эквивалентное определение
непрерывности в точке. Пусть
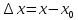 (x=
(x=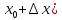 и назовем
и назовем
 приращением аргумента. Ему соответствует
приращением аргумента. Ему соответствует
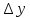 приращение
функции:
приращение
функции:
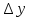 =
=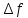 =f(
=f(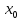 +
+ )-f(
)-f( показывает изменение ф-ции при изменении
аргумента. Непрерывность ф-ции в точке
показывает изменение ф-ции при изменении
аргумента. Непрерывность ф-ции в точке
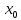 эквивалентна условию
эквивалентна условию
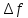 0
при
0
при
 x0:
приращение функции стремится к нулю,
когда приращение аргумента стремится
к нулю. Ф-ция непрерывна в точке
x0:
приращение функции стремится к нулю,
когда приращение аргумента стремится
к нулю. Ф-ция непрерывна в точке
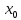 если
если
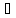 f(
f(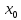 -0),
-0),
 f(
f(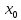 +0)
и f(
+0)
и f(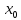 +0)=f(
+0)=f(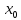 -0)=f(
-0)=f( ).
Ф-ция называется непрерывной слева в
точке
).
Ф-ция называется непрерывной слева в
точке
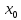 если
если
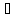 f(
f(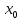 -0)
и f(
-0)
и f( -0)=f(
-0)=f(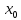 ).
Ф-ция называется непрерывной справа в
точке
).
Ф-ция называется непрерывной справа в
точке
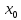 если
если
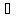 f(
f(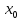 +0)
и f(
+0)
и f(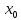 +0)=f(
+0)=f( )
)
14)Сумма,
произведение и частное непрерывных
функций. Непрерывность сложной функции.
Теорема:
пусть f(x)
и g(x)
непрерывны в точке
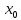 .
Тогда функции f(x)
.
Тогда функции f(x)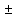 g(x)
f(x)*g(x),
g(x)
f(x)*g(x),
 непрерывны в точке
непрерывны в точке
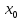 .
В последнем случае предполагается, что
g(
.
В последнем случае предполагается, что
g(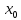 )≠0.
Итак, сумма, разность, произведение и
частное (знаменатель не 0) непрерывных
ф-ций есть непрерывная ф-ция. Теорема
(о непрерывности сложной ф-ции). Пусть
y=f(x)
непрерывна в точке
)≠0.
Итак, сумма, разность, произведение и
частное (знаменатель не 0) непрерывных
ф-ций есть непрерывная ф-ция. Теорема
(о непрерывности сложной ф-ции). Пусть
y=f(x)
непрерывна в точке
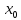 ,
а z=g(y).
Пусть y0=f(
,
а z=g(y).
Пусть y0=f( ).
Тогда сложная ф-ция z=g(f(x))
непрерывна в точке
).
Тогда сложная ф-ция z=g(f(x))
непрерывна в точке
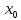 .
Любая элементарная ф-ция непрерывна в
каждой точке своей области определения(если
эта точка является концом отрезка, то
имеется в виду непрерывность слева или
справа).
.
Любая элементарная ф-ция непрерывна в
каждой точке своей области определения(если
эта точка является концом отрезка, то
имеется в виду непрерывность слева или
справа).
15)Разрыв
1-ого рода(устранимый и нет). Разрыв 2-ого
рода. Примеры. Пусть
f(x)
определена в окрестности точки
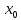 за исключением быть может самой
за исключением быть может самой
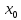 .
Разрыв в точке
.
Разрыв в точке
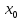 означает, что одно из условий
означает, что одно из условий
 f(
f( -0)
-0)
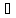 f(
f( +0)
и f(
+0)
и f(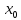 +0)=f(
+0)=f( -0)=f(
-0)=f(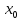 )
в точке
)
в точке
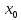 нарушено или вообще ф-ция в
нарушено или вообще ф-ция в
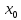 не определена. В точке
не определена. В точке
 имеется разрыв 1-ого рода, если существуют
конечные пределы f(
имеется разрыв 1-ого рода, если существуют
конечные пределы f(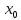 -0)
и f(
-0)
и f(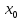 +0)
но нарушено одно из равенств
f(
+0)
но нарушено одно из равенств
f( +0)=f(
+0)=f(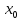 -0)=f(
-0)=f(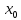 ).
Разрыв устранимый, если левый и правый
предел в точке
).
Разрыв устранимый, если левый и правый
предел в точке
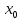 совпадают f(
совпадают f( +0)=f(
+0)=f(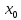 -0)
Устранить такой разрыв можно переопределив
или доопределив f
в точке
-0)
Устранить такой разрыв можно переопределив
или доопределив f
в точке
 ,
чтобы выполнялось f(
,
чтобы выполнялось f(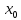 +0)=f(
+0)=f(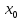 -0)=f(
-0)=f(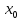 ).
Разрыв неустранимый если f(
).
Разрыв неустранимый если f(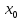 +0)≠f(
+0)≠f( -0)
Точка
-0)
Точка
 называется точкой разрыва второго рода,
если не существует конечного левого
предела f(
называется точкой разрыва второго рода,
если не существует конечного левого
предела f(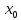 -0)
или конечного правого предела f(
-0)
или конечного правого предела f( +
0) или обоих. Y=
+
0) или обоих. Y=
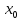 =1
устранимый разрыв 1 рода. Y=1/x
при x=0
разрыв 2 рода.
=1
устранимый разрыв 1 рода. Y=1/x
при x=0
разрыв 2 рода.
16)Непрерывность
функции на отрезке. Теорема Вейерштрасса.
Т. О промежуточном значении. Ф-ция
y=f(x)
называется непрерывной на интервале
(a;b)
если она непрерывна в каждой точке x
этого интервала. Ф-ция y=f(x)
называется непрерывной на отрезке [a;b]
если она непрерывна на интервале (a;b),
а также непрерывна справа в точке a
и непрерывна слева в точке b.
Т.Вейерштрасса.
Ф-ция f(x)
непрерывна на отрезке [a;b]
достигает на этом отрезке наибольшего
и наименьшего значений, т.е.
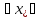 [a;b]
такая, что f(x)
[a;b]
такая, что f(x)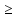 f(
f(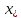 )
)
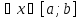 (минимум)
(минимум)
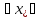 [a;b]
такая, что f(x)
[a;b]
такая, что f(x)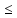 f(
f( )
)
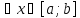 (максимум)
(максимум)
 минимальное
и максимальное значение. Т.о
промежуточном значении: непрерывная
на [a;b]
ф-ция принимает любое промежуточное
значение между минимальным и максимальным,
т.е.
минимальное
и максимальное значение. Т.о
промежуточном значении: непрерывная
на [a;b]
ф-ция принимает любое промежуточное
значение между минимальным и максимальным,
т.е.
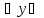 [
[ ]
]
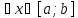 такое, что y=f(x)
такое, что y=f(x)
17)Определение
производной и дифференциала. Геометрич.
Смысл производной и дифференциала.
Связь между приращением функции и
дифференциалом. Левая и правая производные.
Пусть y=f(x)
определена в окрестности
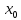 (включая
(включая
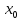 ).
Говорят, что функция дифференцируема
в точке
).
Говорят, что функция дифференцируема
в точке
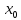 ,
если существует предел отношения
приращения ф-ции ∆f
к приращению аргумента при условии, что
∆x0.
,
если существует предел отношения
приращения ф-ции ∆f
к приращению аргумента при условии, что
∆x0.
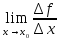 =
=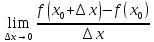 .
Величина предела называется производной
ф-ции в точке
.
Величина предела называется производной
ф-ции в точке
 и обозначается f’(
и обозначается f’(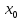 );
f’(
);
f’(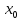 )=
)=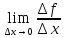 ;
;
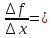 f’(
f’(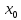 )+α(
)+α(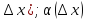 0;
при
0;
при
 x0(следоват.)
x0(следоват.)
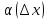 - б.м.; ∆f=f’(
- б.м.; ∆f=f’( +
+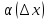 ∆x.
Величина f’(
∆x.
Величина f’(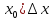 линейно зависит от приращения аргумента
∆x.
Её называют дифференциалом ф-ции f
в точке
линейно зависит от приращения аргумента
∆x.
Её называют дифференциалом ф-ции f
в точке
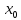 и обозначают df;
df=
f’(
и обозначают df;
df=
f’(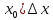 где dx=∆x.
Геометрический
смысл: f’(
где dx=∆x.
Геометрический
смысл: f’(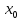 )=
)=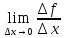 =tg(
=tg( ).
Производная это тангенс угла наклона
касательной к графику в точке (
).
Производная это тангенс угла наклона
касательной к графику в точке (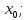 f(
f(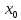 ))
Дифференциал df
есть приращение ординаты касательной
(геометрический смысл дифференциала).
Левая производная y=f(x)
в точке
))
Дифференциал df
есть приращение ординаты касательной
(геометрический смысл дифференциала).
Левая производная y=f(x)
в точке
 это предел
это предел
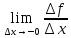 ;
правая производная
;
правая производная

18)Производные
суммы, произведения и частного. Пусть
u=u(x)
и v=v(x)
дифференцируемые функции. 1)(u+v)’=u’+v’
2)(cu)’=cu’
3)(uv)’=u’v+v’u
4)(u/v)’=(u’v-v’u/v*v)(v≠0)
1)∆(u+v)=(u(x+∆x)+v(x+∆x))-(u(x)+v(x))=(u(x+∆x)-u(x))+(v(x+∆x)-v(x))=
∆u+∆v
2) ∆(cu)=c(∆u)
3)
∆(uv)=u(x+∆x)*v(x+∆x)-u(x)*v(x)=(u(x+∆x)-u(x))*v(x+∆x)+u(x)(v(x+∆x)-v(x))=
∆u*v(x+∆x)+u(x)*
∆v;
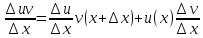 далее
перейти к пределу по ∆x0
далее
перейти к пределу по ∆x0
19)Таблица
производных. Вывод формул для синуса и
квадратичной ф-ции. Для
синуса y=sin(x)
∆y=sin(x+∆x)-sin(x)=2sin(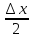 )*cos(x+
)*cos(x+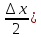 (разность
синусов) y’=
(разность
синусов) y’=
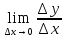 =
=
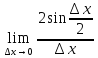 cos(x+
cos(x+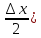 ;
;
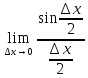 =
=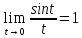 (1
замечательный предел) В силу непрерывности
функции y=cos(x)
имеем
(1
замечательный предел) В силу непрерывности
функции y=cos(x)
имеем
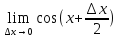 =cos(x);
y’(x)=cos(x);
(sin(x))’=cos(x).
Для квадратичной ф-ции. y=x*x;
∆y=(x+∆x)^2-x*x=∆x(2x+∆x)
(разность квадратов) y’=
=cos(x);
y’(x)=cos(x);
(sin(x))’=cos(x).
Для квадратичной ф-ции. y=x*x;
∆y=(x+∆x)^2-x*x=∆x(2x+∆x)
(разность квадратов) y’=
 =
=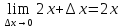 ;
(x*x)’=2x
Таблица производных. С’=0;
x’=1; (
;
(x*x)’=2x
Таблица производных. С’=0;
x’=1; (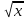 )=
)=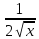 ;
(
;
( )’=-
)’=-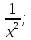 (
(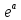 )’=a
)’=a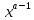 ;
;
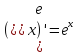 ;
(
;
( )’=
)’=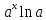 ;
(
;
(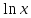 )’=
)’=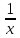 ;
;
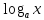 =
= ;
(sin(x))’=cos(x); (cos(x))’=-sin(x); tg(x)’=
;
(sin(x))’=cos(x); (cos(x))’=-sin(x); tg(x)’=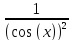 ;
ctg(x)=-
;
ctg(x)=-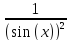 ;
(arcsin(x))’=
;
(arcsin(x))’=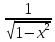 ;
(arccos(x))’=-
;
(arccos(x))’=-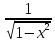 ;
(arctg(x))’=
;
(arctg(x))’= ;
(arcctg(x))’=-
;
(arcctg(x))’=-