Символический язык содержательных теорий множеств

В процессе изучения курса будем различать объектный язык теории множеств и метаязык, средствами которого изучается объектный язык.

Под языком теории множеств будем понимать реляционную систему, основным множеством которой являются символы алфавита A, а отношения позволяют получать синтаксически правильные языковые выражения, среди которых выделяют формулы F.

В этом плане L = ‹A,B›, BAA² ... Aⁿ, FB.

Логическая экспликация понятия подмножества А мн-ва М с агрегатной и атрибутивной точек зрения следующая:

(AM)  (х((xA)  (xM))) (1)

(AM)  (x((xA)  (xM))) (2)

здесь метасимволы  и  следует считать соответственно как "эквивалентность" и "если…то".

Примеры.

1. Множество всех четных целых чисел. М = { для некоторого }

2. Множество натуральных чисел. .

Если М_а М_b, но М_а иМ_а М_b, то М_а является собственным подмножеством в М_b. Таким образом, если множество М' - подмножество множества М, а множество М не является подмножеством множества М', то множество М' называется собственным подмножеством множества М.

Для обозначения этого факта будем использовать двойной знак включения подмножеств , т.е. писать .

ТЕОРЕМА Множество, имеющее бесконечное подмножество, бесконечно:

.

доказательство

Множество В бесконечно, значит, , причем . Далее, |В| = |С|, то есть существует взаимно-однозначное соответствие В ~ С из множества В в его собственное подмножество С. Обозначим это соответствие х → х'. Построим соответствие из множества А в его собственное подмножество:

then х' else х end if .

Другими словами, на элементах из В мы пользуемся заданным соответствием, а остальным элементам сопоставлям их самих. Это взаимно-однозначное соответствие из множества А в его собственное подмножество, и значит |А| = ∞.

СЛЕДСТВИЕ Все подмножества конечного множества конечны

Добавление и удаление элементов

Если А — множество, а х — элемент, причем , то элемент х можно добавить в А:

.

Аналогично, если А — множество, а x - элемент, причем , то элемент х можно удалить из А:

.

Легко видеть, что при удалении и добавлении конечного числа элементов конечные множества остаются конечными, а бесконечные — бесконечными.

Операции добавления и удаления элементов являются частными случаями операций объединения и разности, и потому, строго говоря, излишни. В стандартных учебниках по теории множеств такие операции не рассматриваются и не упоминаются. Здесь они введены для упрощения обозначений. Такой подход акцентирует «программистское» отношение к математике: мы сводим новые операции, если это практически удобно, даже если это теоретически излишне.

Булеан и универсумом

Для каждого множества М существует множество, элементами которого являются подмножества множества М и только они. Такое множество будем называть семейством множества М или булеаном этого множества и обозначать В(М), а множество М — универсальным, универсумом или пространством и обозначать 1.

Пример.

Образовать булеан В(1) от универсума 1 = {у, х, а}.

Решение. Первым множеством является пустое множество , не содержащее ни одного элемента. Затем образуем множества, содержащие по одному элементу – их будет равно числу сочетаний, затем множества, содержащих по два элемента, которых будет, и, наконец, множество, содержащее все элементы множества1. В рассматриваемом случае

В(1)= {,{у}, {х}, {а}, {у,х}, {а,х}, {а, у}, {у, х, а}}.

Мощность |В(М)\ булеана от универсумома М равна 2^|M|, т.е. \В(М)\ = 2^\М\.

Диаграммы Венна (Круги Эйлера) Джон Венн (1834-1923) Леонард Эйлер (1707-1783)

М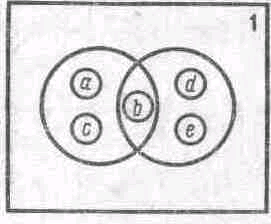ножество также часто задают графически с помощьюдиаграмм Эйлера.

Например, задание множества {{а, b, с}, {b, d, е}} в пространстве 1 = {а, b, с, d, е} приведено на рис. 1.1, где замкнутая линия, называемая кругом Эйлера, соответствует одному из рассматриваемых множеств и ограничивает его элементы, при этом рамка, в верхнем правом углу которой стоит 1, ограничивает элементы пространства. Другие способы задания множеств будут рассмотрены по мере необходимости.

На рис. 1.1 приведены диаграммы Венна, (называемые также иногда кругами Эйлера), иллюстрирующие операции над множествами. Сами исходные множества изображаются фигурами (в данном случае овалами), а результат графически выделяется (в данном случае для выделения использована штриховка).

Ограниченные множества. Границы множеств

Пусть на некотором множестве X задана числовая функция f(х).

Верхней гранью (границей) функции f(х) называется такое число С, что для любого элемента xX С≥f(х).

Нижней гранью (границей) функции f(х) называется такое число d, что для любого элемента xX d≤f(х).

Границы С, d оценивают значение функции f(х) сверху и снизу.

Или пусть X – частично упорядоченное множество. Е – подмножество множества X, то есть .

Элемент являетсяверхней (нижней) границей множества Е, если для любого справедливо неравенствоx ≤ y (x ≥ y). Совокупность всех верхних границ Е будем обозначать Е^s, а всех нижних границ – через Еⁱ. В случае, когда Е^s (Еⁱ) не пусто то, говоря, что Е ограничено сверху (снизу).

Пусть X - частично упорядоченное множество, Е — подмножество множества X.

Элемент есть верхняя {нижняя} граница множества Е, если для любого справедливо неравенство х ≤ у (соответственно, х ≥ у).

Точная верхняя (нижняя) граница

Совокупность всех верхних границ Е обозначается через Е^s, всех нижних границ - через Еⁱ. В случае, когда Е^s (Еⁱ) непусто, говорят, что Е ограничено сверху {снизу). Если элемент z принадлежит пересечению (соответственно, ), то он является наибольшим {наименьшим} элементом множества Е. Выражение типа (Е^s)ⁱ эквивалентно Е^si. Непустота пересечения {} означает, что среди верхних (нижних) границ Е имеется наименьшая (наибольшая); ее называют точной верхней {нижней) границей, или верхней {нижней) гранью множества Е.

Утверждение. Пересечения {} не могут содержать более одного элемента

Доказательство.

Пусть. Тогда х ≤ у, поскольку. Аналогичным образом убеждаемся в справедливости противоположного неравенства y ≤ x А тогда х = у.

Верхняя (нижняя) грань, если она существует, обязательно единственна. Точная верхняя граница (supremum) множества Е обозначается символом sup Е, точная нижняя граница (infimum) — символом inf Е.

Если элементы Е занумерованы с помощью некоторого множества индексов Ξ = {ξ}, то применяются обозначения

sup Е = inf Е =

Если Е состоит из конечного числа элементов х₁, х₂,, ..., х_n, то пишут

sup Е = илиsup Е =

inf Е = или inf Е = .

Основные свойства верхних и нижних границ в произвольном частично упорядоченном множестве X.

1. Если то,.

2. Если и существуют sup Е₁, и sup Е₂ (inf Е₁ и inf Е₂ ), то

sup Е₁ ≤ sup Е₂ inf Е₁ ≥ inf Е₂

3. Соотношения х ≤ у, , равносильны.

4. Пусть E = {Е}—непустой класс подмножеств X, каждое из которых имеет верхнюю {нижнюю) грань. Предположим далее, что совокупность этих граней в свою очередь имеет supremum (соответственно infimum). Тогда этот последний представляет собой верхнюю (нижнюю) грань объединения .

Это свойство называется свойством ассоциативности граней. Его можно выразить формулами

и

предполагая, что фигурирующие в правых частях грани существуют.

Свойства 1-3 очевидны.

Остановимся на доказательстве ассоциативности, ограничившись, случаем верхних граней. Обозначим

,

Для произвольного элемента можно указать множество , которому он принадлежит. Поэтому , Теперь, взяв произвольно, замечаем, что в силу 1 будет для каждого , то есть Видим, что элемент я есть верхняя граница для множества всех , и поэтому . Доказали, что элементy есть наименьшая из верхних границ множества F, то есть точная верхняя граница.

Cвойства, связанные с преобразованием границ при изоморфизмах и дуальных изоморфизмах.

5. Если φ - изоморфизм, то всегда

,

.

6. Если φ - изоморфизм, то всегда

,

.

при условии, что хотя бы одна из граней, фигурирующих в равенстве, существует.

7. Если φ - дуальный изоморфизм, то всегда

,

.

8. Если φ - дуальный изоморфизм то всегда

,

.

с той же оговоркой, что и в 6.

Отметим в заключение очевидную изотонность операций и .

9. Если х₁ ≤ у₁, х₂ ≤ у₂, .... х_n ≤ у_n, то

Принцип двойственности

Пусть К - некоторой класс частично упорядоченных множеств, содержащий вместе с каждым входящим в него частично упорядоченным множеством X также некоторое ему дуально изоморфное. На основании упомянутых свойств 7, 8

7. Если φ - дуальный изоморфизм, то всегда

, .

8. Если φ - дуальный изоморфизм то всегда

, .

можно утверждать, что всякое утверждение, относящееся к свойствам порядка и справедливое для любого , перейдет после замены содержащихся в его формулировке неравенств противоположными, верхних границ нижними, а нижних — верхними в утверждение, также справедливое для всех .

Сформулированный принцип называется общим принципом двойственности для частично упорядоченных множеств.

Точная верхняя (нижняя) граница множества

Если элемент z принадлежит пересечению множества E и множеству всех его верхних границ E^s (соответственно нижних границ Eⁱ), то есть (соответственно), то это элементz является наибольшим (наименьшим) элементом множества E. E^s и Eⁱ также являются множествами и для них можно ввести понятие верхней и нижней границ. Нижняя граница множества верхних границ (E^s)ⁱ обозначается для простоты записи без скобок E^si. Непустота пересечения () означает, что среди верхних (нижних) границE имеется наименьшая (наибольшая). Ее называют точной верхней (нижней) границей, или верхней (нижней) гранью множества E.

Утверждение.

Верхняя (нижняя) грань, если она существует, обязательно единственна.

Доказательство.

Пусть . Тогдаx ≤ y, поскольку ,. Аналогичным образом убеждаемся в справедливости противоположного неравенстваy ≤ x, а это означает, что x = y. Ч.т.д.

Точная верхняя граница (supremum) множества E обозначается символом sup E, точная нижняя граница (infimum) - inf E.

Основные свойства верхних и нижних границ

Пусть X - частично упорядоченное множество.

1. Если , то

,

2. Если и существуютsup E₁ и sup E₂ (inf E₁ и inf E₂), то

sup E₁ ≤ sup E₂

inf E₁ ≥ inf E₂.

3. Соотношения x ≤ y, ,равносильны.

4. Соотношения x ≤ y, ,равносильны.

Множество с атрибутивной точки зрения

Агрегатная точка зрения, в отличие от атрибутивной, является логически несостоятельной в том плане, что она приводит к парадоксам типа Рассела и Кантора (см. ниже).

В рамках атрибутивной точки зрения множества отождествляются со свойством, определяющим соответствующую совокупность элементов. В этом случае записывают m М (сокращенно М (m)) – элемент m обладает свойством М. Здесь m элемент множества М, понимаемого как свойство - оператор отношения предикации,М (эквивалентная запись М( )) является одноместным предикатом (логическим сказуемым, т. е. то, что говориться об элементе m).

Любому св-ву мн-ва М соответствует потенциально бесконечная совокупность элементов, которым присуще это св-во М. В этом плане понятие "конечное мн-во" есть структурно сложные эмпирические или абстрактные объекты (абстрактные агрегаты).

Пример:

1) Учебная группа ИСТАС-2 в рамках атрибутивной точки зрения является структурно сложным эмпирическим (объектом).

2) Абстрактный агрегат {2, 4, 6} является абстрактным структурно сложным элементом составных частей 2, 4, 6, находящихся в отношении четности к числу 2.

3) N = {1, 2, 3, 4…} - множество всех натуральных чисел, т. е. n N (читается "n является натуральным числом")

б) Подход к построению теории множеств может быть содержательным (в читаемом курсе – это алгебраическая система А) и формальным. (Будет рассмотрена в математической логике).

в) В рассматриваемой книге классической теории множеств используется абстракция актуальной бесконечности, мыслимой, в отличие от потенциальной бесконечности, как завершённый объект и к которой применимы все теоретико-множественные операции.

Парадокс Рассела (Бертран Рассел (1872-1970)

Возможность задания множеств характеристическим предикатом зависит от предиката. Использование некоторых предикатов для этой цели может приводить к противоречиям. Например, все рассмотренные в примерах множества не содержат себя в качестве элемента. Рассмотрим множество Y всех множеств, не содержащих себя в качестве элемента:

.

Если множество Y существует, то мы должны иметь возможность ответить на следующий вопрос: ? Пусть , тогда . Пусть , тогда . Получается неустранимое логическое противоречие, которое известно как парадокс Рассела.

Бытовая формулировка парадокса Рассела. В полку имеется полковой Брадобрей, который работает по следующему приказу. Брить бороды только у тех, которые сами себя не бреют. Вопрос может ли Брадобрей брить себе бороду? Ответ: а) если он не бреет себе бороду, то он должен себя брить. Как только он начинает себя брить, то по приказу он не должен себя брить.

Избежать парадоксов удается только в рамках аксиоматической теории множеств, т.е. теории , которая ограничивает способы задания множеств специальной аксиоматикой.

Вот три способа избежать этого конкретного парадокса.

Ограничить используемые характеристические предикаты видом

,

где А — известное, заведомо существующее множество (универсум). Обычно при этом используют обозначение . Для Y универсум не указан, а потому Y множеством не является.

2. Теория типов. Объекты имеют тип 0, множества элементов типа 0 имеют тип 1, множества элементов типа 0 и 1 — тип 2 и т. д. Y не имеет типа и множеством не является.

3. Явный запрет принадлежности множества самому себе: — недопустимый предикат. Соответствующая аксиома называется аксиомой регулярности.

Парадокса Рассела можно избежать, ограничив рассматриваемые множества. Например, достаточно запретить рассматривать в качестве множеств классы, содержащие самих себя. При этом, однако, нет полной уверенности в том, что не обнаружатся другие противоречия. Полноценным выходом из ситуации являлось бы аксиоматическое построение теории множеств и доказательство непротиворечивости построенной формальной теории. Однако исследование парадоксов и непротиворечивости систем аксиом является технически трудной задачей и уводит далеко в сторону от программистской практики, для которой важнейшими являются конечные множества. Поэтому формальная аксиоматика теории множеств здесь не приводится. Мы излагаем необходимые сведения полуформально, опираясь везде, где это возможно, на программистскую интуицию читателя.

Структура

Частично упорядоченное множество X называется структурой, если в нем любое двухэлементное множество имеетточные границы и.

Лемма 1. В любой структуре всякое конечное множество элементов имеет точные границы.

Упражнения

1.Упростить выражение

2. Докажите, что следующие условия эквивалентны 1, 2., 3, 4, 5.

3. Записать множество через пересечение ().

4. Докажите, что . Как называется этот закон?

5. Докажите, что . Как называется этот закон?

1. Группа студентов насчитывает 25 человек. Из них 15 любят математику, 10 — физику, 8 — не любят ни математику, ни физику. Сколько студентов любят и математику, и физику?

2. На собрании студентов-отличников были как студенты второго курса, так и студенты третьего курса. Все они либо любители прозы, либо любители поэзии. Студентов-юношей было 16, а любителей прозы — 24. Студентов-девушек было ровно столько, сколько юношей любителей прозы. Сколько студентов было на собрании?

3. В группе из 100 студентов английским языком владеют 28 человек, немецким — 30, французским — 42, английским и немецким — 8, анг­лийским и французским— 10, немецким и французским— 5, а всеми тремя языками владеют 3 студента. Сколько студентов не знают ни одно­го из названых языков?

Комментарий

ОТСТУПЛЕНИЕ

Существование и анализ парадоксов в теории множеств способствовали развитию так называемого конструктивизма — направления в математике, в рамках которого рассматриваются только такие объекты, для которых известны процедуры (алгоритмы) их порождения. В конструктивной математике исключаются из рассмотрения те понятия и методы классической математики, которые не заданы алгоритмически

Первым и важнейшим математическим пространством является трехмерное эвклидово пространство, предоставляющее собой приближенный абстрактный образ реального пространства. Общее понятие пространства в математике сложилось в результате обобщений и изменений понятий геометрии эвклидова пространства.

В современной математике пространство — это множество объектов, называемых точками, введенными отношениями между точками и теми или иными операциями над элементами множеств.

Примерами пространств могут служить метрическое пространство, нормированное пространство, пространство событий, пространство состояний и целый ряд других пространств. Метрическое пространство — это множество точек Х с расстоянием между ними d>0, удовлетворяющем трем аксиомам:

1) d(х, у) =0 тогда и только тогда, когда х=у (аксиома идентичности);

2) d(х, у) = d(у, х) (аксиома симметрии);

3) d(х, у) = d(х, z) + d(y,z) + d(y,z), где х,у,zХ (аксиома треугольника).

Расстояние d(х, у) называется метрикой, а пара (х, d) — метрическим пространством. Простейшим примером метрического пространства является множество действительных чисел Х с расстоянием между ними d = \х - у\.

В двумерном эвклидовом пространстве Е² (плоскости) расстояние между двумя точками М₁(х₁,y₁), М₂(х₂ ,у₂) определяется по выражению d² = (х₁ – х₂)² + (у₁ – y₂)². Эта же формула распространяется на трехмерное эвклидово пространство d² = (х₁ – х₂)² + (у₁ – y₂)² + (z₁ - z₂)² и на многомерное его обобщение Еⁿ, в котором элементами множества Х являются упорядоченные наборы <х₁, х₂, ..., х_i ..., х_n> действительных чисел: расстояние между двумя точками этого пространства определяется по выражению

d² = (х₁ – х₂)² + (у₁ – y₂)² + (z₁ - z₂)²

Линейные пространства — это такие множества, элементы которых удовлетворяют следующим условиям:

1) для каждой пары элементов х,уХ определен третий элемента zХ, называемый их суммой и обозначаемой как х+у. При этой сумма удовлетворяет следующим условиям: х+у=у+х,

x+(у+v) = (x+у)+v;

2) во множестве Х существует такой элемент 0, что х+0 = х для всех хX;

3) для всех хХ существует такой элемент -х, что х+(-х) = 0;

4) для любого числа а и любого элемента хX определен элемент а такой, что (а+β)х = ах+βx, а(х+у) = ах + ау.

Очевидным примером линейного пространства является множество действительных чисел с обычными правилами их сложениям умножения. Если n-мерном эвклидовом пространстве E* упорядоченные наборы чисел <х₁, ..., х_i, ..., х_n>Х считать координатами векторов с условием, что нулевой вектор – это вектор с нулевыми значениями <х₁, ..., х_i, ..., х_n>, то такое векторное пространство линейное, потому что операции действия с вектором отвечают перечисленным выше аксиомам.

Дальнейшим расширением понятия линейного пространства является линейное нормированное пространство. Это такое пространство, в котором для каждого элемента хX существует неотрицательное число ||х||, называемое его нормой и удовлетворяющее следующим условиям:

||х|| = 0, тогда и только тогда, когда х = 0;

||ах|| = а||х||, где а — некоторое число;

||х+y|| ≤ ||х|| + ||y||

Линейное нормированное пространство является метрическим пространством с нормой d = ||х - y||, так как эта норма удовлетворяет аксиомам метрического пространства:

||х - y|| = 0, если х = у; ||х - y|| = ||y-х||; ||х - y|| ≤ ||х - z|| + ||z - y||

Нормой ||х|| в одномерном векторном пространстве Е¹ является абсолютная величина х. Нормой двумерного пространства (плоскости) Е² является длина вектора, вычисляемая по выражению ||х|| = . Для n-мерного векторного пространства норма ||х|| определяется по аналогии с двухмерным пространством

||х|| = .

В заключение следует сказать, что в терминах линейных векторных пространств формулируются задачи математического программирования, и в частности, дискретного программирования, которое относят к задачам дискретной математики.

Контрольные вопросы и задачи

1. Дайте определение множества.

2. Что такое множество? Как его обозначить? Как можно задать множество? Что такое подмножество?

3. Когда множество считается заданным?

4. Как принято обозначать и задавать множества? Приведите примеры задания множеств.

5. Какое множество называется пустым?

6. Когда множества равны?

7. Равны ли множества А = {а, b, с, d}, В = {а, b, с, d}?

8. Что такое семейство множеств?

9. Из скольких множеств состоит семейство А = {{0}, {1,2}, {1,2},{0}}?

10. Принадлежит ли элемент 2 множеству A={{ 1,2}, {1,2, 3}}?

11. Дайте определение включения множеств.

12. Является ли множество A = {х |0 ≤ х ≤ 1} подмножеством В = {х| 1≤ х≤ 3}, подмножеством С = {х |-3 ≤.х ≤2}?

13. Какое минимальное число подмножеств имеет не пустое множство?

14. Запишите все подмножества множества А = {1, 4}.

15. Перечислите все элементы индексированного множества Z = {zi|1≤i≤3}. Запишите индексное множество.

16. Какие множества называются конечными? Приведите примеры конечных и бесконечных множеств.

17. Выпишите элементы объединения множеств А = {а,b}, В = {1,b}, С = {1,d}.

18. Выпишите элементы пересечения множеств A = {{a,b}, {}, {a}}, B={{с},{a},{1}}.

19. Выпишите элементы множества М = А - В для множеств' .4 ={1,3, 5}, В ={5, 6, 7}.

20. Выпишите элементы множества М = (А - В)(АВ) для множств А = {1, 2, 3, 4, 5}, В = {3, 4, 5}; для множеств А = {2, 4, 5}, B = {1, 4}; для множеств А = {1}, В =.

21. Дайте определение разбиения множества. Приведите все разбиения для множества А = {a, b, с}.

22. Какие множества называются эквивалентными? В каких случаях эквивалентны конечные и бесконечные множества?

23. Дайте определение счетного множества.

24. Что такое мощность множества? Дать определение.

25. Чему в математике служат отношения?

26. Как классифицируются отношения в зависимости от числа связей между элементами множества?

27. Дайте определение бинарного отношения.

28. Что представляет собой декартово произведение множеств?

29. Выпишите декартовы произведения множеств А = {а, b}, В = {1, 3}; декартового квадрата А = {1, а}.

30. Сколько элементов включает декартовый квадрат множества A = {1, 2,...,i, ...,n}?

31. Дайте определение бинарного, тернарного и n-арного отношения в терминах множеств.

32. Что понимают под рефлексивными и антирефлексивными отношениями?

33. Как характеризуются симметричные, асимметричные и антисимметричные отношения?

34. Дайте определение транзитивного отношения.

35. Дайте определение отношения эквивалентности и приведите примеры.

36. Какое отношение называется отношением нестрогого порядка? Является ли отношение ≤ на множестве А = {1, 2, 3} отношением нестрогого порядка?

37. Какое отношение называется отношением строгого порядка?

38. Какое множество называется упорядоченным, полностью упорядоченным?

39. Что такое линейный порядок?

40. Дайте определение функции.

41. Является ли отношение R = {<1,а>, <1,b>, <2,а>}, определенное на декартовом произведении множеств А = {1,2}, B = {а, b}, функцией?

42. Является ли функция f(х) = х2 инъективной?

43. Что представляет собой функционал?

44. Как в математике определяется пространство?

45. Какое пространство называется метрическим?

46. Что представляет собой линейное пространство?

47. Дайте определение линейного нормированного пространства.

Контрольные вопросы

1. Какие основные символы, используемые в теории множеств, вы знаете?

3. Какие основные операции выполняются над множествами?

4. Какое множество можно назвать универсальным?

5. Что такое диаграмма Эйлера-Венна? Проиллюстрируйте с помощью диа­граммы Эйлера-Венна объединение и пересечение трех множеств.

6. Каковы соотношения между множествами и составными высказывани­ями?

7. Сформулируйте и докажите основные тождества алгебры множеств.

8. Что называется кортежем и какие кортежи называются равными?

9. Что такое: декартово произведение множеств; декартова степень некото­рого множества А; бинарное отношение, заданное на множестве А?

10. Назовите основные свойства бинарных отношений. Какое отношение на­зывается рефлексивным, симметричным, антисимметричным, транзитивным? Какое отношение называется отношением эквивалентности?

11. Дайте определение отображения множества А во множество В. Поясните термин «мощность множества».

12. Что такое сюръекция, инъекция, биекция?

Лекция № 3

Подобно тому, как дар слова обогащает нас мнениями других, так язык математических знаков служит средством еще более совершенным, более точным и ясным.

Н. И. Лобачевский