Следствия и равносильности логики предикатов

Равносильности для	Правила	Равносильности для
	Правила перестановки кванторов
	Перенос отрицания с квантора на предикат

Применение предикатов в алгебре

Рассмотрим предикаты, в которых свободной является лишь одна переменная, которую обозначим через х, и обсудим применение предикатов в алгебре.

Типичным примером является уравнение, например, х²-Зх+2=0. Свободная переменная может принимать здесь любое числовое значение. Для некоторых чисел х (а именно х = 1, х = 2) утверждение, содержащееся в этом уравнении, истинно, в остальных оно ложно. В подобных случаях, когда истинность или ложность предиката зависит только от значения, принимаемого свободной переменной х, множество допустимых значений х можно рассматривать как множество логических возможностей U, а множество всех значений этой переменной, при которых высказывание истинно — как его множество истинности.

В приведенном выше примере множество U состоит из всех действительных чисел, а множеством истинности является множество {1,2}.

В результате введения понятия множества истинности для предикатов мы сможем сказать, что решить уравнение — значит найти один элемент или все элементы его множества истинности. При решении системы двух уравнений у нас имеется предикат, представляющий конъюнкцию двух уравнений. Поэтому мы ищем пересечение двух множеств истинности. Если это пересечение пусто, то система уравнений не имеет решений. Такие уравнения называются несовместными, поскольку их множества истинности не имеют общих элементов х.

Понятие множества истинности удобно не только в вопросах, связанных с решением уравнений, но и при рассмотрении неравенств.

Если U — множество действительных чисел, то множество истинности неравенства х < 0 состоит из всех отрицательных действительных чисел. Множество же истинности неравенства х > -3 состоит из всех действительных чисел, больших, чем -3. Если мы потребуем, чтобы эти неравенства выполнялись одновременно, то множеством истинности будет множество, являющееся пересечением двух исходных множеств, т.е. все действительные числа между -3 и 0.

Понятие множества истинности предиката позволяет выяснить, чем разнятся между собой уравнения и тождества. Когда мы решаем уравнение, мы тем самым ищем один из элементов множества истинности этого уравнения или все его элементы. Если же мы доказываем тождество, то тем самым утверждаем, что оно справедливо для всех х. Таким образом, тождество представляет собой уравнение, множеством истинности которого является универсальное множество U, т. е. является логически истинным или тождественно истинным.

Предикаты P и Q, определенные на X, называются равносильными, если P(х₁, х₂, ..., х_п) ≡ Q(х₁, х₂, ..., х_п) для любого набора (х₁, х₂, ..., х_п ) предикатных переменных на X

Пусть P - предикат, определенный на X. Отрицанием предиката P называется предикат, обозначаемый определенный P (неP) на X следующим образом:

P(х₁, х₂, ..., х_п) = P(х₁, х₂, ..., х_п)

Пример. P(х₁, х₂) = P(х₁, х₂) = "Натуральное число х₁ делится (без остатка) на натуральное число х₂". P(4, 2) = 0, P(5, 3) = 1,

Пусть P и Q предикаты, определенные на X.

Дизъюнкцией (конъюнкцией, импликацией, эквиваленцией) предикатов P и Q называется предикат, определенный на X обозначаемый PQ, PQ, PQ, PQ, и определяемый следующим образом:

PQ(х₁, х₂, ..., х_п) ≡ P(х₁, х₂, ..., х_п)Q(х₁, х₂, ..., х_п)

PQ(х₁, х₂, ..., х_п) ≡ P(х₁, х₂, ..., х_п)Q(х₁, х₂, ..., х_п)

PQ(х₁, х₂, ..., х_п) ≡ P(х₁, х₂, ..., х_п)Q(х₁, х₂, ..., х_п)

PQ(х₁, х₂, ..., х_п) ≡ P(х₁, х₂, ..., х_п) Q(х₁, х₂, ..., х_п)

Булева алгебра предикатов

Так как к предикатам можно применять логические операции, то для них справедливы основные законы булевой алгебры.

Теорема. (Свойства логических операций для предикатов).

Множество n-местных предикатов, определенных на X, образуют булеву алгебру предикатов, т.е. для них справедливы основные равносильности булевой алгебры.

1. - закон двойного отрицания

2. - коммутативность дизъюнкции;

3. - коммутативность конъюнкции;

4. - ассоциативность дизъюнкции;

5. - ассоциативность конъюнкции;

6. - дистрибутивность дизъюнкции относительно конъюнкции;

7. - дистрибутивность конъюнкции относительно дизъюнкции;

8. ;- законы де Моргана;

9. ;- идемпотентность;

10. ;;; - законы единицы и нуля

- идемпотентность;

11. ; - закон поглощения

12. ; - закон поглощения

13. -закон исключенного третьего

14. -закон противоречия

Формулы логики предикатов

Наряду с определенными предикатами — для которых истинность или ложность известны для каждого набора значений свободных предметных переменных, будем рассматривать переменные предикаты, для которых не определены значения. Будем обозначать переменные предикаты большими буквами из конца латинского алфавита с приписанными предметными переменными или без них:

W(х₁, х₂, ..., х_п); U(х,у),....

Применяя к переменным предикатам операции ;; →; ↔; Ї; ; , получим формулы логики предикатов,

Формулой логики предикатов называется выражение, составленное из переменных предикатов с помощью логических операций и кванторов и обращающееся в конкретный предикат при подстановке вместо переменных конкретных предикатов.

Пример.

((х)W(х, у)В)→ U(z) — формула логики предикатов. Формула логики предикатов называется тавтологией, если при подстановке любых конкретных предикатов она всегда обращается в тождественно истинный предикат.

Формулы

Определение формулы лежит в основе так называе­мой логики предикатов первого порядка, в которой разрешается квантифицировать (связывать кванторами) только предметные переменные. Логика предикатов первого порядка включает в себя все формулы логики высказываний, все равносильности исчисле­ния высказываний, а также большинство правил вывода умоза­ключений из классической логики. Поэтому язык логики преди­катов дает возможность анализировать рассуждения естественно­го языка и науки, делать выводы в различных формальных системах.

Так, высказывательная форма является форму­лой. В то же время высказывательная форма не будет формулой, поскольку в формуле переменнаях свя­зана квантором существования, тогда как в формуле Q(x) эта же переменная свободна.

В чем ценность формальных теорий?

Для описания каких объектов используется логика предикатов?

Вообще говоря, ценность любой формальной теории заключа­ется в возможности описывать с ее помощью произвольные объек­ты и связи между ними.

Теоремы.

К числу основных равносильностей логики предика­тов относят:

1. .

2. .

3. .

4. .

5. .

6. .

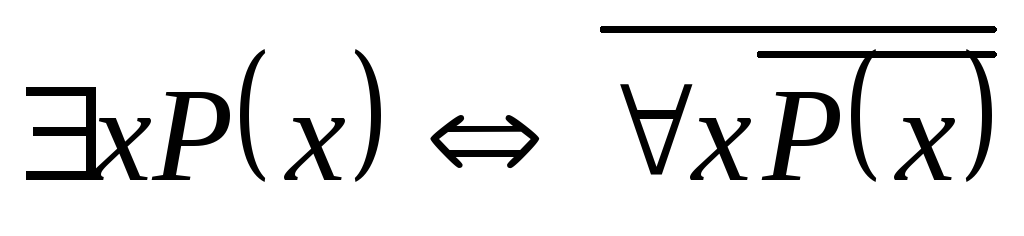Сформулируем следующие правила.

(1) Формула логики предикатов называется атомарной, т.е. элементарной, если в ней нет связанных переменных.

(2) Пусть F — формула, тогда неF — тоже формула. Свободные и связанные переменные формулы неF — это соответственно свободные и связанные переменные формулы F.

(3) Пусть F и G — формулы, причем в них нет предметных переменных, которые были бы связаны в одной формуле и свободны в другой.

Тогда FG, FG, F→G, F↔G — формулы, в которых свободные переменные формул F и G остаются свободными, а связанные — связанными.

(4) Пусть F — формула, содержащая свободную переменную х. Тогда (х)F, (х)F — тоже формулы, в которых переменная х связана, а остальные свободные переменные, входящие в F, остаются свободными.

Заметим, что по определению формулы никакая переменная не может быть одновременно свободной и связанной.

Значение формулы определено лишь тогда, когда задана какая-то интерпретация входящих в нее символов.

Под интерпретацией понимают систему М=<М,f>, состоящую из непустого множества М и соответствия f, которое сопоставляет каждой формуле определенный предикат. При заданной интерпретации предметные переменные пробегают множество М, а логические символы и символы кванторов имеют свой обычный смысл.

Равносильные формулы логики предикатов

Пусть формулы F и G имеют одно и то же множество свободных переменных (в частности, пустое). Формулы F и G равносильны в данной интерпретации, если они принимают одинаковые значения на любом наборе свободных переменных, т. е. выражают в данной интерпретации один и тот же предикат.

Формулы F и G равносильны на множестве М, если они принимают одинаковые значения во всех интерпретациях заданных на множестве М.

Формулы F и G равносильны в логике предикатов, если они равносильны на всех множествах (F = G).

Рассмотрим правила перехода от одних формул к другим, им равносильным.

(1) Перенос квантора через отрицание. Пусть W(х) — формула, содержащая свободную переменную х. Тогда справедливы равносильности:

, ,

, .

(2) Вынос квантора за скобки. Пусть формула W(х) содержит свободную переменную х, а формула В не содержит переменной х. Формулы W(х) и В удовлетворяют третьему правилу создания формул. Тогда справедливы равносильности:

, ,

, .

(3) Перестановка одноименных кванторов. Имеем

, .

(4) Переименование связанных переменных. Заменяя связанную переменную формулы W другой переменной, не входящей в эту формулу, в кванторе и всюду в области действия квантора, получим формулу, равносильную W.

Приведенные и нормальные формы в логике предикатов

Рассмотрим способ упрощения формул, опирающийся на приведенные равносильности.

Формулы, в которых из логических символов имеются только символы конъюнкция, дизъюнкция и отрицание, причем символ отрицания встречается над символами предикатов, будем называть приведенными.

Пример.

Формула (x₁) A₁⁽¹⁾(x₂) (x₁)не(А₂⁽²⁾(x₂,x₃)) — приведенная;

Формула не(x₂) A₁⁽¹⁾(x₂) → А₂⁽¹⁾(x₁) — неприведенная.

Для любой формулы существует равносильная ей приведенная формула, причем множества свободных и связанных переменных этих формул совпадают.

Такая приведенная формула называется приведенной формой данной формулы.

В логике высказываний мы ввели две нормальные формы — дизъюнктивную нормальную форму и конъюнктивную нормальную форму.

В логике предикатов также имеется нормальная форма, цель которой — упрощение процедуры доказательств.

Приведенная формула называется нормальной, если она не содержит символов кванторов или все символы кванторов стоят впереди (т.е. логические символы и символы предикатов стоят в области действия каждого квантора).

Для любой приведенной формулы существует равносильная ей нормальная формула той же длины (под длиной формулы будем понимать общее число входящих в нее символов предикатов, логических символов и символов кванторов).

Нормальная формула называется нормальной формой данной формулы.

Приведем несколько формул, находящихся в нормальной форме:

, ,

.

Алгоритм преобразования формул в нормальную форму

1. Исключить логические связки ↔ и → с помощью формул

F↔G=(F→G)(G→F), F→G=неFG.

2. Использовать закон ненеF=F, законы де Моргана:

не(FG) = неFнеG, не(FG) = неFнеG,

законы

, ,

чтобы пронести знак отрицания внутрь формулы.

3. Переименовать связанные переменные, если это необходимо.

4. Использовать равносильные формулы логики предикатов, чтобы вынести кванторы в самое начало формулы для приведения ее к нормальной форме. Например, приведем формулу к нормальной форме:

Следовательно, нормальная форма формулы — это .

Исчисление предикатов

Исчисление предикатов называют еще теорий первого порядка.

В исчислении предикатов, так же как и в исчислении высказываний, на первом по важности месте стоит проблема разрешимости.

Но в исчислении высказываний проблема разрешимости состояла в решении вопроса является ли данная сложная функция тождественно истинной, выполнимой или тождественно ложной.

Теперь же вопрос следует поставить иначе. Принимает ли данная функция значение 1 при:

а) любых предметных переменных и любых предикатах,

б) на некотором множестве предметных переменных и любых предикатах,

в) при некоторых значениях предметных переменных и любых предикатах,

г) является ли она тождественно ложной, т.е. невыполнимой?

Таким образом, в логике предикатов, в отличие от логики высказываний, нет эффективного способа для распознавания общезначимости функций.

Поэтому в исчислении предикатов указывается некоторая совокупность формул, которые называются аксиомами и составляют аксиоматическую теорию, и указывается конечное множество отношений между формулами, составляющее правила вывода.

Аксиоматическая теория и правила вывода и составляют исчисления предикатов.

Символами исчисления предикатов или алфавитом исчисления предикатов являются символы предметных переменных, символы предикатов, логические символы (отрицание и импликация), символы кванторов, а также скобки и запятая.

Сформулируем аксиомы исчисления предикатов и правила вывода исчисления предикатов.

Аксиомы исчисления предиката.

Пусть A, B и C - любые формулы.

Аксиома 1. A → (B→C).

Аксиома 2. (A → (B→C)) →((A → B) (A→C)).

Аксиома 3. (неB→неA) →((неB → A)→ B).

Аксиома 4. (х_i) A(х_i) → A(х_j), где формула A(х_i) не содержит переменной х_j.

Аксиома 5. A(х_i) → (х_j) A(х_j), где формула A(х_i) не содержит переменной х_j.

Правила вывода исчисления предикатов.

(1) Пусть (А(х) → В) и В не содержит переменной х, тогда

(((x)A(x) → В)

Это правило связывания квантором существования.

(2) Пусть В → А(х) и В не содержит переменной х, тогда

(В → ((x)A(x)))

Это правило связывания квантором общности.

(3) Связанную переменную формулы В можно заменить другой переменной, не являющейся свободной в В. Это правило переименования связанной переменной.

Следование и эквиваленция

Высказывательная форма Q₂ следу­ет из высказывательной формы Q₁, если импликация Q₁→Q₂ об­ращается в истинное высказывание при любых наборах значений переменных, входящих в нее. Для операции логического следова­ния принято обозначение .

Пусть даны предикаты Q₁(x₁, х₂, …, х_n) и Q₂(x₁, х₂, …, х_n), а их множества истинности соответственно T(Q₁) и T(Q₂). Поскольку , то если , т.е. Q₁ истинна, то должна быть истинна Q₂, т.е. . Поскольку такое свойство должно быть у любого элемента из T(Q₁), то это опреде­ление подмножества. Итак, .

Пусть даны два предиката, определенные на одном множестве. Высказывательные формы Q₁ и Q₂ назовем равносильными, если при любом наборе значений переменных, входящих в них, вы­сказывательные формы принимают одинаковые значения истин­ности: . Очевидно, что если ,a то . Тогда T(Q₁) = T(Q₂). т.е. множества истинности равносильных предикатов также совпадают.

Пример.

Пусть высказывательные формы заданы на множестве действительных чисел R.

и х² - 5х + 6 = 0 не являются равносильными.

и Зх + 8 = 0 являются равносильными.

ln (х - 1) + ln (х + 1) = 2 и ln (х² - 1) = 2 не являются равносиль­ными.

их+3 = (х-1)² не являются равносильными.

и (4 - 8х)(2 + х) > 0 не являются равносильными.

и (4 - 8х)(2 + х) > 0 являются равносильными.

и не являются равносильными.

В математике нарушение цепочки тождественных преобразова­ний при решении уравнений или неравенств влечет за собой по­терю имеющихся или приобретение посторонних корней, т.е. из­менение множества истинности исследуемого предиката.

Можно доказать, что отношение равносильности высказывательных форм обладает известными свойствами, а именно, оно рефлективно и симметрично. В том случае, когда одинаковые перемен­ные в каждой из исследуемых форм принимают значения из од­ного множества, отношение равносильности будет обладать также и свойством транзитивности.

Тогда назовем равносильным преобразованием высказывательной формы Q₁ ее замену на равносильную форму Q₂. Две равносиль­ные высказывательные формы с одинаковым набором перемен­ных, для которых установлен одинаковый порядок, определяют один и тот же предикат.

Эти свойства предиката используются при решении уравне­ний и неравенств, которые тоже являются некоторыми высказывательными формами. Так, решение любого уравнения или неравенства предусматривает установление множества его истин­ности, т.е. множества истинности соответствующего ему преди­ката. В процессе поиска множества истинности производят замену одного предиката другим, равносильным данному, с целью упро­щения имеющихся высказывательных форм.

Пример.

2х - 13 + х² - (6х² - 4х + 5 - 6х²) = 0 <=> 6х = 18 <=> х = 3, т. е. множество истинности каждого из этих уравнений состоит из одного числа 3.

Рассмотрим примеры, для которых областью определения яв­ляется множество действительных чисел: D = Е.

Пример.

Для двух высказывательных форм — уравнений (х - 2)(х - 3) = 0 (Q₁) и х - 3 = 0 (Q₂) — из х - 3 = 0 следует, что (х - 2)(х - 3) = 0, т.е. верна запись . Однако из (х- 2)(х- 3) = 0 не следует х - 3 = 0. Например, х = 2 является корнем первого уравнения, но не второго.

Пример.

Из уравнения (х - 5)(х - 2) = 0 следует неравенство х > 0, так как корни уравнения — числа 2 и 5 — удовлетворяют также и неравенству.

Пример.

Тождественно-истинное высказывание х² + 5 > 0 может следо­вать из любой высказывательной формы Q, имеющей непустое множество истинности , т.е. форма Q→ (х² + 5 > 0) истинна при любых значениях х.

Отношения следования и равносильности для высказывательных форм, вообще говоря, зависят от того множества, на котором оно рассматривается.

Пример.

Высказывательная форма х > 9 следует из неравенства 8 < х < 12, если D = {2, 0, 4, 5, 7, 9, 10, 11, 13}, но не следует, если D(Q) = N. Действительно, при D = {2, 0, 4, 5, 7, 9, 10, 11} T(Q₁) = {9, 10, 11}, a T(Q₂) = {9, 10, 11, 13} и выполняется , т.е. форма Q₁ → Q₂ истинна.

Во вто­ром случае (D(Q) = N), T(Q₁) = {8, 9, 10, 11}, a T(Q₂) = {9, 10, 11, 12, 13, 14 ...}, но отношение T(Q₁) с T(Q₂) не выполняется, поскольку .

Правила вывода исчисления предикатов:

Правило заключения (modus ponens) — правило, аналогичное тому, которое введено в исчислении высказываний.

Правило обобщения (-введения, ug-правило) R₂:, где G(x) содержит свободные вхождения х, тогда как F не содержит свободных x.

Правило -введения (eg-правило) R₃:

Нарушение этих требований может привести к ложным выво­дам, полученным из истинных высказываний.

Пример.

Даны предикаты Р(х): «натуральное х делится на 15», Q(x): «х делится на 5». Высказывание Р(х)→Q(x) истинно для любых хN. Приме­ним для него правило обобщения. Имеем Р(х) → x Q(x): «Если х делится на 15, то каждое число х делится на 5». Получили ложное утверждение, так как правило -введения применимо к 0-мест­ным, а не к одноместным, какР(х), предикатам.

Можно доказанные теоремы делать новыми правилами вывода. Так, помимо правил - и-введения можно ввести правила уда­ления кванторов.

Пусть выведена или дана формула xF(x), например «Суще­ствуют студенты, работающие по специальности». Из предметно­го множества всех студентов выберем такого, о котором действи­тельно известно, что он работает по специальности, и для него введем константу а. Поэтому xF(x) → F(a). Это так называемое правило -удаления, или es-правило (правило выбора).

Правило -удаления снимает квантор общности, осуществляя переход от xF(x) к произвольным формулам F(a), F(y) и др. с учетом того, что эти переменные свободны от х в Fx.

Пример.

Из высказывания «Каждый студент колледжа владеет компьюте­ром» будет следовать, что конкретный студент Максимов тоже владеет компьютером, и произвольно выбранный некоторый сту­дент у владеет компьютером, и всякий студент z тоже владеет компьютером. При этом необходимо помнить, что предметные переменные у и z не должны быть связанными.

Правило -удале­ния называют правилом универсальной конкретизации, или us-npaвилом.

Примеры.

1. «Все металлы (М) — плавятся (П). Цинк (Ц) — металл. Зна­чит, цинк плавится». Формализация в логике предикатов примет вид: x(M(x) →П(х)) x(Ц(x)→ М(х))├ x(Ц(x)→ М(х)). Снятие квантора общности: (М(х) → П(х)) (Ц(х) → П(х)); тогда на основании транзитивности импликации имеем (Ц(х) →М(х)), (М(х) → П(х)) ├ Ц(х) → П(х).

Вывод x(Ц(x) →П(х)) — обобщение по R₂ — верен.

2. «Все студенты (С) проходят практику (П). Некоторые студен­ты работают в фирме (Ф), значит, некоторые работающие в фир­ме — проходят практику». Формализация примет вид: x(C(x) → П(х)) х(С(х) Ф(х)) ├ х(Ф(х) П(х)). Уберем кванторы по правилам us и es. Имеем (С (a) → П(а)) (С(a)Ф(а)) (С (а) →П(а))С (а)Ф(a) П(а)Ф(а).

Вывод: х(П(х)Ф(х)), т.е. существуют студенты, которые проходят практику в фирме.

Свойства отношения классификации

Рассмотрим непустое мно­жество U. Пусть дана одноместная высказывательная форма Ф с переменной, которая принимает значения из U, проявляя свой­ство некоторых объектов из него и соответствуя некоторому пре­дикату Q. Множество истинности T(Q) таких объектов является подмножеством U как универсального множества.

Пример.

Пусть дано U_x = {5, 6, 7, 8, 9, 10, 11, 12, 13, 14 ...}.

Высказывательной форме «5 < х < 12» соответствует подмножество

T₁(Q) = {5, 6, 7, 8, 9, 10, 11} (T(Q₁) U₁).

Из множества U₂ = {1, 3, 5, 7, 9, 11, 13, 15} та же высказывательная форма выделяет множество истинности Т₂( Q) = {5, 7, 9, 11},

из U₃ = {5, 6, 7, 8, 9, 10, 11} - T₃ (Q) = U₃,

из U₄ = = {12, 13, 14, 15} рассматриваемая высказывательная форма выде­ляет пустое подмножество истинности T₄(Q) = .

Эта высказывательная форма выражает на множестве U един­ственное свойство, характерное для рассматриваемого предиката на заданном множестве U, т. е. одноместный предикат Q (в дан­ном случае «5 < х < 12») задает свойство данного множества. Тогда множество элементов, обладающих таким свойством Q, будем называть объемом этого свойства.

Если на множестве U задан предикат, выражающий некоторое свойство Р, то множество U можно разбить на два подмножества Т(Р) и U\T(P). Такое разбиение на непере­секающиеся подмножества мы называем классификацией множе­ства U по основанию Р.

Пример.

Так, в предыдущем примере Т(Р) = {5, 6, 7, 8, 9, 10, 11} множество истинности предиката Р: «5 < х < 12» из множества U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15}. U\T(P) = {1, 2, 3, 4, 12, 13, 14, 15}.

Пусть на множестве U задано еще одно свойство Q. Тогда все множество U, разбиваясь на четыре подмножества, представляет новую классификацию. С помощью логических операций такую классификацию записывают в виде: .

Замечание. Это аналогично разложению булевой функции по двум переменным (см. подразд. 4.7), с той разницей, что каждое слагаемое должно иметь вид , так как мы разлагаем формулу исчисления предикатов, имеющую вид тавтологии.

Пример.

Так, в предыдущем примере Т(Р) = {5, 6, 7, 8, 9, 10, 11} множество истинности предиката Р: «5 < х < 12» из множества U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15}. U\T(P) = {1, 2, 3, 4, 12, 13, 14, 15}.

Пусть в нашем примере предикат Q выражает новое свойство — «быть нечетным числом». Тогда эти два свойства одновременно классифицируют множество U на подмножества:

Т(Р)T(Q) = {5, 7, 9, 11}, выполнено Р(х)∙Q(x);

= {6, 8, 10}, выполнено ;

= {1, 3, 13, 15}, выполнено ,

= {2, 4, 12, 14}, выполнено .

Уточним понятие «отношение» с помощью понятия «преди­кат». Во всех n-местных предикатах (n > 2) устанавливаются неко­торые отношения между переменными.

Примеры.

1. Высказывательная форма «х — друг у» выделяет из всего мно­жества людей пары х и у, которые связаны между собой отноше­нием дружбы.

2. Высказывательная форма «х ┴ у» выделяет из множества пар прямых, например на плоскости, те пары, которые связаны от­ношением перпендикулярности.

3. Высказывательная форма «х² + у² + z² = 16» выделяет из всего множества троек координат те, которые связаны отношением «точ­ка с координатами (х; у; z) лежит на сфере с центром в начале координат и радиусом R = 4».

Отрицания в исчислении предикатов

В разговорной речи для построения отрицания обычно перед сказуемым ставят частицу не.

Пример,

1а «Студент х учится на факультете программирова­ния» имеет отрицание

16 «Студент х не учится на факультете про­граммирования».

? Но всегда ли построенное таким образом отрицание истинно?

Утверждения 2а «Все выпускники колледжей продолжили об­разование в вузе» и 2б «Все выпускники колледжей не продолжи­ли образование в вузе» не являются отрицанием друг друга, так как они оба ложны.

Пары утверждений За «Некоторые выпускники колледжей про­должили образование в вузе» и 36 «Некоторые выпускники кол­леджей не продолжили образование в вузе» тоже не служат отри­цанием друг друга, так как они оба истинны.

Вторая и третья пары утверждений отличаются от первых тем, что содержат кванторные слова «все» и «некоторые». А при пост­роении отрицаний для предложений, содержащих кванторы, прием введения отрицания не перед сказуемым не срабатывает.

Можно воспользоваться другим, универсальным, приемом построения отрицаний предложений, содержащих кванторы, добавив общее отрицание неверно, что... Тогда во втором примере «Неверно, что все выпускники колледжей продолжили образование в вузе» со­впадает по смыслу с утверждением «Некоторые выпускники кол­леджей не продолжили образование в вузе». Таким образом, отри­цанием предложения 2а служит 36, а отрицанием За служит 26.

Символически общее отрицание принято записывать с помо­щью либо общей черты, либо отрицания самого квантора.

Для отрицания предложения_возможны записи, или, или:;

для отрица­ния аналогично:, или,

или :.

Эти равносильности являются обоснованием метода по­строения отрицаний высказываний, содержащих кванторы. Для построения отрицания высказываний, содержащих квантор , достаточно заменить его на другой квантор и взять отрицание выражения, на которое этот квантор был «навешен».

Для многоместных кванторов также применяется это правило: осуществляется последовательный перенос отрицания с кванторного слова на предложение, стоящее за квантором, а сам квантор заменяют на двойственный.

Например, для формулы построим отрицание:. В подразд. 4.8 была показана булева двойственность конъюнкции и дизъюнкции. Поэтому для сложных высказываний, состоящих из простых, раз­деленных операциями конъюнкции и дизъюнкции,отрицание стро­ится следующим образом: нужно все кванторы заменить на , и наоборот; все связки и ()заменить на или (),и наоборот; и взять отрицание утверждения.

Контрольные вопросы

1. Что называется предикатом? Приведите примеры предикатов.

2. Какой предикат называется разрешимым, тождественно истинным. Тождественно ложным?

3. Перечислите операции, которые можно осуществить над предикатами. Как применяются предикаты в алгебре? Что такое множество истинности предиката?

4. Из чего состоит алфавит логики предикатов? Что такое квантор?

5. Что называется формулой логики предикатов?

6. Сформулируйте основные правила построения формул.

7. В чем состоит смысл термина «интерпретация» в логике предикатов?

8. Сформулируйте основные правила перехода к новым равносильным формулам.

9. Какая формула называется непротиворечивой, противоречивой, общезначимой?

10. Какая формула называется приведенной? Что такое приведенная форма?

11. Какая формула называется нормальной формой? Сформулируйте алгоритм приведения формулы к нормальной форме.

12. Что называют исчислением предикатов?

13. Сформулируйте аксиомы исчисления предикатов.

Литература

1. Акритас А. Основы комбинаторной алгебры с приложениями. – М.: Мир, 1994

2. Александров П.С. Введение в теорию множеств и общую топологию. М.: Наука, 1977. - 367 с.

3. Архангельский А.А. Канторовская теория множеств. М.: Изд-во Моск. ун-та, 1988, 112 с

4. Аляев Ю.А., Тюрин С.Ф. дискретная математика и математическая логика. - М.: Финансы и статистика, 2006. - 368 с.

5. Асанов М.О., Баранский В.А., Расин .В. Дискретная математика: графы, матроиды, алгоритмы. - Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001.

6. Ахо А., Ульман Дж. Теория синтаксического анализа, перевода и компиляции. М.: Мир, 1978 - с.

7. Ахо А., Хопкрофт Дж., Ульман Дж. Построение и анализ вычислительных алгоритмов. М.: мир, 1979. - с.

8. Басакер Р., Саати Т. Конечные графы и сети. – М.: Наука, 1974.

9. Бауэр Ф.Л., Гооз Г. Информатика. М.: Мир, 1990

10. Белешко Дмитрий ИНТЕРНЕТ

11. Белов В.В., Воробьев Е.М., Шаталов В.Е. Теория графов. – М.: Высш. Школа, 1976

12. Белоусов А.И., Ткачев С.Б. Дискретная математика. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2006. – 744 с.

13. Берж К. Теория графов и ее применение. Изд. Иностр. Лит., 1962

14. Бочаров В.А. Основы логики. М.: Логос, 1994. -296 с.

15. Владимиров Д.А. Булевы алгебры. М.: Наука, 1989. - 318 с.

16. Гаврилов С.П. Сапоженко А.А. Сборник задач по дискретной математике. – М.: Наука, 1978.

17. Гаврилов С.П. Сапоженко А.А. Задачи и упражнения по дискретной математике. – М.: Физматлит, 2006. – 416 с.

18. Галушкина Ю.И. Марьямов А.Н. Конспект лекций по дискретной математике с упражнений и контрольными работами. М.: Айрис ПРЕСС, 2007 – 175 с.

19. Ганчев И., Чимев К., Стоянов Й. Математический фольклор. М.: Знание, 1987.

20. Гиндикин С. Г. Алгебра логики в задачах. М.: Наука; 1972.

21. Горбатов В. А. Фундаментальные основы дискретной математики. М.: Наука; Физматлит, 2000.

22. Горбатов В.А. Основы дискретной математики. М.: Высшая школа, 1986. - 311 с.

23. Гэри М., Джонсон Д. Вычислительные машины и труднорешаемые задачи. М.: Мир, 1982

24. Деньдобренко Б. Н., Малика А.С. Автоматизация конструирования РЭА, М.: Высш. школа, 1980

25. Дискретная математика и математические вопросы кибернетики. Под ред. С.В. Яблонского и О. Б. Лупанова, Наука, 1974

26. Евстигнеев В.А. Применение теории графов в программировании. М.: Наука, 1985 – 352 с.

27. Емеличев В.А., Мельников О.И, Сарванов В.И., Тышкевич Р.И. Лекции по теории графов, М.: Наука, 1990

28. Ерусалимский Я. М. Дискретная математика. М.: Вузовская книга, 2005.

29. Ершов А. П. Введение в теоретическое программирование. М.: Наука, 1977

30. Ершов Д.Л., Палютин Е.А. "Математическая логика". - Спб.: Лань, 2004.

31. А.А. Зыков "Основы теории графов", М, Наука, 1987г.

32. Иванов Б.Н. Дискретная математика. Алгоритмы и программы. Полный курс. - М.: ФИЗМАТЛИТ, 2007. – 408 с.

33. Ивин А.А. Строгий мир логики. – М.: Педагогика, 1988. – 154 с.

34. Капитонова Ю.В., Кривой С.Л. и др. Лекции по дискретной математике. - СПб.: БХВ-Петербург, 2004. – 624 с.

35. Канцедал С.А. Дискретная математика.- М.: ИД «ФОРУМ» - ИФРА-М. 2007.

36. Каргаполов М. И., Мерзляков Ю. И. Основы теории групп. М.: Наука, 1977. - 239 с.

37. Карпов Ю.Г. Теория автоматов, Питер, 2002

38. Клашанов Ф.К. Дискретная математика, часть 1. Основы теории множеств и комбинаторика: Учебное пособие – М.: Изд-во МГСУ, 2010.

39. Кнут Д. Искусство программирования для ЭВМ Основные алгоритмы. Т.1, Мир, 1977

40. Кнут Д. Искусство программирования для ЭВМ Получисленные алгоритмы. Т.2, Мир, 1977

41. Кнут Д. Искусство программирования для ЭВМ Сортировка и поиск. Т.3, Мир, 1977

42. Козлова Е.Г. Сказки и подсказки. – М.: Мирос, 1994.

43. Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ. — М.: МЦНМО, 2001.

44. Кристофидес Н. Теория графов. Алгоритмический подход. М.: Мир, 1978. – 432 с.

45. Кон П. Универсальная алгебра, Мир, 1968

46. Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ. — М.: МЦНМО, 2001.

47. Кузнецов О. П. Дискретная математика для инженеров. М., 2005.

48. Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инженера. – М.: Энергоатомиздат, 1988.

49. Кук Д., Бейз Г. Компьютерная математика. – М.: Наука, 1990.

50. Курейчик В.М. Математическое обеспечение конструкторского и технологического проектирования с применением САПР. – Радио и связь, 1990.

51. Лавров С.С., Гончарова Л.И. Автоматическая обработка данных, хранение информации в памяти ЭВМ, Наука 1988

52. Лавров И.А., Максимова Л. Л. Задачи по теории множеств, математической логике и теории алгоритмов. – М.: Наука 1984

53. Лекции по теории графов/ В. А. Емеличев, О.И. Мельников, В.И. Сарванов, Р. И. Тышкевич. – М.: Наука, 1990

54. Липский В. Комбинаторика для программистов. М.: Мир, 1988 – 213 с.

55. Логический подход к искусственному интеллекту /А. Тейз, П. Грибоман, Ж. Луи и др. – М.: Мир, 1990

56. Макоха А.Н., Сахнюк П.А., Червяков Н.И. Дискретная математика: Учебное пособие. – М.: ФИЗМАТЛИТ, 2005. – 368 с.

57. Мендольсон Э. Введение в математическую логику, Наука, 1984

58. Нечаев В.И. Элементы криптографии. Основы теории защиты информации, Высшая школа, 1999

59. Нефёдов В.Н., Осипова В.А. Курс дискретной математики М.: Изд-во МАИ, 1992.

60. Новиков Ф.А. Дискретная математика для программистов 2-е изд. – Спб.: Питер, 2004. – 364 с.

61. Общая алгебра. Т. 1,2/ О.В. Мельников, В.Н. Ремесленников, В.А. Романьков и др. М.: Наука, 1990.

62. Оре О. Теория графов. - М.: Наука, 1980.

63. Пойа Д. Математика и правдоподобные рассуждения. –м,6 Наука, 1975.

64. Райзер Г.Дж. Комбинаторная математика. М.: Мир, 1966 – 154 с.

65. Расёва Е., Сикорский Р. Математика метаматематики. М.: Наука, 1972. - 591 с.

66. Редькин Н.П. Дискретная математика: Курс лекций для студентов-механиков : учебное пособие. – Спб.: Издательство «Лань», 2006. - 96 с.

67. Рейнгольд Э., Нивергельт Ю., Део Н. Комбинаторные алгоритмы: теория и практика. -М.:Мир, 1980.

68. Романовский И. В. Дискретный анализ. СПб.—М., 2000.

69. Сачков В.Н. Введение в комбинаторные методы дискретной математики. Наука, 1977

70. Сачков В.Н. Введение в комбинаторные методы дискретной математики. Наука, 1982

71. В.Н. Сачков "Введение в комбинаторные методы дискретной математики", М, Наука, Электронная версия лекций Маркина П.М. по курсу "Дискретная математика" – На кафедральном сервере или в интернете.

72. Свами М., Тхуласираман К. Графы, сети и алгоритмы. – М.: Мир, 1984.

73. Спирина М.С. Дискретная математика : для студ. Учреждений сред. Проф. Образования/ М.С. Спирина, П.А. Спирин.- 4-е изд., испр. – М.: Издательский центр «Академия», 2007 г. – 368 с.

74. Соболева Т.С., Чечкин А.В. Дискретная математика: учебник для студ. вузов. – М.: Издательский центр «Академия», 2006. – 256 с.

75. Столл Р. Множества. Логика. Аксиоматические теории. – М.: Просвещение, 1968.

76. Судоплатов С.В., Овчинникова Е.В. Элементы дискретной математики. М.-Новосибирск: ИНФРД-М НГТУ, 2007.

77. Тей А. Логический подход к искусственному интеллекту/А.Тей, П. Грибомон. – М.: Мир, 1990.- 432 с.

78. Шапорев С. Д. Математическая логика. Курс лекций и практических занятий. СПб.: БХВ-Петербург, 2005.

79. Уилсон Р. Введение в теорию графов. Мир, 1977

80. Фрейденталь Х. Язык логики. –М.: Наука, 1969.

81. Фрид Э. Элементарное введение в абстрактную алгебру, Мир. 1979

82. Фридман М., Менон П. Теория и проектирование переключательных схем. – М.: Мир. 1978

83. Фудзисава Т., Касами Т. Математика для радиоинженеров. – М.: Радио и связь. 1984

84. Харари Ф. Теория графов. – М.: КомКнига, 2006. -296 с.

85. Холл М. Комбинаторика. – М.: Мир, 1970

86. Чень Ч., Ли Р., Математическая логика и автоматическое доказательство теорем. Наука, 1983

87. Шенфилд Дж., Математическая логика. – М.: Наука, 1975

88. Эрдниев М.П., Эрдниев Б.П. Укрупнение дидактических единиц как новая технология обучения математике. – М.: Просвящение, 1986.

89. Яблонский С.В. Введение в дискретную математику. М.: Высшая школа, 2003. - 384 с.

90. Ярцев Борис Интернет

91. http://catalog.unior.ru/resinfo.phtm?Res1D=474

92. http://abs.vvsu.ru/Books/Diskr_za/default.asp

93. http://mirea.boom.ru/diskret.htm1

94. http://www.mail.ru/k805/htm1/diskra.htm

95. http://rk-cmb.chat.ru/algo/ln_dm_01.htm

96. http://ulstu.ru/people/SOSNIN/umk/Basis_of_Artificial_Intelligence/m_lect.htm

97. http://www.auditorium.ru/books/339/philosophy/chap06.htm1#i06

98. http://www.isu.ru/slava/do/disc/curshome.htm

99. Harary F. Graph Theory. Reading, MA, Addison-Wesley, 1969 [Русский перевод Харари Ф. Теория графов. М.: Мир, 1973]

100. Oxley J. What is a matroid

101. Post E.L. The two-valued interactive systems of mathematical logic. – Annals of Math. Studies, v. 5, Princeton Univ. Press. Princeton-London, 1941).

ПРИЛОЖЕНИЕ

Буквы латинского алфавита

Представлен наиболее употребительный (но не единствен­ный) вариант произношения (в частности, вместо „йот" иногда говорят „жи").

Наряду с указанным произношением также говорят „лямб­да", „мю"и „ню".

Принятые обозначения

Символы «порядка не более». При сравнении скорости роста двух функций f(n) и g(n) (с неотрицательными значениями) очень удобны следующие обозначения:

f(n) = О(g(п)) существуют константы С, N > 0, такие, что f(n) Сg(п) для всех п N;

f(n) = О(g(п)) <=> существуют константы С, N > 0, такие, что f(n) Сg(п) для любого п N.

Конечно, f(n) = о(g(п)) тогда и только тогда, когда g(п) = О(f(n)). Символы О(g(п)) и о(g(п)) читаются соответственно: «порядка не более чем g(п)» и «порядка не менее чем g(п)».

При изучении курса потребуется следующая символика теоретико-множественных операций и отношений: ,, \,,,,,(Л),card M< смысловое содержание которой приведено в таблице.

(Л)	пустое множество	M=
,	знак включения подмножества	;
;		;
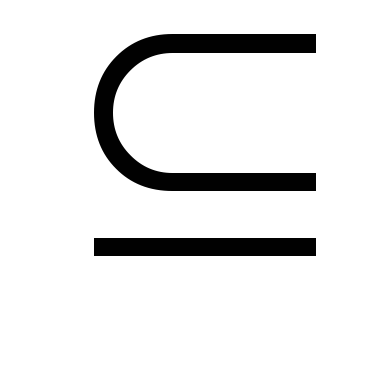	не включение подмножества в множество
│M│, (card M)	Мощность множества

По мере необходимости будут вводиться другие символы, смысл которых будет объясняться при их введении.

Индивидуальные символы для обозначения правил сопоставления 2^x множеств. Индивидуальными (именными) знаками отношений являются символы: , , , , =, , , , <, >, ≤, >которые означают:

- символ принадлежности элемента множеству;

 - символ не принадлежности элемента множеству;

 () - символ строгого включения (не включения) подмножества во множество;

= () - символ равносильности (не равносильности) множеств (языковых выражений);

() - символ нестрогого включения (не включения) одного множества в другое;

<, >, ≤, >; - символ отношений строго меньше, строго больше, меньше и больше.