Пример 1. Исследовать сходимость степенного ряда

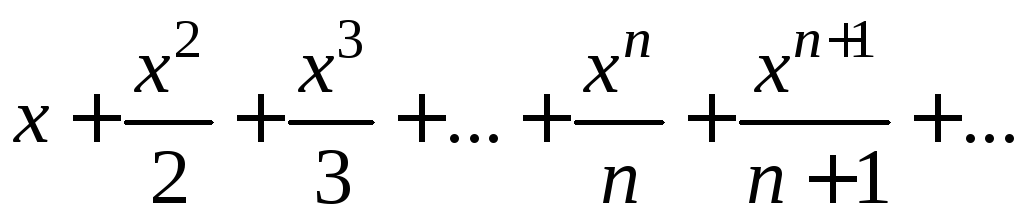
Решение

Здесь Найдем радиус сходимости ряда:

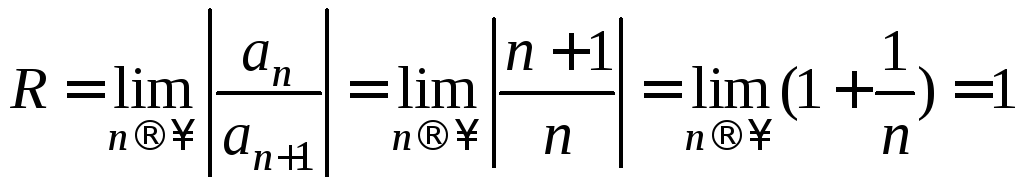
Следовательно, ряд сходится для значений х, удовлетворяющих неравенству х<1 или -1<х<1.

Исследуем сходимость ряда на концах промежутка. Подставляя в данный ряд вместо х число 1, получим гармонический ряд , который, как известно, расходится.

Если х=-1, получаем числовой знакочередующийся ряд 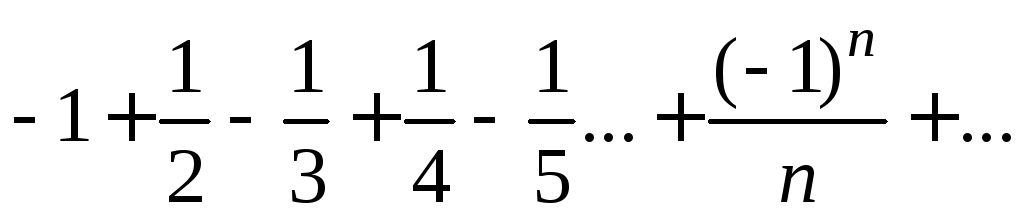Этот ряд сходится, так как удовлетворяет условиям признака Лейбница:

1) ; 2).

Таким образом, данный ряд сходится при всех значениях х, удовлетворяющих неравенствам -1х<1, и его промежуток сходимости представляет собой полузамкнутый интервал [-1;1).

Геометрически это выглядит так:

Пример 2. Найти область сходимости ряда:

Решение. Найдем радиус сходимости этого ряда по формуле .

;

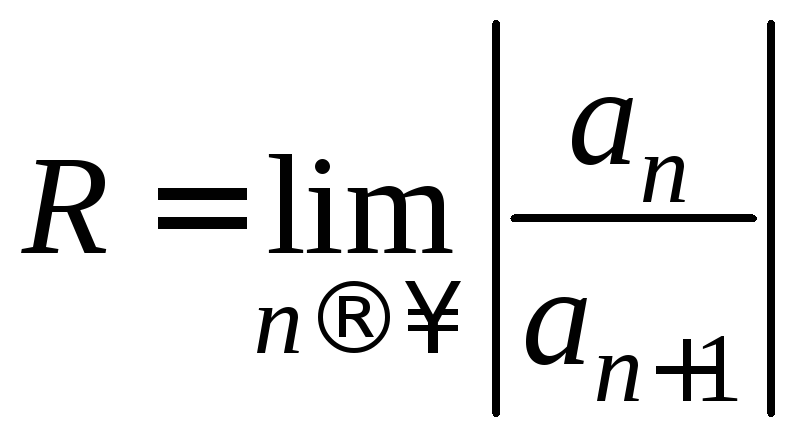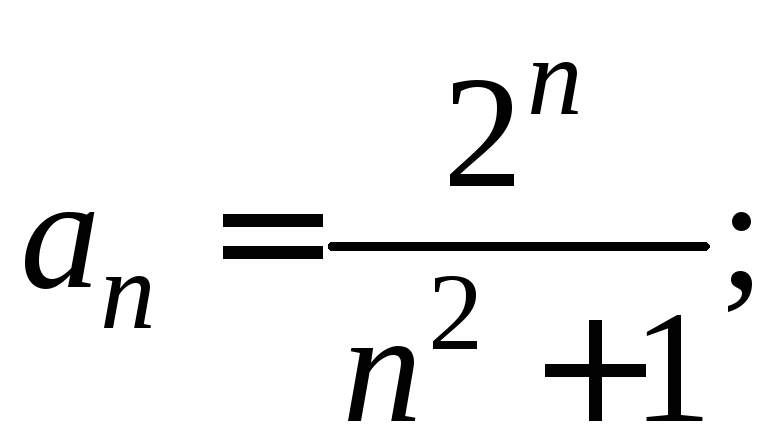
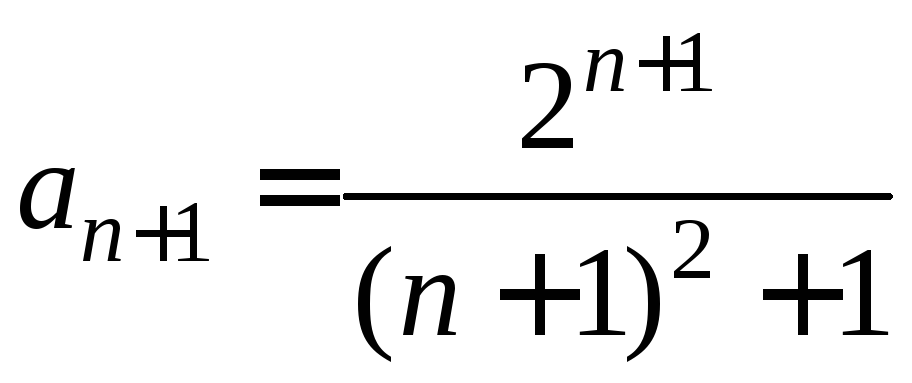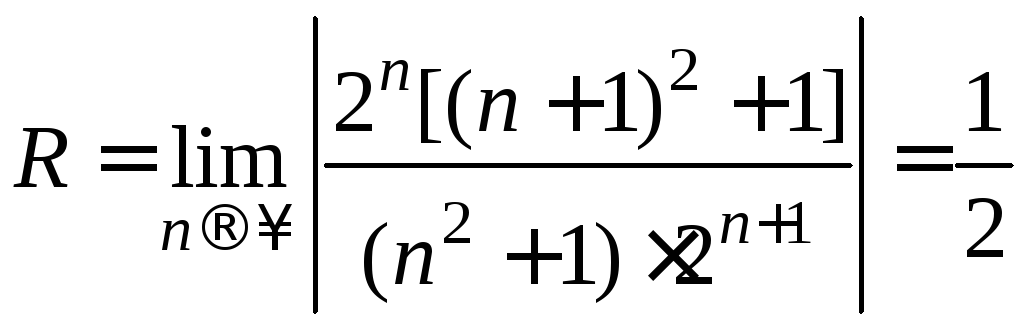
Следовательно, радиус сходимости , а интервал сходимости (-;). Геометрически это выглядит так:

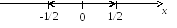
Теперь выясним поведение ряда на концах интервала сходимости. В правом конце, при х=, данный степенной ряд превращается в числовой ряд вида:

Выше сходимость этого ряда была доказана при помощи интегрального признака.

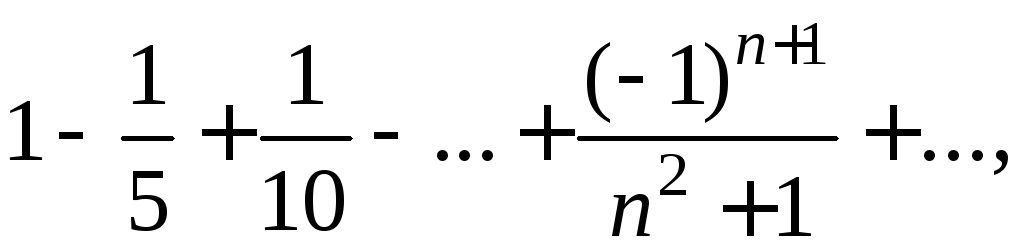В левом конце, при х=-, данный степенной ряд превращается в знакочередующийся рядкоторый сходится абсолютно, так как сходится соответствующий ряд из абсолютных величин:.

Таким образом, данный степенной ряд сходится в обоих концах интервала сходимости, значит, областью сходимости будет отрезок 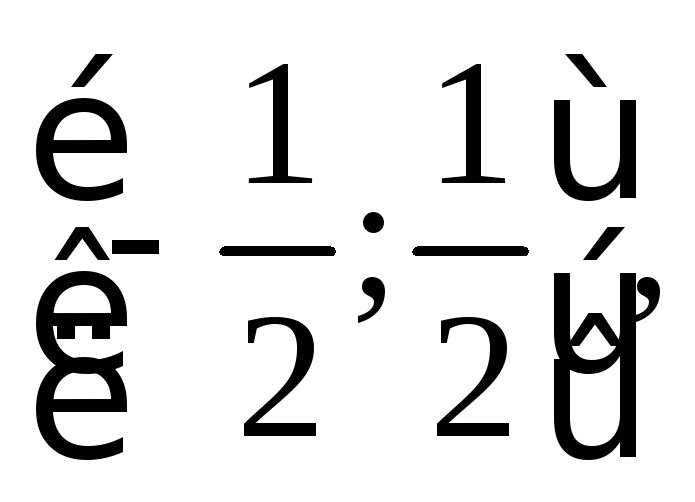т.е..

Графически:

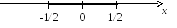
Пример 3. Найти промежуток сходимости ряда:

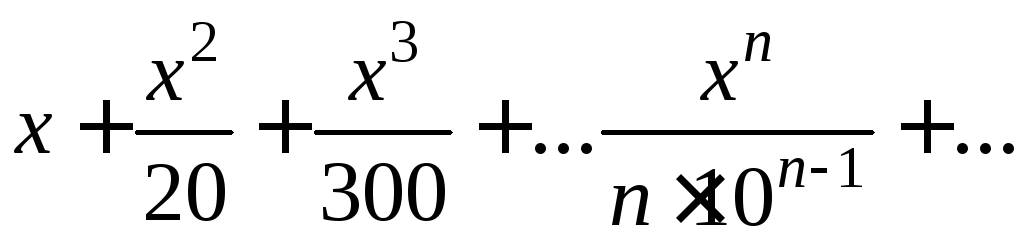
Решение.

Радиус сходимости ряда находим по формуле .

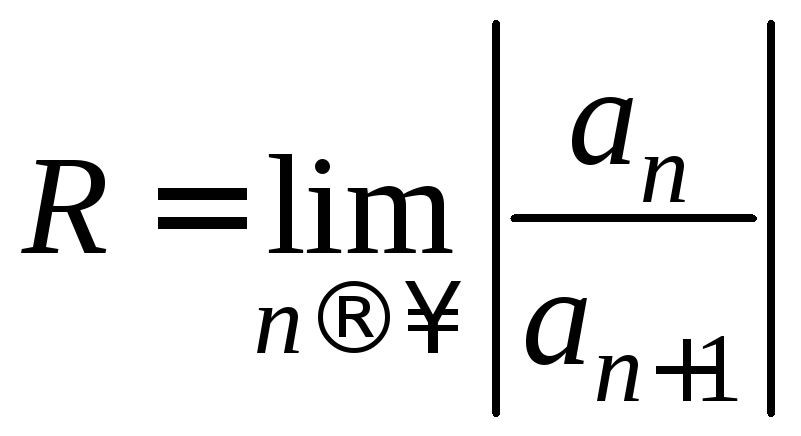В нашей задаче

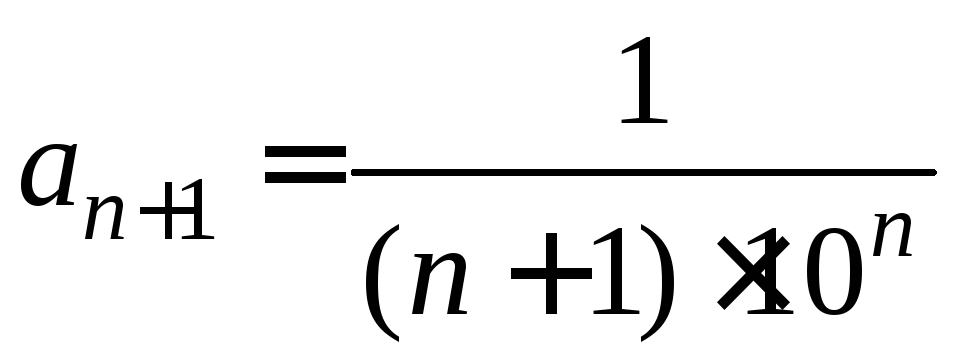
Поэтому .

Значит, данный ряд сходится при значениях х, удовлетворяющих неравенству х<10 или -10<х<10.

Исследуем теперь поведение ряда на концах промежутка. Подставляя в данный ряд вместо х число 10 получаем ряд:

,

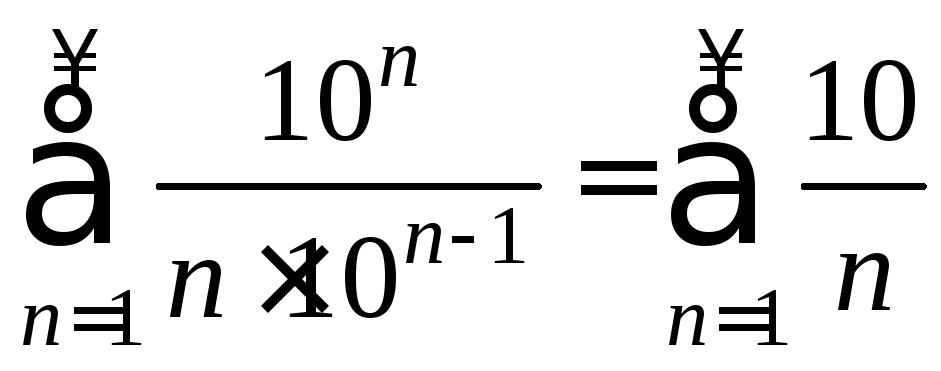который расходится как гармонический (отличаясь от него лишь постоянным множителем)

При х=-10 получим числовой знакочередующийся ряд:

, который сходится условно.

Таким образом, данный степенной ряд сходится при всех значениях х, удовлетворяющих неравенствам -10х<10, и его промежуток сходимости представляет собой полузамкнутый интервал [-10;10).

Графически:

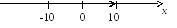
Пример 4. Найти радиус и интервал сходимости степенного ряда

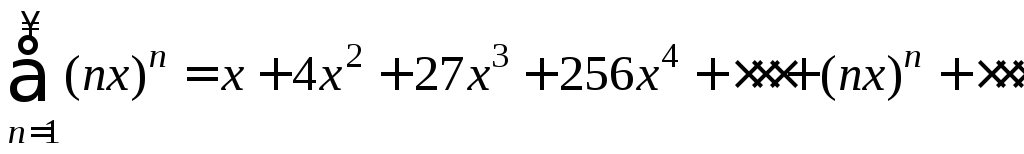
Решение.

;

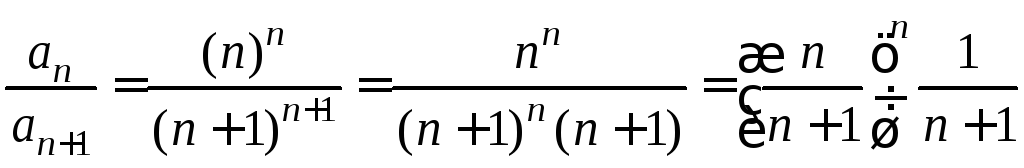Радиус сходимости ряда равен нулю. Ряд сходится в единственной точке х=0

Замечание.

1. При вычислении предела использовали второй замечательный предел .

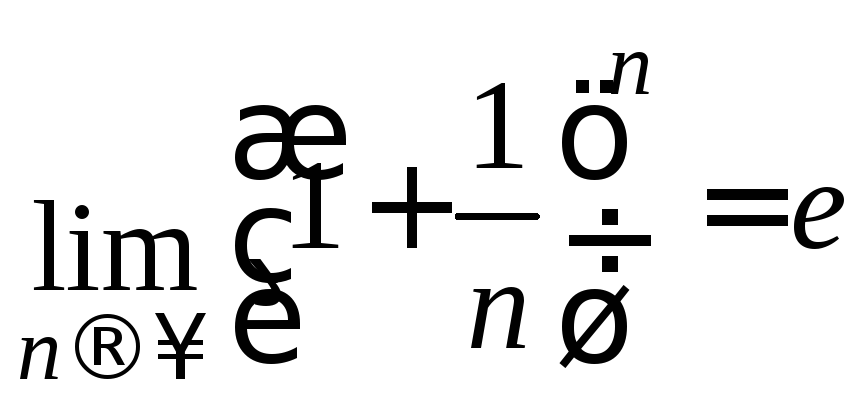2. Тот же результат можно получить и по формуле :

.

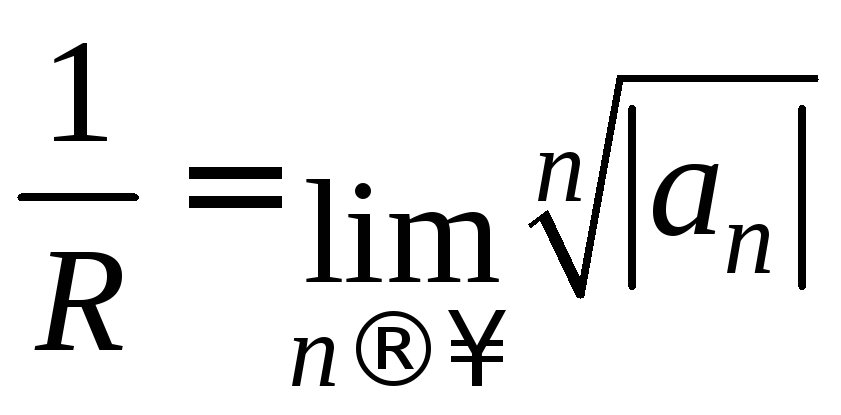Пример 5. Найти радиус и интервал сходимости степенного ряда . Решение

Так как ,

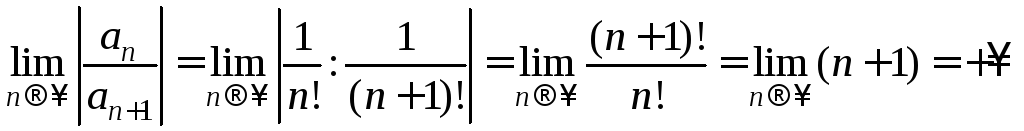то . Ряд сходится при всехх, т.е. в интервале (-; +).

Пример 6. Найти промежуток сходимости ряда

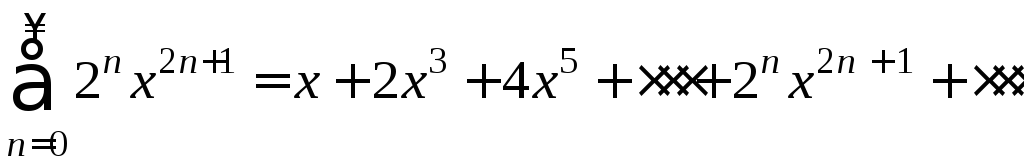
Решение.

Здесь мы не вправе применять формулу 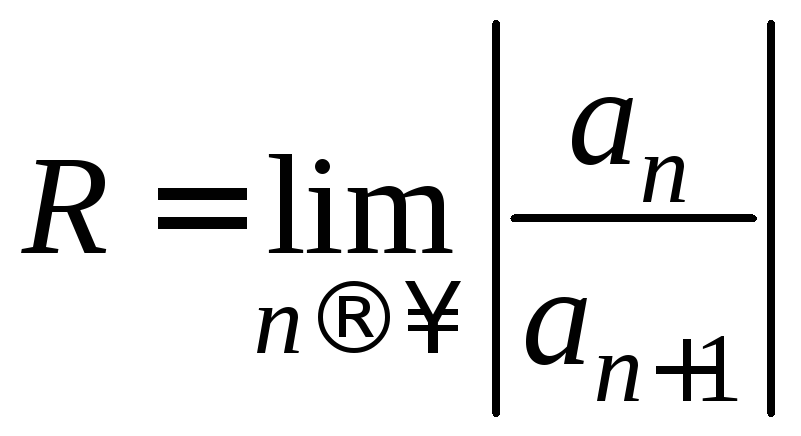для отыскания радиуса сходимости ряда, так как он не содержит четных степенейх. Поэтому промежуток сходимости ряда найдем, воспользовавшись признаком Даламбера.

Данный ряд будет сходиться при всех значениях х, удовлетворяющих

неравенству

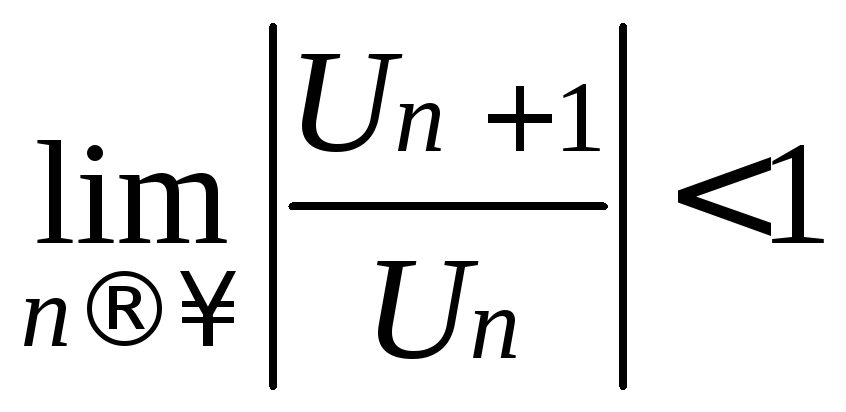т.е. .

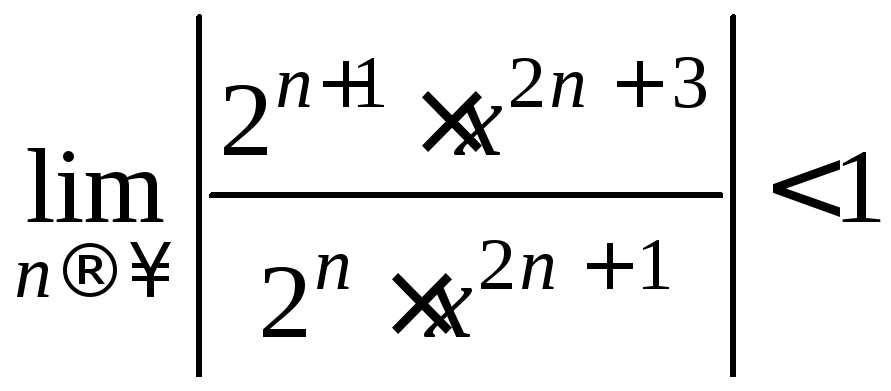Отсюда получаем .

Выражение в скобках не зависит от n, поэтому 2х²<1, или х²<1/2. Окончательно получаем 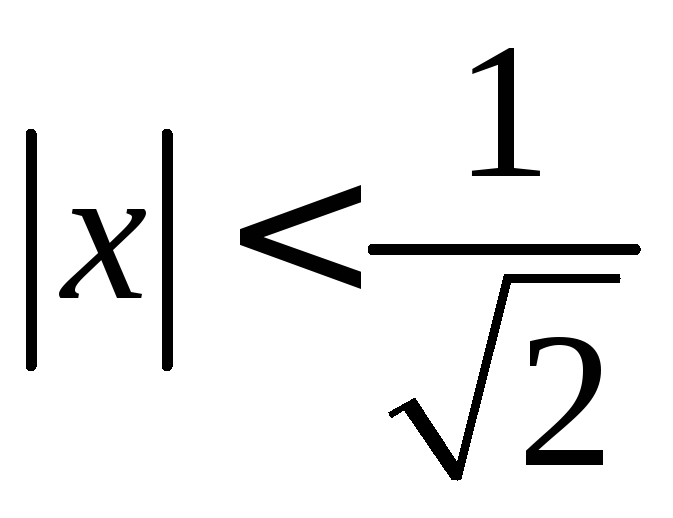, т.е..

Исследуем поведение ряда на концах промежутка.

При получим расходящийся числовой ряд 1+1+1+1+…+1+…

Таким образом, на концах интервала данный ряд расходится. Промежутком сходимости является интервал .

Замечание. Тот же результат можно было получить, воспользовавшись радикальным признаком Коши.

Пример 7 Найти область сходимости степенного ряда

.

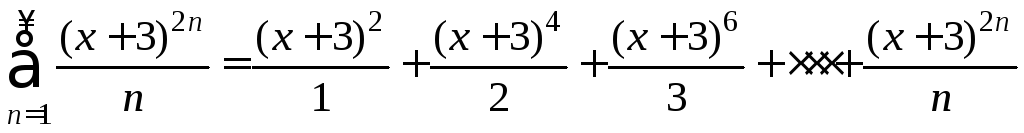Решение: Применим признак Даламбера.

В данном случае .

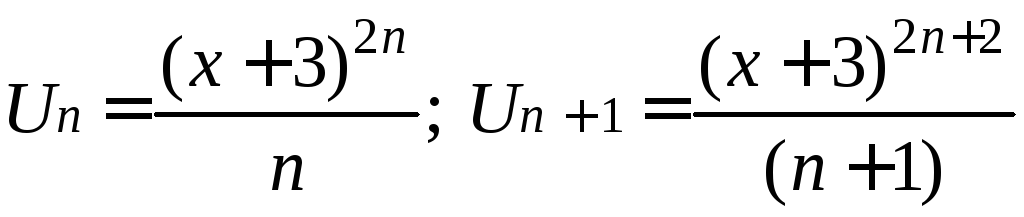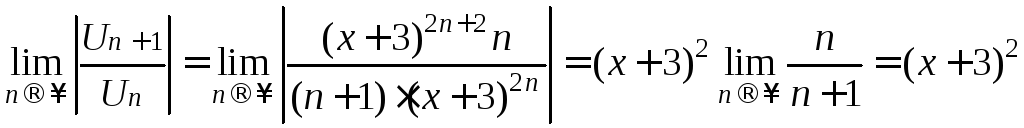
Ряд сходится при (х+3)²<1, т.е. х+3<1, -1<х+3<1, т.е. -4<х<-2.

Исследуем сходимость ряда на концах промежутка (-4; -2). При х=-4 получаем ряд - гармонический ряд, который расходится. Прих=-2 также получаем расходящийся гармонический ряд

Следовательно, областью сходимости данного ряда является интервал

(-4; -2).

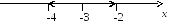
Замечание. В некоторых случаях функциональный ряд можно при помощи замены переменой привести к виду степенного ряда, для нахождения области сходимости которого можно воспользоваться формулами радиуса сходимости.