Лекция No.5.ССКРК

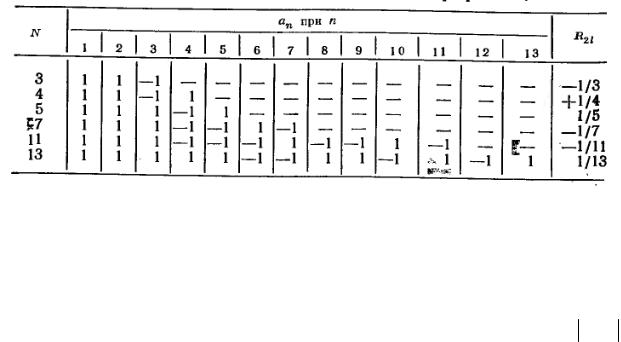
Лекция № 5.

ТЕМА 2. КОДОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И ИХ ОСНОВНЫЕ СВОЙСТВА (продолжение).

где l = 0,1,..., ( N −1) / 2 .

Знак в последней строке (2.1) зависит от величины N.

В табл. 2.2.1 приведены известные кодовые последовательности Баркера. В последнем столбце таблицы приведен уровень боковых пиков автокорреляционной функции (1). Для некоторых N существует две последовательности. Например, для n = 3 имеем {1, –1, 1}, {1, 1, –1}, для N

= 4 – {1, 1, 1, –1}, {1, 1, –1, 1}.

Таблица 2.2.1. Кодовые последовательности Баркера и АКФ

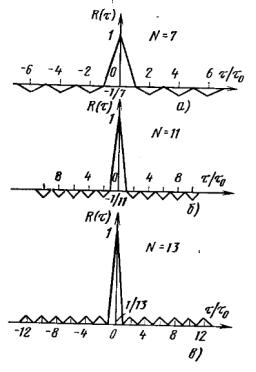
Комплексные огибающие сигнала Баркера для N = 5 и его АКФ изображены на рис. 2.1.4 (см. лекцию №4), а АКФ сигнала Баркера для N = 7, 11, 13 — на рис. 2.2.1.

Кодовые последовательности, обладающие свойством (2.1), для N > 13 не найдены.

Спектр кодовой последовательности. Амплитудный спектр H ( x )

кодовой последовательности может быть найден непосредственно из

1

выражения (4.10) (см. лекцию №4). Энергетический спектр кодовой последовательности Баркера при R (µ ) = 1 / N описывается выражением

где x = ωτ 0 .

Рис. 2.2.1. АКФ сигналов Баркера с N = 7, 11, 13

Формирование и обработка сигналов Баркера. Формирование сигналов Баркера может осуществляться несколькими способами, так же, как и произвольного ФМн сигнала. Поскольку сигналы Баркера были первыми ШПС, причем с наилучшими АКФ, рассмотрим кратко один из возможных способов формирования и обработки сигналов Баркера.

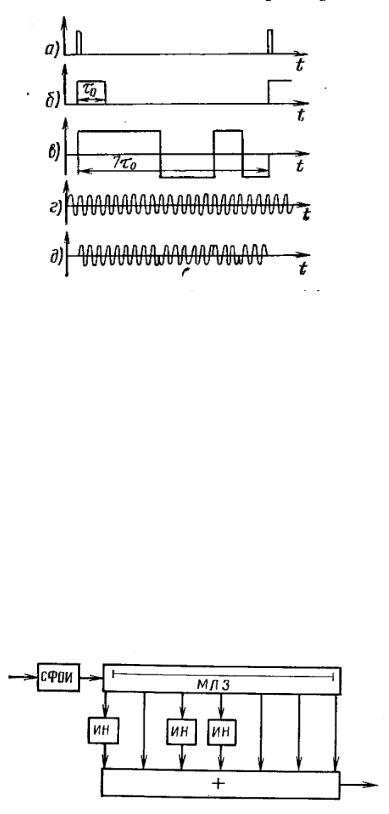
На рис. 2.2.2 изображен генератор сигнала Баркера с N = 7. Генератор синхроимпульсов (ГСИ) формирует узкие прямоугольные синхроимпульсы (рис. 2.2.3,а), период следования которых равен длительности сигнала Баркера , а τ0 — длительность одиночного (единичного) прямоугольного импульса. Генератор синхроимпульсов запускает генератор одиночных импульсов (ГОИ), который в свою очередь формирует одиночные прямоугольные импульсы длительностью τ0 и периодом Т (рис 2.2.3,б). Одиночные прямоугольные импульсы поступают на вход многоотводной

2

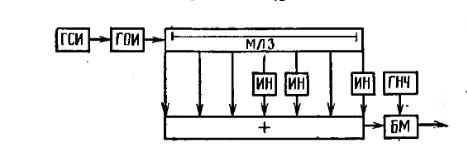
линии задержки (МЛЗ), которая имеет N – 1 = 6 секций с отводами через интервалы времени, равные τ0. Число отводов, включая начало линия, равно 7. Так как кодовая последовательность Баркера с N = 7 имеет вид 1 1 1 –1 –1 1 –1, то импульсы с первого, второго, третьего и шестого отводов (счет ведется от начала линии) поступают на вход сумматора ( + ) непосредственно, а импульсы с четвертого, пятого и седьмого отводов поступают на вход сумматора через инверторы (ИН), которые превращают положительные одиночные импульсы в отрицательные, т. е. осуществляют изменение фазы на π. Поэтому инверторы называются также фазовращателями. На выходе сумматора имеет место видеосигнал Баркера (рис. 2.2.3, в), который затем поступает на один вход балансного модулятора (БМ), на другой вход которого подается радиочастотное колебание (рис. 2.2.3, г) на несущей частоте, формируемое генератором несущей частоты (ГНЧ). Балансный модулятор осуществляет фазовую манипуляцию радиочастотного колебания ГНЧ в соответствии с кодовой последовательностью Баркера: видеоимпульсу с амплитудой 1 соответствует радиоимпульс с фазой 0, а видеоимпульсу с амплитудой –1 — радиоимпульс с фазой π. Таким образом, на выходе балансного модулятора имеет место радиочастотный сигнал Баркера (рис. 2.2.3,д). Следует отметить, что в генераторе сигнала Баркера многоотводная линия задержки (рис. 2.2.2) является видеочастотной.

Рис. 2.2.2. Генератор сигнала Баркера с N = 7

Оптимальная обработка сигналов Баркера так же, как и других ШПС, производится либо с помощью согласованных фильтров, либо с помощью корреляторов. Возможно несколько способов построения согласованных фильтров и корреляторов, отличающихся друг от друга в техническом выполнении, но обеспечивающих одно и то же максимальное отношение сигнал-помеха на выходе. На рис. 2.2.4 приведена схема согласованного фильтра для сигнала Бартера с N = 7. С выхода усилителя промежуточной частоты приемника (на схеме рис. 2.2.4 приемник не показан) сигнал поступает на согласованный фильтр одиночного импульса (СФОИ), который

3

производит оптимальную обработку (фильтрацию) одиночного прямоугольного радиоимпульса с центральной частотой, равной промежуточной частоте приемника.

Рис. 2.2.3. Временные диаграммы процесса формирования сигнала Баркера с N = 7

На выходе СФОИ радиоимпульс имеет треугольную огибающую (см. рис. 1.11.1). Треугольные радиоимпульсы с длительностью по основанию 2τ0 поступают на МЛЗ, которая имеет 6 секций и 7 отводов (включая начало линии). Отводы следуют через τ0. Так как импульсная характеристика согласованного фильтра совпадает с зеркально отраженным сигналом, то кодовую импульсную характеристику фильтра для сигнала Баркера с N = 7 следует устанавливать в соответствии с последовательностью –1 1 –1 –1 1 1 1. Поэтому радиоимпульсы со второго, пятого, шестого и седьмого отводов МЛЗ поступают в сумматор ( + ) непосредственно, а радиоимпульсы с первого, третьего и четвертого отводов — через инверторы (ИН), которые меняют фазу на π. На выходе сумматора имеет место АКФ сигнала Баркера, огибающая которой приведена рис. 2.2.1.

Рис. 2.2.4. Согласованный фильтр сигнала Баркера с N = 7

4

Необходимо отметить, что при оптимальной обработке радиочастотного сигнала Баркера все элементы схемы рис. 2.2.4 являются радиочастотными, т. е. СФОИ, МЛЗ, ИН и сумматор должны работать на промежуточной частоте и иметь необходимую полосу пропускания, которая определяется шириной спектра сигнала Баркера.

Если сигналы Баркера используются в электросвязи, т. е. их передача осуществляется по широкополосному кабелю, то в схеме генератора, изображенной на рис. 2.2.4, нет необходимости в ГНЧ и БМ, а все элементы схемы согласованного фильтра (рис. 2.2.4) являются видеочастотными, в том числе и МЛЗ.

2.3. М-последовательности. Основные свойства

Среди фазоманипулированных сигналов особое место занимают сигналы, кодовые последовательности которых являются последовательностями максимальной длины или М-последовательностями. Такие последовательности обладают следующими основными свойствами:

1.М-последовательность является периодической с периодом, состоящим из N импульсов (символов).

2.Боковые пики периодической автокорреляционной функции сигналов, образованных М-последовательностью, равны –1/N.

3.М-последовательность в общем случае состоит из нескольких видов импульсов (например, импульсы могут отличаться начальными фазами, несущими частотами и т. д.). Импульсы различного вида встречаются в периоде примерно одинаковое число раз, т.е. все импульсы распределяются в периоде равновероятно. Вследствие этого М-последовательности называют часто псевдослучайными.

4.Формируются М-последовательности с помощью линейных переключательных схем на основе сдвигающих регистров. При этом, если применяется регистр с k разрядами и в М-последовательности используются

рразличных видов импульсов (отличающихся, например фазами), то

увеличение числа импульсов N в периоде М-последовательности вызывает незначительное увеличение числа разрядов регистра, так как зависимость k от N является логарифмической.

5. Автокорреляционная функция усеченной М-последовательности, под которой понимается непериодическая последовательность длиной в период

5

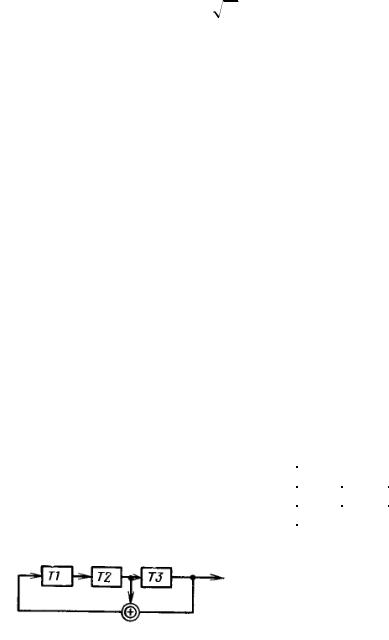
N, имеет величину боковых пиков, близкую к 1 / N . Поэтому с ростом N величина боковых пиков уменьшается.

Благодаря перечисленным свойствам М-последовательности широко применяют в радиотехнических системах. Для пояснения этих свойств рассмотрим пример.

Допустим, что сдвигающий регистр (рис. 2.3.1) состоит из трех триггерных ячеек Т1, Т2, Т3, которые выполняют роль дискретных элементов задержек, и сумматора. На триггеры поступают сдвигающие импульсы, которые на рис. 2.3.1 не показаны. Они следуют с тактовой частотой 1/τ0. Каждый тактовый импульс вызывает изменение состояния (напряжения на выходе) всех триггеров. При этом напряжение на выходе каждого триггера (символ) становится равным напряжению (символу) на его входе для предыдущего такта. Символы могут принимать два значения, которые условно обозначим 0 и 1. При суммировании любых комбинаций входных символов на выходе сумматора получаются только символы 0 и 1. Правило суммирования символов в двоичной системе счисления (с двумя возможными значениями символов) по модулю 2 (mod2) определяется табл. 2.3.1.

Таблица 2.3.1. Суммирование по mod2

Рис. 2.3.1. Генератор М-последовательности с N = 7

Выясним, в каких состояниях может находиться схема, представленная на рис. 2.3.1. Предположим, что в исходном состоянии символ на одном из выходов триггеров отличается от нуля, например символ на выходе триггера Т1 имеет значение 1, а на выходе Т2 и ТЗ — значение 0. Тогда исходное состояние сдвигающего регистра характеризуется комбинацией выходных символов 100. На входе Т1 символ равен 0, так как согласно с табл. 2.3.1 символ на выходе сумматора равен 0 0 = 0 . С поступлением на вход схемы очередного сдвигающего импульса символы со входов триггеров «переходят» на их выходы. Новое установившееся состояние регистра описывается комбинацией выходных символов 010. На входе Т1 появляется 1, так как в соответствии с табл. 2.3.1 выходной символ сумматора равен

6

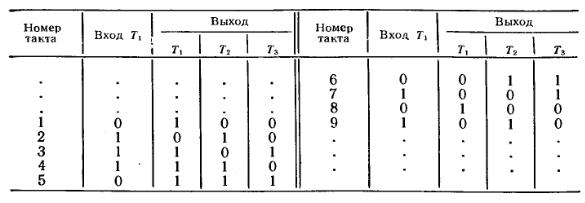
1 0 = 1 . Аналогично определяются все состояния регистра, приведенные в табл. 2.3.2.

Из рассмотрения табл. 2.3.2 видно, что состояния регистра (символы на выходе Т1, Т2, Т3) различны для тактов 1-7, а для последующих тактов они повторяются. Так как число разрядов регистра k = 3, а основание системы счисления (число используемых символов) р = 2, то число возможных различных состояний регистра pk = 23 = 8 .

В табл. 2.3.2 отсутствует нулевая комбинация 000, так как её наличие согласно табл. 2.3.1 приводит к обращению в нуль всех символов во всех остальных комбинациях. Поэтому в табл. 2.3.2 приведены только возможные для нормальной работы схемы (рис. 2.3.1) состояния регистра, число которых 23 – 1 = 7. После семи тактов состояния регистра повторяются. Если символы непрерывно считывать со входа Т1, то получим периодическую последовательность

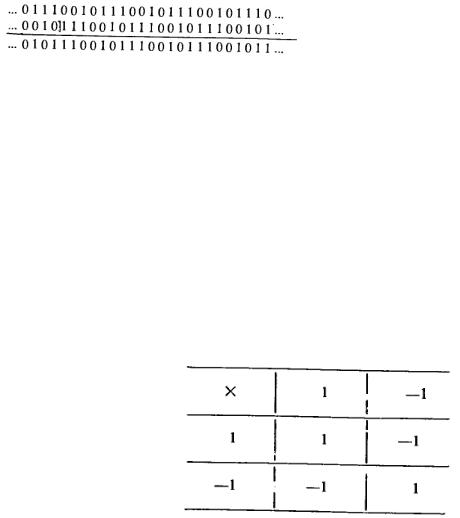
...0111001011100101110... (2.5)

с периодом, равным N = 7. Отметим, что символы можно считывать с выхода любого триггера. В этом случае получаются последовательности, сдвинутые во времени (табл. 2.3.2).

Таблица 2.3.2. Состояния регистра

Подчеркнем, что период последовательности (2.5) является максимально возможным для данного числа разрядов (триггеров) схемы рис. 2.3.1 и выбранного основания системы счисления. Это следует из того, что в регистре последовательно сменяются все возможные состояния, кроме нулевого. Период N = 7 для последовательности (2.5) совпадает со значением, определяемым формулой (2.4), при k = 3 и р = 2.

Необходимо отметить, что при заданных k и р период последовательностей вида (2.5) определяется схемой включения отводов сдвигающего регистра (выходов триггеров) в цель обратной связи. Он может быть получен и меньше максимально возможного. Выбор соединений отводов сдвигающего регистра в цепи обратной связи для получения

7

максимального периода последовательности при заданном числе разрядов регистра и основания системы счисления к настоящему моменту полностью определен и решается с помощью таблиц неприводимых многочленов.

При рассмотрении работы схемы рис. 2.3.1 было сделано допущение, что исходное состояние регистра характеризуется комбинацией 100. Из табл. 2.3.2 видно, что в качестве исходного можно взять любое состояние регистра. Это вызовет лишь сдвиг последовательности (2.5) во времени.

Число единиц и нулей в периоде последовательности (2.5) соответственно 1 = 4 , 0 = 3 , причем 1 + 0 = N . Отметим, что отличие между µ1 и µ0 на единицу в последовательностях вида (2.5) имеет общий характер. В общем случае при р = 2 число единиц в последовательности равно 2k–1, а число нулей 2k–1 – 1.

Сумма двух М-последовательностей, сдвинутых друг относительно друга, является М-последовательностью. В этом можно убедиться, суммируя согласно правилам табл. 2.3.1 последовательность (2.5) и, например, М-последовательность с выхода Т3 на рис. 2.3.1, т. е.

(2.6)

Это является следствием того, что сдвинутые М-последовательности можно получить с помощью одной и той же схемы.

Фазоманипулированный сигнал с помощью М-последовательностей формируется следующим образом. Каждому символу последовательности ставится в соответствие радиоимпульс со своей начальной фазой. В двоичной системе счисления (р = 2) это соответствие можно определить как

0 ei 0 = 1

(2.7)

1 eiπ = −1

где двойная стрелка означает соответствие.

В соответствии с (2.7) табл. 2.3.1 сложения символов 0 и 1 превращается в таблицу умножения символов 1 и –1 (табл. 2.3.3).

Таблица 2.3.3. Умножение символов

8

АКФ периодического ФМн сигнала определяется согласно (4.23) (см. лекцию №4), где an = ±1 . Обозначая символы М-последовательности (2.5)

последовательностей является тоже М-последовательностью. Но в ней число единиц в периоде на единицу больше числа нулей. Поэтому сумма по всем bn bn − при N = 1, ..., N будет равна единице, а в выражении для АКФ (4.23)

сумма будет равна согласно (2.7) –1/N. При = lN для любого l=0, 1, ...

ременной сдвиг между двумя М-последовательностями равен нулю. При этом из (4.23) получаем, что R ( ) = 1.

Объединяя полученные результаты, получаем

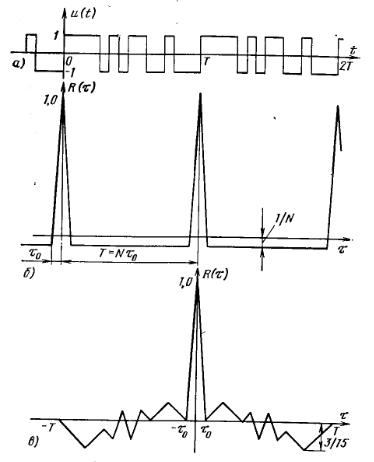
На рис. 2.3.2,а изображена М-последовательность с N = 15, на рис. 2.3.2,б — периодическая АКФ, дискретные значения которой построены согласно (2.9), а рис. 2.3.2,в — апериодическая АКФ.

Рис. 2.3.2. М-последовательность с N = 15 (а), периодическая АКФ (б), апериодическая АКФ (в)

9

Рассмотренный пример подтвердил основные особенности М- последовательности.

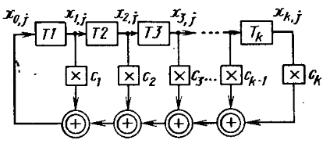
Цифровой автомат формирования М-последовательностей. Общая схема цифрового автомата, формирующего М-последовательность, приведена на рис. 2.3.3. Его основу составляет сдвигающий регистр с триггерами Т1, Т2,

.... , Т7, которые осуществляют задержку входного символа на один такт длительностью τ0. Допустим, что используются р различных символов: 0, 1,2,

обозначен x0, j. Символ на выходе 1-го триггера на (j+1)-м такте xl, j + 1 = xl - 1, j, так как с каждым тактом символ со входа «переходит» на выход. Символы с

выходов триггеров поступают на умножители, с выходов которых снимают символы c1 x1, j , c2 x2, j , ..., ck xk , j . Множители cl S . Поэтому, если операция умножения в множителе производится по модулю p(mod p), то символы cl xl , j S . Смысл умножении по модулю становится понятным при

рассмотрении сравнения двух чисел по третьему числу (модулю). Два целых числа а и b называются сравнимыми по модулю р, если при делении обоих чисел на р их остатки равны. Сравнение двух чисел обозначается как

Рис. 2.3.3. Цифровой автомат формирования М-последовательности

Остаток от деления любого числа на р всегда меньше р и лежит в пределах от 0 до р – 1. Например, если р = 5, то 12 ≡ 2 (mod 5) , так как остатки

от деления обоих чисел равны двум. Сравнение (2.10) означает, что разность а — b делится на р без остатка, что иногда записывается a − b ≡ 0 (mod p ) .

Таким образом, сравнение по модулю р означает перевод произвольного целого числа в конечное множество S, состоящее из р элементов.

Умножение двух чисел по модулю р производится следующим образом. Два числа перемножаются обычным образом, а их произведение

10