Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Балтийский федеральный университет им. И.Канта

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Глава_7_Приложение_произв

.pdf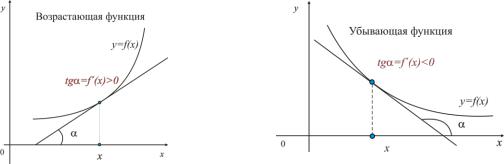

Скачиваний:

Добавлен:

10.02.2015

Размер:

1.42 Mб

Скачать

☆

1 / 31 2 3 > Следующая >>>

119

Глава 7 Приложения производной

§1 Возрастание и убывание функций

Теорема 1.1. Для того, чтобы дифференцируемая на a; b функция не

убывала (не возрастала) на этом интервале необходимо и достаточно, чтобы
f x 0 f x 0 для всех x a; b . Если же для любого x a; b	f x 0

( f x 0 ), то функция f x возрастает (убывает) на этом интервале. Другими словами:

1)f x не убывает на a; b x a; b : f x 0 ;

2)f x не возрастает на a; b x a;b : f x 0 ;

3) Если x a;b : f x 0 , то			f x	возрастает на a; b ;
4) Если x a;b : f x 0 , то			f x	убывает на a; b ;
1. Рассмотрим случай неубывающей функции
	Необходимость: Пусть		f x не убывает на a; b . Тогда для любого
x a; b	при x 0
	y f x x f x 0		y 0 lim			y	f x 0 x a; b
			x		x 0	x
	Достаточность. Пусть		f x 0		любого x a; b .			Тогда по формуле
Лагранжа имеем		f x2 f x1 f x2 x1

Так как	f 0 x1 x2 , то x1 , x2 a; b :x1 x2						f x2 f x1 0 ,		т.е. функция
не убывает.
2. Докажем теорему для случая возрастающей функции.
Пусть	f x 0 тогда	a; b	f 0		и		поэтому	x1 , x2	a; b :x1 x2
f x2 f x1 f x2		x1 0 т.е.	f x	возрастает на a; b .
Геометрический		смысл теоремы		состоит		в	следующем: касательная к

графику возрастающей на a; b функции составляет острый угол с осью ОХ; касательная к графику убывающей на a; b функции составляет тупой угол с осью ОХ (Рис. 1.1 и 1.2).

Рис. 1.1	Рис. 1.2
					1

Пример. Найти интервалы возрастания и убывания функции		f	x	1	x 2 .
Пример. Найти интервалы возрастания и убывания функции		f	x	1	x 2 .

120

Данная функция определена и дифференцируема на всей числовой прямой. Находим производную функции

2 1

f (x) 1 x

1 1 x

(x)

x2 2

при x ;0 возрастает и убывает

Следовательно, функция

x 2

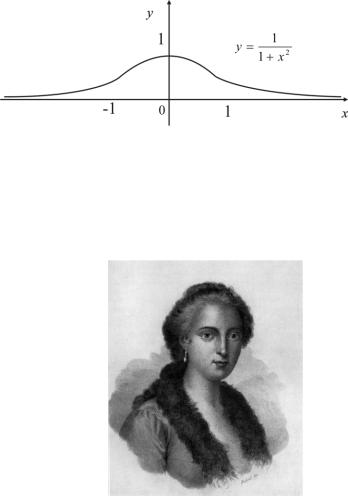
при x 0; . График этой функции изображен на рисунке 1.3

Рис. 1.3

График этой функции называется локоном Аньези.

Мария Гаэтано Аньези (Agnesi Maria Gaetana1718-1799) опубликовала описание данной кривой в 1748 году в труде «Основания анализа для употребления итальянского юношества».

§ 2 Точки локального экстремума функции.

Необходимые и достаточные условия существования экстремума функции

Экстремум функции.

Особую роль при исследовании функций играют точки, разделяющие интервалы возрастания и убывания функции.

121

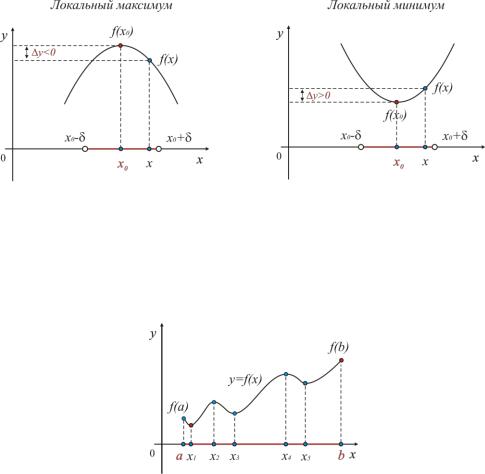
Определение 2.1. Точка x0 называется					точкой локального максимума
(Рис. 2.1) (минимума Рис. 2.2) функции			f x ,		если существует -окрестность
точки x0 , такая, что для вех x O x0		выполняется неравенство

f x f x0			f x f x0
Значение f x0 называют	локальным максимумом (минимумом) функции и
пишут	f x f x0			f x f x0 )
max		(	min
x O x0			x O x0

Точки максимума или минимума называют экстремумами функции.

Рис. 2.1 Рис. 2.2

Наибольшее и наименьшее значения функции на [a;b] называют абсолютным максимумом и минимумом (Рис. 2.3) и пишут

max f x	f x			f x f x
max f x	f x		min	f x f x
x [a;b]		0	x [a;b]		0

Рис. 2.3

На рисунке 2.3 в точках x1 , x3 , x5 - локальные минимумы, в точках x2 , x4 - локальные максимумы, в точке x1 достигается абсолютный минимум (наименьшее

значение), а точке b – абсолютный максимум (наибольшее значение) функции на отрезке [a;b].

Необходимое условие существования экстремума функции.

Теорема 1.2. Если в точке x0 функция f x достигает экстремума то ее производная в этой точке или равна нулю или не существует.

	пусть	f x достигает в точке x0 максимума. Тогда существует такая
	, что
O x0	, что

122

x0 f x0 f x0 x , x 0.

x O

При x 0

f x0 x f x0

0 ,

при x 0

f x0 x f x0

0 ,

Если пределы левых частей этих неравенств существуют, то

lim

f x0

0 0 ,

x 0

lim

f x0

x f

f x

0 0

x 0

Если производные функции

f x0 0 в

точке x0

равны

нулю, то

существует

f x0 f x0 0 f x0 0 =0.

Если

производные

f x0

f x0 0 не равны нулю

то f x0 не

существует.

Аналогично можно доказать случай, когда x0 -точка минимума.

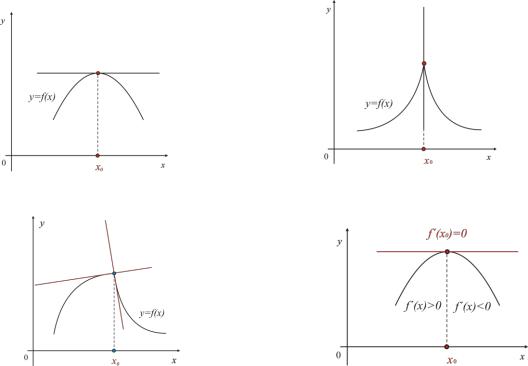
Геометрический смысл теоремы 1.2 заключается в следующем: в точках

локального экстремума функции f x			касательная к ее графику параллельна оси
абсцисс (Рис 2.4),	если	существует	f x0 0 ;	параллельна оси ординат, если
f x0 бесконечна	(Рис.	2.5), существуют не		совпадающие левая и правая
касательные, если	f x0	0 f x0 0	(Рис. 2.6).

Рис. 2.4

Рис. 2.5

Рис. 2.6	Рис.	2.7
Точки, в которых	производная функции обращается в	ноль или не

существует называются критическими точками (или точками возможного экстремума). Точки, в которых производная обращается в ноль называются

стационарными точками.

123

Критическая точка

называется

угловой точкой

функции

f x , если

f x0

0 f x0

0 . Критическая точка x0

называется точкой возврата функции

если

f x0 0 и

f x0

0 бесконечны.

Достаточные условия существования экстремума

Терема 2.2 (первый достаточный признак существования экстремума

функции). Пусть x0

критическая точка непрерывной функции f x .

Если f x

при переходе через

точку

меняет знак с "+" на "-", то

точка x0 - точка

локального максимума; если f x при переходе через точку x0

меняет знак с "-" на

"+", "-", то точка x0 - точка локального минимума; если

f x

при переходе через

точку x0 не меняет знака то x0 не является точкой локального экстремума.

Пусть x0 - точка возможного экстремума,

причем

f x 0 x O x0 0 и

f x 0 x O x0 0 . Тогда

f x 0 x O

0 f x

f (x)

f x

: f

f x 0 x O

0 f x

f (x)

т.е. точка x0 является точкой локального максимума (Рис 2.7).

Аналогично доказывается и существование точки локального минимума.

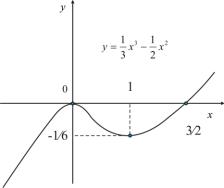
Пример 2.1. Найти экстремумы функции f (x) 13 x3 12 x 2

Найдем производную функции:

f x x2 x

Для нахождения нулей производной и промежутков ее знакопостоянства (а значит стационарных точек и промежутков монотонности функции) решим уравнение:

						x 0,
			x		x 0
		f x 0	x	2	x 0
						x 1
Составим следующую таблицу:
х	x<0	0				0<x<1	1	x>1
f´(x)	+	0				-	0	+
f(x)	возрастает	максимум				убывает	минимум	возрастает
f(x)		0					-1/6

По этим результатам можно схематично изобразить график функции (Рис.8.2):

124

Рис. 2.8

Терема 2.3 (второй достаточный признак существования экстремума).

Стационарная точка

функции

f x ,

дважды

дифференцируемой

O x0 ,

является точкой локального минимума, если

f x0 0 ,

и точкой

локального

максимума, если

f x0 0 .

O x0

Пусть выполнены условия теоремы и

Тогда

f x в

возрастает,

но f x0 0 , следовательно,

в O x0

f x

меняет знак с "-" на "+".

Согласно теореме 2.2 это означает, что точка

является точкой

локального

минимума.

f x0 0 ,

O x0

f x0 0 ,

Если

то

f x в

убывает,

но

следовательно,

f x в O x0 меняет знак с "+" на "-". Тогда согласно теореме 3 это означает, что

точка x0 является точкой локального максимума

Теорема 2.4. (третий достаточный признак существования экстремума

функции).

f x

Пусть функция

- n

раз непрерывно дифференцируема в точке x0 и

f x

... f n 1 x

n x

0 . Тогда:

1) если n - четное и

f n x 0 , то x

- точка локального максимума;

2) если n - четное и

f n x 0 , то x0 - точка локального минимума;

3) если n - нечетное то x0

не является точкой локального экстремума;

Доказательство.

Воспользуемся формулой Тейлора с остаточным членом в форме Пеано

n x

f x f x0

x x0

o x x x0 ,

где o x 0 , при x x0 . Преобразуем последнее выражение:

f n x0

f x f x

o x x x

В силу бесконечной малости o x

выражение

n x

o x

будет иметь такой же

f n x

знак, что и

Рассмотрим

случай,

когда

четное.

Тогда

приращение

функции

f x f x f x0

при переходе x

через точку x0

не будет менять знак.

	125
Если f n x0 0 , то	f x f x f x0 0 , следовательно,		f x f x0 и в
точке x0 - минимум. Если же f n x0 0 , то		f x f x0 и в точке x0	- максимум.

В случае, когда n- нечетное число приращение функции при переходе x через

точку x0 будет менять знак, следовательно, в точке x0

нет экстремума.

Теорема доказана.

Пример 2.2. Найти локальные экстремумы функции f x x 4

4x 3

Данная функция определена, непрерывна и дифференцируема на всей

числовой прямой. Найдем стационарные точки

f x 4x 3 12x 2 , 4x 3 12x 2 0 x

0, x

1,2

f x 12x 2 24x, f 3 36 0, f 0 0

Стационарная точка x=3 является точкой локального минимума.

Найдем производные высших порядков

f x 24x 24

Согласно

теореме 5 точка x=0

не

является

точкой локального

0 24

экстремума.

§. 3 Абсолютные экстремумы функции на отрезке

Одной из основных характеристик функции на отрезке являются ее

абсолютные экстремумы, т.е. наибольшее и наименьшее значения

f x на отрезке

[a;b].

Если функция f x непрерывна на [a;b]..то она принимает наибольшее и

наименьшее значения она принимает на концах этого отрезка или в точках ее

локальных экстремумов.

Если x1 , x2 ,..., xn - точки локальных экстремумов, то

, f x

,..., f x

min

f x min

f a , f b , f x

x a;b

, f x

,..., f x

max f x max

f a , f b , f x

x a;b

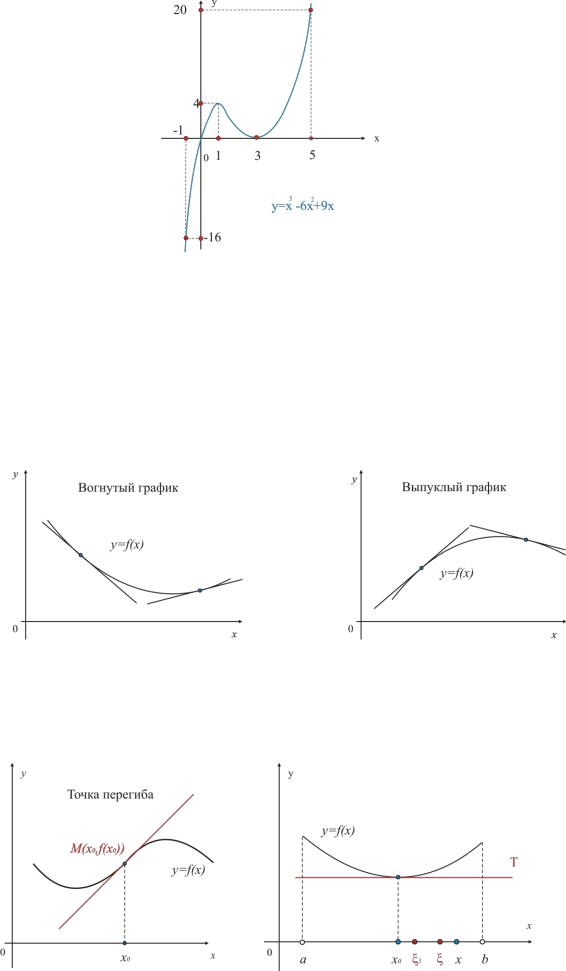
9x на 1;5 .

Пример 3.1. Найти абсолютные экстремумы функции

f x x 3 6x 2

Найдем стационарные точки функции

x 1,

4x 3 0

f x 3x

12x 9 f x 0 x

x 3.

Вычислим значения функции в стационарных точках и на концах отрезка

f 1 4, f 3 0, f 1 16, f

Исходя из этих значений, приходим к выводу, что

min

f x f 1 16 ,

x 1;5

max f x f 51 20/

x 1;5

График данной функции можно изобразить на следующем рисунке 3.1

126

Рис. 3.1

§4 Исследование функций на выпуклость и вогнутость. Точки перегиба

Определение 1.4. График дифференцируемой функции y	f x называется
выпуклым вниз (или вогнутым) на (a;b), если дуга кривой	y f x x a; d

расположена выше любой касательной, проведенной к графику этой функции (Рис. 4.1)

Рис. 4.1 Рис. 4.2

Определение 4.2. График дифференцируемой функции y f x называется выпуклым вверх (или выпуклым) на (a;b), если дуга кривой y f x x a; d расположена ниже любой касательной, проведенной к графику этой функции (Рис

4.2).

127

Рис. 4.3

Рис. 4.4

Определение

4.3

Точка

M x0 ,

f x0

графика

дифференцируемой

функции

y f x ,

в которой направление

выпуклости меняется на противоположное

называется, точкой перегиба (Рис. 4.3).

Теорема 4.1

Если функция

y f x на (а;b) дважды дифференцируема и

f x 0

x a; b ,

то график этой кривой вогнутый (выпуклый вниз). Если

f x 0

x a; b , то график этой кривой выпуклый на (а;b).

Пусть на интервале (a;b)

f 0

0 . Возьмем точку x0

a; b и покажем, что все

точки графика функции y f x на (a;b)

лежат выше касательной, проведенной к

нему в точке x0

(Рис. 4.4)

Уравнение касательной

Y f x0

f x0 x x0

Y f x0 f x0 x x0 ,

где Y -ординаты точек касательной. Разность ординат точек кривой и касательной

y Y f x f x0 f x0 x x0

Применяем формулу Лагранжа к функции f x на

x; x0 , получаем

y Y f x x0 f x0 x x0 y Y f f x0 x x0 ,

где

x0 , x a; b . Применим формулу Лагранжа к разности

f f x

на

x0 , , находим

y Y f 1 x0 x x0 ,

где

1 x0 ; a; b . В последнем равенстве

f 1 0 ,

а x0 0 , если x x0

0 ,

или

0 , если x x0 0 . Следовательно,

y Y т.е. ординаты точек кривой больше

ординат точек касательной при одной и той же абсциссе. Точки кривой y f x на

a; b лежат выше точек касательной к кривой.

График функции y f x на a; b вогнутый.

Доказательство выпуклости проводится аналогично.

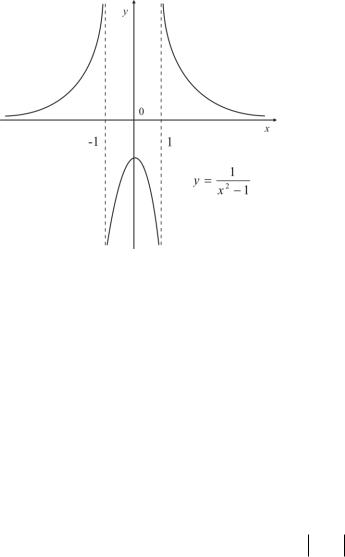
Пример.

Найти интервалы

выпуклости и

вогнутости графика

функции

f x

Находим первую производную: f x

;

x2 1 2

3x2 1

x 1 3 (x 1)3

Вторая производная f

x 2

x 0, x ; 1 1; , график кривой вогнутый

(Рис. 4.5).

x 0, x 1; 1 - график кривой выпуклый

128

Рис. 4.5

Сформулируем достаточные условия существования точек перегиба

Теорема 4.2. Если для функции f x вторая производная f x в некоторой

точке x0 обращается в ноль или не существует и при переходе через неё меняет

свой знак, то точка M x0 , f x0 является точкой перегиба графика функции.

0 в

Пусть f x0 0 или не существует. Если f

O x0 0 и f

в O x0 0 , то точка кривой с абсциссой

x0 отделяет интервал выпуклости от

0 в O x0

в O x0 0 , то точка

интервала вогнутости. Если f x

0 и f

кривой с абсциссой x0 отделяет интервал вогнутости от интервала выпуклости. В обоих случаях точка M x0 , f x0 является точкой перегиба графика функции.

Пример. Найти точки перегиба графика функции f x 1 x3 1 . Раскроем абсолютную величину числа

					3	, x 1
f x 1	x	3	1	x		, x 1
f x 1	x		1
								2, x 1

				x			3
							3

Найдем первую и вторую производные:

			2	, x 1
		3x		, x 1
f	x						,
					2
		3x			2	2, x 1
		3x				2, x 1

6x, x 1, f x

6x, x 1.

Отметим, что в единице первая и вторая производные не существуют. f x 0, x ;0 1; , график кривой выпуклый,

f x 0, x 0;1 - график кривой вогнутой. В точках 0 и 1 вторая производная

меняет знак, следовательно точки О(0;0) и А(1;1) являются точками перегиба (Рис.

4.6).

1 / 31 2 3 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
09.07.201976.37 Кб12Глава 5. стоматологические пластмассы.Полная ве....rtf
#
17.08.2019122.88 Кб4Глава 5.doc
#
09.07.201993.38 Кб15Глава 7. Основные металлы и сплавы.rtf
#
09.07.201963.74 Кб13Глава 9. Вспомогательные материалы.rtf
#
16.08.2019367.62 Кб7Глава6.doc
#
10.02.20151.42 Mб12Глава_7_Приложение_произв.pdf
#
23.03.201617.58 Mб31Гласс, Эйблс - UNIX для программистов и пользователей.djvu
#
18.11.201889.6 Кб5Глобализация международной экономики.doc
#
17.09.2019216.06 Кб2Глоссарий по европейской интеграции.doc
#
10.02.201556.32 Кб88Глоссарий по метрологии.doc
#
10.02.2015144.9 Кб7Глоссарий-ПМ.doc