
Глава_7_Приложение_произв
.pdf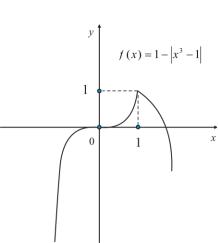
129
Рис. 4.6
§5 Асимптоты графика функции
При исследовании поведения функции на бесконечности или вблизи точек разрыва второго рода часто оказывается, что расстояния между точками графика и точками некоторой прямой бесконечно малы. Такую прямую принято называть асимптотой графика.
Определение 5.1 Асимптотой графика функции называется такая прямая, для которой расстояние между графиком и точкой прямой, стремится к нулю по мере удаления точки от начала координат.
Различают асимптоты горизонтальные, вертикальные и наклонные. |
|
|
|
|||
Прямая |
x x0 называется |
вертикальной асимптотой |
графика |
функции |
||
y f x если |
хотя бы один из односторонних пределов |
в точке |
x0 |
равен |
||
бесконечности, т.е. |
|
|
|
|
|
|
|
lim f x или lim f x |
|
|
|
|
|
|
x x0 0 |
x x0 0 |
|
|
|
|
Очевидно, что непрерывные функции вертикальных асимптот не имеют; |
||||||
такие асимптоты существуют только в точках разрыва второго рода. |
|
|
|
|||
Пример 5.1. Найти вертикальные асимптоты графика функции y |
1 |
. |
||||
|
|
|||||
x 2 |
1 |
|||||
Прямая |
y kx b называется наклонной (если k=0 |
– горизонтальной) |
||||
асимптотой графика функции y f x при x x , если функцию f x |
||||||
можно представить в виде f x kx b x , где x 0 при x x . Теорема 5.1. Для того, чтобы график функции y f x имел наклонную
асимптоту y kx b , необходимо и достаточно, чтобы существовали конечные пределы:
lim |
f x |
k, |
lim |
f x kx b |
(5.1) |
||
x |
|||||||
x |
|
x |
|
|
|
||
Необходимость Предполагаем, что |
y kx b |
- наклонная асимптота |
|||||
графика функции y f x . Тогда функцию можно представить в виде
130
f x kx b x
где x 0 при x . Следовательно,
|
f x |
|
b |
|
x |
|
|
lim |
|
lim k |
|
|
|
k, |
|
x |
x |
||||||
x |
x |
|
x |
|
lim f x kx lim b x b. |
|
x |
x |
Достаточность. Пусть существуют пределы (5.1) тогда по свойствам предела функции получаем
f x kx b x f x kx b x
что и означает, что прямая y kx b |
- наклонная асимптота графика функции |
||||||||||||
y f x |
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 5.2 Найти асимптоты функции y |
|
|
1 |
. |
|||||||||
|
|
||||||||||||
1 x 2 |
|||||||||||||
Найдем пределы функции на бесконечности: |
|
|
|
|
|
||||||||
lim |
|
1 |
|
0, lim |
|
1 |
|
|
0 |
||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
x2 |
|
||||||||
x 1 x2 |
|
|
x 1 |
|
|
|
|||||||
Следовательно, ось ОХ является двусторонней горизонтальной асимптотой. |
|||||||||||||
k lim |
f |
x |
lim |
|
1 |
|
|
0, |
|||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
x2 |
|
|||||||
x |
|
x |
|
|
x x 1 |
|
|
||||||
b lim f (x) kx 0
x
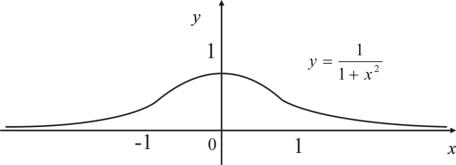
Других асимптот нет. Напомним, что график кривой имеет специальное название «Локон Аньези»
Рис. 5.1 |
|
|
|
Пример 5.3. Найти асимптоты функции |
y |
x2 |
x 1 |
|
x 1 |
||
|
|
|
В точке x 1 функция терпит разрыв. Найдем односторонние пределы
lim |
x2 |
3x 6 |
, lim |
x2 |
3x 6 |
. |
|
x 1 |
|
x 1 |
|||
x 1 0 |
|
x 1 0 |
|
|
Следовательно, прямая x 1 является вертикальной асимптотой. Ищем параметры наклонной асимптоты
k lim |
f x |
lim |
x2 x 1 |
1, |
|||
x |
|
x x 1 |
|
||||
x |
x |
|
|||||
131
|
|
|
2 |
x 1 |
|
||
b lim f (x) kx lim |
x |
|
|
||||
|
|
|
x 1 |
|
|||
x |
x |
|
|
|
|||
|
|
|
|
|
|
||
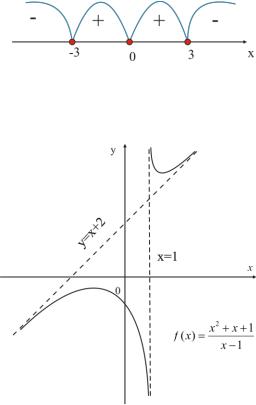
Наклонная асимптота имеет уравнение y x 2 .
А сам график изображен на рисунке 5.2.
|
|
2x 1 |
|
||
|
lim |
|
|
2 . |
|
|
|
||||
x |
x 1 |
||||
|
x |
|
|
||
|
|
|
|
|
|
Знаки производной
Рис. 5.2
§6 Общая схема исследования функции
Исследование дважды дифференцируемой функции будем проводить по следующей схеме
1.Находим область определения функции D( f ).
2.Определяем точки разрыва функции.
3.Находим нули функции, точки пересечения с осями и промежутки знакопостоянства.
4.Периодичность.
5.Четность или нечетность функции.
6.С помощью первой производной определяем стационарные точки и интервалы монотонности.
7.Находим локальные экстремумы функции.
8.Исследуем поведение функции в окрестности точек разрыва и на бесконечности.
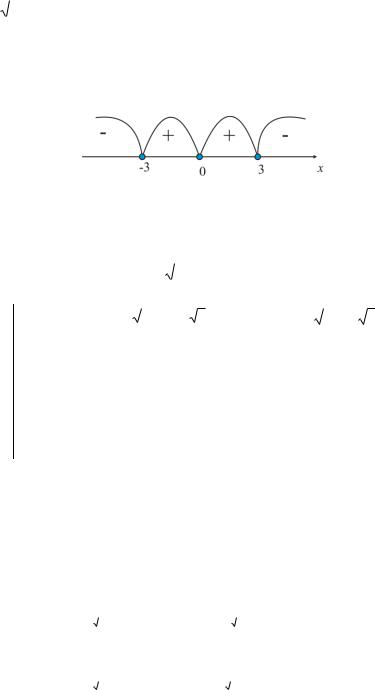
132
9. При необходимости находим значение функции в контрольных точках.
Пример. Исследовать функцию |
y |
x3 |
|
|||||||
3 x2 |
|
|
||||||||
1) D( f ) R \ |
|
|
|
|
|
|
|
|||
3 |
|
|
|
|
|
|||||
2) Функция нечетная; |
|
|
|
|
||||||
3) y |
x2 |
3 x 3 x |
Первая производная обращается в ноль при |
x 0, x 3, x 3 . |
||||||
|
3 x2 2 |
|
||||||||
|
|
|
|
|
|
|
||||
Методом интервалов рассмотрим изменение знаков у производной (Рис. 6.1)
|
6x 9 x2 |
|
|
|
|
Рис. 6.1 |
|
|
|
|
|
|
|
|
|
|
||||||||
4) y |
Точка |
перегиба |
имеет |
абсциссу |
x 0, |
|
кроме |
того, |
вторая |
|||||||||||||||
|
3 x2 3 |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
производная меняет знак в точках |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Составим таблицу: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x |
|
; 3 |
|
-3 |
3; |
3 |
|
|
|
3;0 |
0 |
|
0; |
3 |
|
|
|
|
3;3 |
|
3 |
3; |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
y |
|
- |
|
0 |
+ |
|
|
|
|
|
+ |
0 |
|
+ |
|
|
|
|
+ |
|
0 |
- |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
y |
|
+ |
|
+ |
+ |
|
|
|
|
|
- |
0 |
|
+ |
|
|
|
|
- |
|
- |
- |
||
y |
|
↓ |
|
4,5 |
↑ |
|
|
|
|
|
↑ |
0 |
|
↑ |
|
|
|
|
|
↑ |
|
-4,5 |
↓ |
|
|
|
|
|
min |
|
|
|
|
|
|
|
|
перег |
|
|
|
|
|
|
|
|
|
max |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
иб |
|
|
|
|
|
|
|
|
|
|
|
Найдем наклонную асимптоту
k lim |
|
x3 |
|
|
1 |
; |
|
x2 |
|
||||
x x 3 |
|
|
||||
|
x3 |
|
b lim |
|
|
|
2 |
|
|
3 x |
|
x |
|
x 0 .
Уравнение наклонной асимптоты: y=-x.
Находим односторонние пределы в окрестностях точек разрыва:
lim |
x3 |
, lim |
x3 |
|
|||||
3 x2 |
3 x2 |
||||||||
|
|
|
|
|
|
|
|||
x 3 0 |
x 3 0 |
|
|||||||
В силу нечетности функции, получаем
lim |
x3 |
, lim |
x3 |
|
|
3 x2 |
3 x2 |
||||
x 3 0 |
x 3 0 |
|
Исходя из полученных результатов, строим график (Рис. 6.2):

133
Рис. 6.2
§7 Интерполирование функций
Под интерполированием функции y f x на отрезке [a;b] понимают восстановление этой функции с заданной степенью точности по таблице n ее значений на [a;b] :
x |
x 0 |
|
|
x1 |
|
x 2 |
|
... |
x n 1 |
|
|
x n |
f x |
f x0 |
|
|
f x1 |
|
f x2 |
|
... |
f xn 1 |
|
|
f xn |
Точки x0 , x1 ,..., xn x0 |
a, xn b называют узлами интерполирования. |
|
|
|
||||||||
Функцию f x |
приближенно заменяют многочленом |
|
|
|
|
|||||||
|
|
|
|
Pn x a0 x n a1 x n 1 ... an , |
|
|
(7.1) |
|||||
значения которого совпадают со значениями |
f x в узлах интерполирования (Рис. |
|||||||||||
7.1): |
|
|
|
|
Pn xi f xi |
|
|
|
|
|
|
|
|
|
|
|
|
i 0,1,2,..., n . |
|
|
(7.2) |
||||
Рис. 7.1
Многочлен Pn x называют интерполяционным многочленом степени n функции f x на [a;b]. Для определения неизвестных коэффициентов многочлена Pn x используем условия (7.2)

134
a |
0 |
x n a x n 1 |
... a |
n |
f x |
0 |
|
|
|
|
0 |
1 0 |
|
f x |
|
|
|||
a |
0 |
x n a x n 1 |
... a |
n |
1 |
|
|||
|
1 |
1 1 |
|
|
|
(7.3) |
|||
.................................................... |
|||||||||
|
|
|
|
|
|
|
|
|
|
a |
0 |
x n a x n 1 |
... a |
n |
f x |
n |
|
|
|
|
n |
1 n |
|
|
|
|
|||
Получим систему n+1 уравнений с n+1 неизвестными. Определитель этой системы
x n |
x n 1 ... |
1 |
0 |
0 |
|
x n |
x n 1 ... |
1 |
1 |
1 |
|
....................... 0 , |
||
xnn xnn 1 ... 1
если x0 , x1 ,..., xn различны. Можно доказать, что он равен
xi x j .
0 i j n
Так определитель второго порядка
|
|
|
|
|
|
|
|
|
|
|
|
|
x0 |
1 |
x |
0 x1 ; |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
1 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
определитель третьего порядка |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
x02 x0 1 |
|
x02 |
|
|
|
|
|
|
x0 |
|
|
1 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
x |
2 |
x 1 |
|
x2 |
x |
2 |
x - x |
0 |
0 |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
1 |
|
1 |
|
|
|
1 |
|
|
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
x |
2 |
x |
2 |
1 |
|
x2 |
x |
2 |
x |
2 |
|
- x |
0 |
0 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x2 |
x2 |
x |
2 |
x |
0 |
x |
2 |
x2 |
x x |
0 |
|
x x |
0 |
|
x |
2 |
x |
0 |
x x |
2 |
|
|||||||||||||
1 |
0 |
|
|
|
|
|
|
2 |
0 |
|
1 |
|
|
|
|
|
1 |
|
|
|
1 |
|
||||||||||||
и т.д. Значит система (7.3) имеет единственное решение. Следовательно существует единственный интерполяционный многочлен Pn x , коэффициенты которого определяются из системы (7.3). Однако определение этих коэффициентов из системы (7.3) связано с громоздкими вычислениями. Для упрощения выкладок будем искать интерполяционный многочлен в виде
Pn x a0 x x1 x x2 ... x xn a1 x x0 x x2 ... x xn a2 x x0 x x1 x x3 ... x xn... an x x0 ... x xn 1 .
Будем полагать в последнем равенстве x xi i 0,1,2,..., n и учитывать
соотношения (7.2). Тогда получим коэффициенты интерполяционного многочлена: |
|||||||||||||||||||||||||||
|
|
|
|
a0 |
|
|
|
|
|
|
|
f x0 |
|
|
|
|
|
|
|
, |
|
|
|
||||
|
|
|
|
x |
0 |
x |
x |
0 |
x |
2 |
... x |
0 |
x |
n |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
a1 |
|
|
|
|
|
|
|
f x1 |
|
|
|
|
|
|
, |
|
|
|
|||||
|
|
|
|
x |
1 |
x |
0 |
x |
|
x |
2 |
... x |
|
x |
n |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
ai |
|
|
|
|
|
|
|
f xi |
|
|
|
|
|
|
|
. |
|
|
|
||||
|
|
|
|
xi |
x0 |
|
x1 |
x2 |
... xi |
xn |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Интерполяционный многочлен примет вид: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Pn |
x |
x x1 |
x x2 ... x xn |
|
|
f x0 |
|
x x0 x x2 |
... x xn |
f x1 |
|
||||||||||||||||
x0 |
x1 x0 x2 ... x0 xn |
|
x1 x0 x1 x2 ... x1 xn |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||

135
... |
x x0 x x1 ... x xn 1 |
|
|
f xn |
|
|
|
|
|||||||||
xn |
x0 |
xn x1 ... xn |
xn 1 |
|
|
|
|
||||||||||
|
|
|
|
|
|
||||||||||||
Тогда |
x x |
|
|
... x x |
|
x x |
|
|
... x x |
|
|
|
|
||||
n |
0 |
i 1 |
i 1 |
n 1 |
f xi |
|
|||||||||||
f x Pn x |
|
|
|
|
|
|
|
|
|
(7.4) |
|||||||
xi |
x0 |
|
... xi |
xi 1 |
xi |
xi 1 ... xi xn 1 |
|||||||||||
i 0 |
|
|
|
||||||||||||||
Равенство (7.4) называется интерполяционной формулой Лагранжа.
Простейшим и часто используемым приемом для работе с таблично заданными функциями является линейная интерполяция. Т.е. приближение функции многочленом первой степени.
Пример. Функция задана таблично
x |
1 |
2,5 |
3 |
4 |
f(x) |
2 |
1 |
2,2 |
3 |
Построить на отрезке [1;4] для нее интерполяционный многочлен Лагранжа
третьей степени. |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Воспользуемся формулой (7.4) |
|
|
|
|
|
|
|
||||||
P |
x f 1 |
x 2,5 x 3 x 4 |
f 2,5 |
x 1 x 3 x 4 |
|
|
||||||||
1 2,5 1 3 1 4 |
2,5 1 2,5 3 2,5 4 |
|||||||||||||
3 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
x |
|
|
|
|
x |
|
|
|
|
||
|
|
|
1 x |
2,5 |
x 4 |
|
1 x |
2,5 |
x 3 |
|
||||
|
f 3 1 2,5 1 3 1 4 f |
4 4 1 4 2,5 4 3 |
|
|||||||||||
P3 x 92 x 2,5 x 3 x 4 89 x 1 x 3 x 4
2,2 x 1 x 2,5 x 4 23 x 1 x 2,5 x 3
Окончательно получаем
P (x) |
13 |
x 3 7 |
1 |
x 2 |
17 |
3 |
x 13 |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
3 |
|
15 |
6 |
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Лагранжа для f x |
|
||||||||||||||||
После построения интерполяционного многочлена |
на |
||||||||||||||||||||||||||||
[a;b].возникает вопрос об оценке точности |
|
приближения функции f x |
|||||||||||||||||||||||||||
многочленом Pn x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Разность между функцией и ее интерполяционным многочленом |
|
||||||||||||||||||||||||||||
т.е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
rn x f x Pn x |
|
|
|
|
|
|
(7.5) |
|
|||||||||||||||||||
называется остаточным членом интерполирования. |
|
|
|
|
|||||||||||||||||||||||||
Если известно. что функция |
|
|
f x n+1 раз дифференцируема на [a;b]., |
то |
|||||||||||||||||||||||||
справедлива оценка |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
r |
|
x |
|
|
k |
|
x |
|
|
|
x [a; b], |
|
|
(7.6) |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
n 1 ! |
|
|
|
|||||||||||||||||||||
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
x x x |
|
x x ... x x |
|
|
|
|||||||||||||||||||
k max |
|
f n 1 x |
|
; |
0 |
n |
|
||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||
x [a;b] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Оценка остаточного члена интерполирования предполагает наличие информации о поведении функции на отрезке [a;b]. Чаще всего такой информации нет.
136
Вопрос о приближении функции при интерполяции сложен. Иногда при возрастании числа узлов интерполяции интерполяционный многочлен не стремится к приближаемой функции.
На практике для получения хорошего приближения функции вместо интерполяционного многочлена высокой степени используют кусочную
интерполяцию многочленами более низких степеней, т.е. на |
каждом отрезке |
|
xi , xi 1 |
строится свой многочлен. Часто используется |
кусочно-линейная |
интерполяция. Получающиеся при этом кусочно-многочленные функции с однородной структурой на каждом отрезке (многочлен одной и той же степени)
называют сплайн-функциями или просто сплайнами (от англ. Spline - рейка).
Простейший пример сплайна - ломаная.
В настоящее время в приближениях на практике чаще всего используют
кубические сплайны.
§8 Приближенное решение уравнений
Постановка задачи. Рассмотрим задачу нахождения действительных корней уравнения
f x 0 |
(8.1) |
где f x алгебраическая или трансцендентная функция.
Известные точные методы решения уравнений пригодны только для узкого класса уравнений. Однако в общем случае решения уравнения (8.1) находят приближенно.
Решение такой задачи разбивается на 2 этапа:
1)отделение корней (определение малых отрезков [a;b], в которых находится только один действительный корень уравнения)
2)приближенное вычисление отделенного корня с заданной точностью.
Отделение действительных корней.
Под отделением действительного корня уравнения f x 0 понимают нахождение отрезка [a;b], в котором лежит только один корень данного уравнения.
Этот отрезок называют промежутком изоляции корня.
Известны различные графические и аналитические методы отделения корней уравнения (8.1).
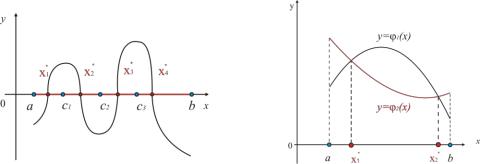
Наиболее наглядный метод отделения корней уравнения f x 0 состоит в определении (приближенно) координат точек пересечения графика функции y f x с осью абсцисс (Рис. 8.1).
Рис. 8.1 |
Рис. 8.2 |
137
На примере видно, что приближенные значения корней изолированы на
отрезках x1* a; c1 , x2* c1; c2 , x3* c2 ; c3 , x4* c4 ;b
|
Если y f x сложная. То построение графика может быть затруднено. В |
|||||
этом |
случае |
можно |
использовать представление функции в |
виде |
||
f x 1 x 2 x 0 и надо записать 1 x 2 x , |
так чтобы сравнительно просто |
|||||
было |
построить |
графики |
функций |
y 1 x и |
y 2 x . Абсциссы |
точек |
пересечения этих графиков и будут корнями уравнения (8.1) Рис. 8.2. Промежутки изоляции корней можно получать аналитически, используя теоремы о свойствах функций (непрерывных на отрезке).
Уравнение имеет на a; b единственный корень, если
1)функция y f x непрерывна на a; b ;
2)f a f b 0 ;
3)f x сохраняет знак на a; b .
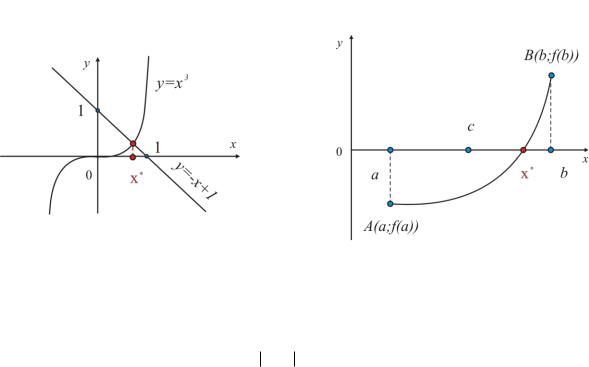
Пример 8.1. Найти изоляции действительных корней уравнения x3 x 1 0 .
Воспользуемся графическим методом отделения корней : построим графики функций y x 3 и y 1 x . Придем к выводу, что корень принадлежит промежутку
[0;1] (Рис. 8.3).
Рис. 8.3 |
Рис. 8.4 |
Уточнение корня. Постанова задачи.
Задача отыскания приближенного значения корня с заданной точностью сводится к нахождению отрезка a; b b a , содержащего только один корень
уравнения (8.1). Эту задачу называют задачей уточнения корня.
Метод половинного деления.
Пусть известно, что a; b |
содержит один единственный корень уравнения |
|
f x 0 |
|||||||||||||||||||||||||||
и |
|
f |
|
a |
|
0, f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
b 0 . Требуется найти его значение с заданной точностью |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
Отрезок |
делим пополам, |
определяем |
точку |
c |
|
|
|
f |
|
c |
|
. Если |
||||||||||||
|
|
|
|
|
|
|
a b / 2 и |
|
|
|
||||||||||||||||||||
f |
|
c |
|
|
0, f |
|
|
|
0 |
то корень |
x |
* |
c;b |
(если f |
|
c |
|
0, f |
|
|
0 , то корень x |
* |
|
a;c ) т.е. |
||||||
|
|
|
b |
|
|
|
|
b |
|
|||||||||||||||||||||
отрезок изоляции корня сузили вдвое (Рис. 8.4).
138
Если b c , то искомый корень уравнения найден с заданной точностью и любое число из c; b можно считать его значением. В противном случае процесс деления пополам можно продолжать.
В методе половинного деления погрешность решения находится в прямой зависимости от числа деления отрезка пополам. При n делениях погрешность равна
b a
2n . Поэтому если произвести достаточно много делений, то искомый корень
можно вычислить с любой степенью точности. Рассмотренный метод удобен еще и тем . что в нем используются однотипные вычисления, поэтому он удобен при реализации вычислений на ЭВМ.
|
|
|
|
Метод хорд. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
Пусть на a; b |
находится единственный корень уравнения f x 0 , |
|||||||||||||||||
f |
|
a |
|
0, f |
|
|
|
|
, |
|
x |
|
сохраняют знак на этом отрезке. Точки A a; f a и |
|||||||||||
|
|
b |
0 и |
f |
x |
f |
|
|||||||||||||||||
B b; f b |
дуги кривой соединим хордой АВ (Рис. 8.5), уравнение которой |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y f a |
|
x a |
|
(8.2) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f b f a |
b a |
|
|||||||
|
|
|
|
Абсцисса |
точки |
пересечения хорды с осью ОХ является первым |
||||||||||||||||||
приближением значения корня x * . Значение x |
1 |
найдем, решив совместно уравнения |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
хорды (8.2) и оси ОХ : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
y f |
a |
|
|
|
x a |
|
|
|
|
f a b a |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
f b f a |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
b a x a |
|
|
|
|
(8.3) |
||||||||||
|
|
|
|
|
|
|
|
|
|
f b f |
a |
|||||||||||||
|
|
|
|
|
|
|
y 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
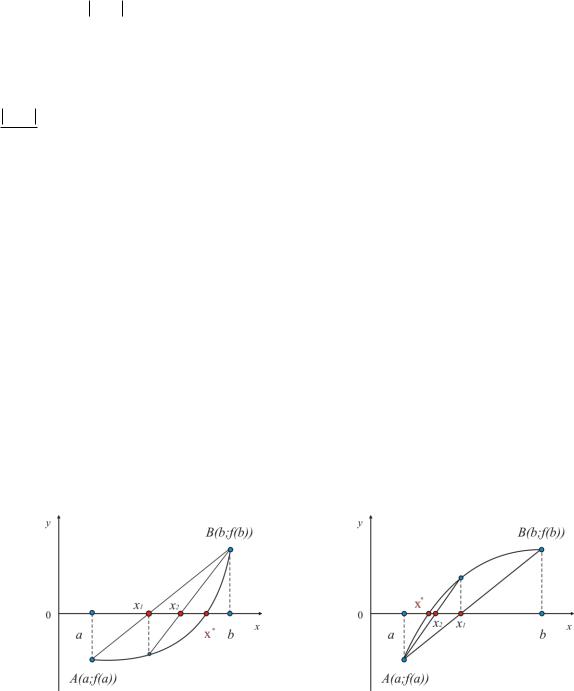
Рис. 8.5 |
|
|
|
|
|
Рис. 8.6 |
Таким образом, получено первое приближение значения корня x1 |
||||||
x a |
f a b a |
|
|
|||
f b f a |
|
|
||||
|
1 |
|
|
|||
|
|
|
|
|
|
|
т.е. получили суженный промежуток |
x1 , b изоляции корня. Применив к нему |
|||||
формулу (8) найдем второе приближение корня |
|
|
||||
x2 x1 |
f |
x1 |
b x1 |
|
|
|
|
|
f x1 |
|
|||
|
|
f |
b |
|||
продолжая этот процесс, получим n-е приближение значения корня уравнения:
